旅行商问题不再难！模拟退火算法的组合优化应用

# 1. 旅行商问题概述

旅行商问题 (TSP) 是一个经典的组合优化问题，它涉及到一个旅行商需要访问一组城市并返回其出发点的最短路径。TSP 在许多实际应用中都有着广泛的应用，例如物流、调度和规划。

TSP 的数学模型可以用图论来表示，其中城市表示为图中的顶点，而城市之间的距离表示为边的权重。旅行商的目标是找到一条哈密顿回路，即访问所有顶点一次并返回出发点的路径，并且该路径的总权重最小。

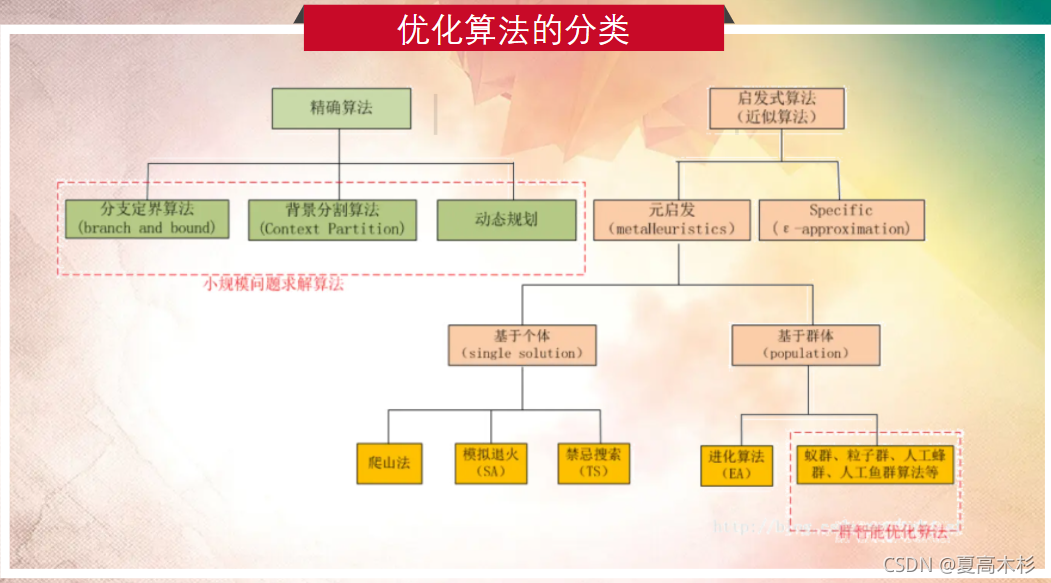
TSP 问题是一个 NP 难问题，这意味着随着城市数量的增加，找到最优解变得非常困难。因此，对于大型 TSP 实例，需要使用启发式算法来获得近似最优解。

# 2. 模拟退火算法理论基础

### 2.1 模拟退火算法的原理和概念

模拟退火算法（Simulated Annealing，SA）是一种受热力学退火过程启发的元启发式算法，用于解决组合优化问题。其基本原理是模拟金属退火的过程，通过不断降低温度，使系统达到能量最低的状态，从而找到问题的最优解。

在模拟退火算法中，系统状态由一组候选解组成，能量函数用于评估解的质量。算法从一个随机初始状态开始，然后通过以下步骤进行迭代：

1. **生成邻域解：**从当前状态生成一个新的候选解，称为邻域解。
2. **计算能量差：**计算新解与当前解之间的能量差 ΔE。
3. **接受或拒绝：**如果 ΔE < 0（新解更好），则接受新解。如果 ΔE ≥ 0（新解更差），则以一定概率接受新解，该概率由温度 T 和 ΔE 决定。

### 2.2 模拟退火算法的数学模型

模拟退火算法的数学模型基于马尔可夫链蒙特卡罗（MCMC）方法。在每个迭代中，系统从当前状态转移到邻域状态的概率由以下公式给出：

P(X_t+1 = x' | X_t = x) = { 1, if ΔE < 0
                            e^(-ΔE/T), if ΔE ≥ 0

其中：

* X_t 是当前状态
* X_t+1 是邻域状态
* ΔE 是能量差
* T 是温度

### 2.3 模拟退火算法的参数和调优

模拟退火算法的关键参数包括：

* **初始温度：**算法开始时的温度，决定了初始接受较差解的概率。
* **降温速率：**温度随迭代次数降低的速度，影响算法收敛速度和解的质量。
* **终止条件：**算法停止的条件，例如达到最大迭代次数或温度降至一定阈值。

参数调优对于模拟退火算法的性能至关重要。可以通过经验法则或自适应方法来优化参数，以平衡探索和利用。

# 3.1 旅行商问题的数学模型

旅行商问题（TSP）是一个经典的组合优化问题，其目标是找到一组城市的最短哈密顿回路，即访问所有城市一次并返回起始城市。TSP 的数学模型可以表示为：

min ∑_{i=1}^{n} ∑_{j=1}^{n} c_{ij} x_{ij}

其中：

* n 是城市的数量
* c_{ij} 是城市 i 到城市 j 的距离
* x_{ij} 是一个二进制变量，表示城市 i 是否直接连接到城市 j

约束条件：

* 对于每个城市 i，∑_{j=1}^{n} x_{ij} = 1
* 对于每个城市 i，∑_{j=1}^{n} x_{ji} = 1
* x_{ii} = 0，对于所有 i

这些约束条件确保每个城市被访问一次，并且回路是哈密顿的。

### 距离矩阵

TSP 的数学模型中，距离矩阵 c_{ij} 是一个 n x n 的矩阵，其中 c_{ij} 表示城市 i 到城市 j 的距离。距离矩阵可以根据实际距离或其他度量标准（例如时间或成本）来构造。

### 哈密顿回路

哈密顿回路是一条经过图中所有顶点一次且不重复的路径。在 TSP 中，哈密顿回路表示访问所有城市一次并返回起始城市的路径。

### 最短哈密顿回路

TSP 的目标是找到最短的哈密顿回路，即总距离最小的回路。最短哈密顿回路问题是一个 NP 难问题，这意味着