物理学中的模拟退火算法：统计力学与量子计算的秘密武器

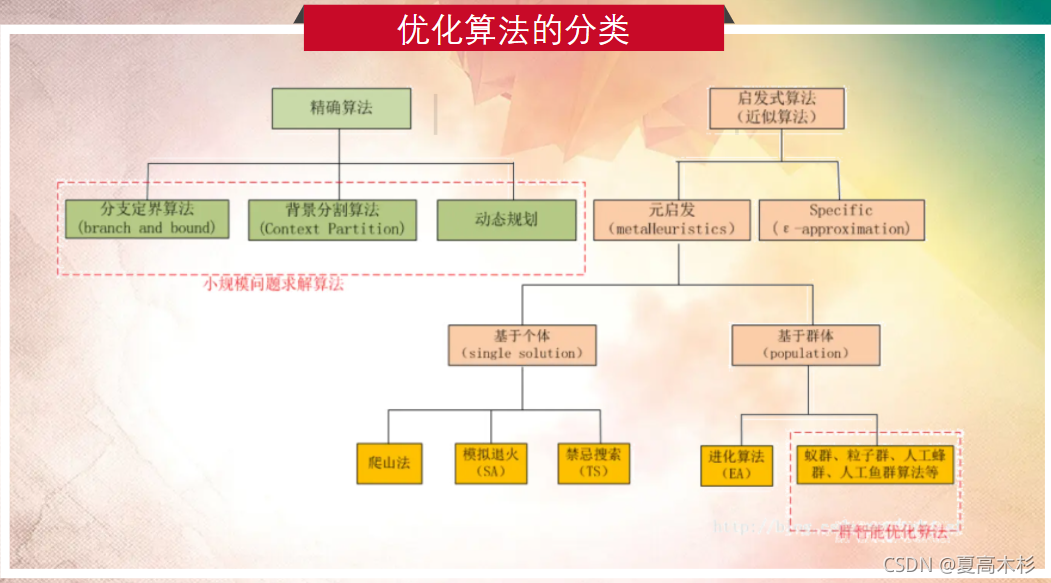
# 1. 模拟退火算法概览**

模拟退火算法是一种概率性全局优化算法，灵感源自于冶金学中金属退火过程。在退火过程中，金属被加热到高温，然后缓慢冷却，使其晶体结构达到最低能量状态。模拟退火算法模拟了这一过程，通过随机搜索和局部优化相结合，寻找复杂优化问题的最优解。

算法的核心思想是允许在搜索过程中暂时接受较差的解，以避免陷入局部最优。通过逐渐降低温度参数，算法逐渐收敛到全局最优解。模拟退火算法适用于解决各种优化问题，包括组合优化、连续优化和物理系统建模。

# 2. 模拟退火算法的理论基础**

**2.1 统计力学原理**

模拟退火算法建立在统计力学原理的基础上，它借鉴了物理系统在热平衡状态下的行为。

**2.1.1 玻尔兹曼分布**

玻尔兹曼分布描述了在热平衡状态下，系统中不同能量状态的粒子分布情况。其公式为：

P(E) = e^(-E/kT) / Z

其中：

* P(E) 是能量为 E 的状态的概率
* E 是能量
* k 是玻尔兹曼常数
* T 是温度
* Z 是配分函数，用于归一化概率分布

**2.1.2 马尔可夫链**

马尔可夫链是一种随机过程，其中一个状态的转移概率仅取决于当前状态，与过去状态无关。模拟退火算法使用马尔可夫链来模拟系统状态的演化。

**2.2 量子计算中的模拟退火**

量子计算为模拟退火算法提供了新的可能性。量子比特可以同时处于多个状态，这使得量子系统能够探索比经典系统更大的搜索空间。

**量子模拟退火算法**

量子模拟退火算法利用量子比特的叠加和纠缠特性来加速模拟退火过程。它通过构建一个量子哈密顿量来表示优化问题，并使用量子退火技术来找到系统的基态，从而获得最优解。

**量子优化算法**

量子优化算法将模拟退火算法与量子计算相结合，以解决复杂优化问题。这些算法利用量子比特的并行性和纠缠性来探索更大的搜索空间，从而找到比经典算法更好的解。

# 3.1 物理学建模与仿真

模拟退火算法在物理学建模与仿真领域有着广泛的应用，特别是在粒子系统和量子系统的模拟中。

#### 3.1.1 粒子系统的模拟

在粒子系统模拟中，模拟退火算法可以用于模拟大量粒子的运动和相互作用。通过定义适当的能量函数，模拟退火算法可以找到粒子的最低能量状态，从而获得系统的稳定结构和性质。

例如，在分子动力学模拟中，模拟退火算法可以用于模拟分子的运动和相互作用，以研究分子的结构和动力学性质。通过定义分子之间的势能函数，模拟退火算法可以找到分子的最低能量构型，从而获得分子的稳定结构。

import numpy as np
import random

# 定义分子之间的势能函数
def potential(r):
    return 4 * (1 / r**12 - 1 / r**6)

# 模拟退火算法
def simulated_annealing(initial_state, temperature, cooling_rate):
    current_state = initial_state
    current_energy = potential(current_state)

    while temperature > 0:
        # 随机扰动当前状态
        new_state = current_state + random.uniform(-1, 1)

        # 计算新状态的能量
        new_energy = potential(new_state)

        # 根据能量差决定是否接受新状态
        if new_energy < current_energy:
            current_state = new_state
            current_energy = new_energy
        else:
            probability = np.exp(-(new_energy - current_energy) / temperature)
            if random.random() < probability:
                current_state = new_state
                current_energy = new_energy

        # 降低温度
        temperature *= cooling_rate

    return current_state

**代码逻辑逐行解读：**

1. 定义分子之间的势能函数 `potential(r)`，其中 `r` 为粒子之间的距离。
2. 定义模拟退火算法函数 `simulated_annealing(initial_state, temperature, cooling_rate)`，其中 `initial_state` 为初始状态，`temperature` 为初始温度，`cooling_rate` 为降温速率。
3. 初始化当前状态 `current_state` 为初始状态，计算其能量 `current_energy`。
4. 进入模拟退火循环，循环条件为温度 `temperature` 大于 0。
5. 随机扰动当前状态，生成新状态 `new_state`。
6. 计算新状态的能量 `new_energy`。
7. 根据能量差决定是否接受新状态：
- 如果 `new_energy` 小于 `current_energy`，则接受新状态，更新 `current_state` 和 `current_energy`。
- 否则，以概率 `probability` 接受新状态，其中 `probability` 根据能量差和当前温度计算