：中点画圆算法在科学可视化中的应用：圆形图表与数据展示，让数据呈现更直观

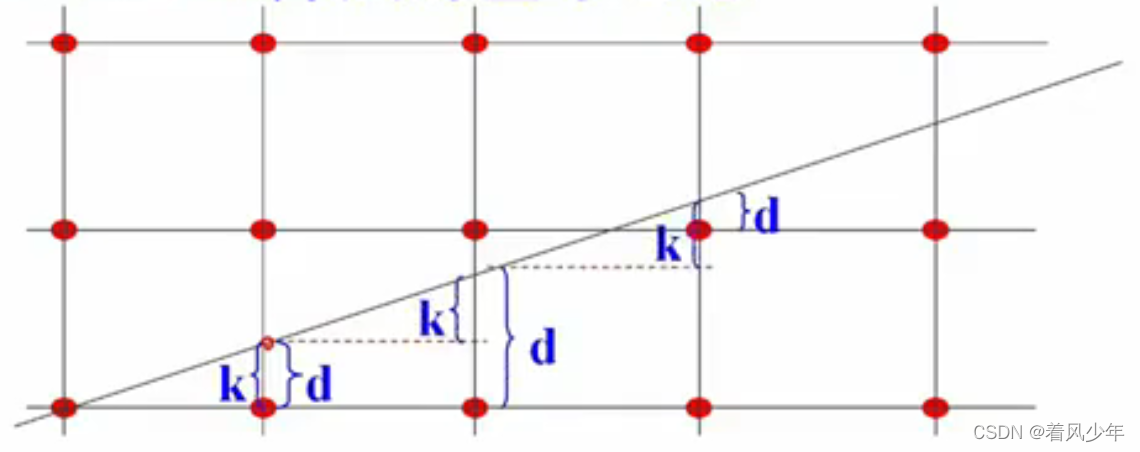
# 1. 中点画圆算法原理与实现

中点画圆算法是一种绘制圆形的经典算法，它利用圆的几何特性和对称性，通过迭代计算圆上各点的坐标，逐步绘制出圆形。

该算法的核心思想是利用圆的对称性，将圆划分为八个对称扇形，从圆心出发，沿圆周以一定的步长移动，计算每个扇形内中点坐标，并绘制出对应的圆弧。通过不断迭代这个过程，最终完成整个圆形的绘制。

# 2. 中点画圆算法在圆形图表中的应用

### 2.1 圆形图表的基本原理

#### 2.1.1 圆形图表的数据结构

圆形图表是一种数据可视化图表，它将数据以扇形区域的形式表示在圆形区域内。每个扇形区域的大小与它所代表的数据值成正比。圆形图表的数据结构通常由一个数组组成，其中每个元素包含一个数据值和一个颜色值。

#### 2.1.2 圆形图表绘制算法

圆形图表绘制算法的基本步骤如下：

1. 计算每个扇形区域的中心角：将总数据值除以 360 度，得到每个扇形区域的中心角。
2. 计算每个扇形区域的起始角和结束角：每个扇形区域的起始角是前一个扇形区域的结束角，第一个扇形区域的起始角为 0 度。
3. 绘制每个扇形区域：根据起始角和结束角，使用中点画圆算法绘制每个扇形区域。

### 2.2 中点画圆算法在圆形图表中的优化

#### 2.2.1 算法效率分析

中点画圆算法在圆形图表中的效率主要受扇形区域数量的影响。随着扇形区域数量的增加，算法的效率会降低。

#### 2.2.2 优化算法实现

为了优化算法实现，可以采用以下方法：

- **预计算三角函数值：**在算法开始时，预计算正弦和余弦函数值，以避免在绘制每个扇形区域时重复计算。
- **使用增量算法：**使用增量算法来计算每个扇形区域的中心角和起始角，以避免使用昂贵的除法和乘法运算。
- **并行化算法：**对于大型圆形图表，可以将算法并行化，以提高效率。

# 优化后的中点画圆算法实现

def draw_circle(x, y, radius, start_angle, end_angle):
    # 预计算三角函数值
    sin_table = [math.sin(angle) for angle in range(0, 360)]
    cos_table = [math.cos(angle) for angle in range(0, 360)]

    # 使用增量算法计算中心角和起始角
    center_angle = (end_angle - start_angle) / 2
    start_angle += center_angle

    # 使用中点画圆算法绘制扇形区域
    x_center = x + radius * cos_table[start_angle]
    y_center = y + radius * sin_table[start_angle]
    for i in range(start_angle, end_angle):
        x_end = x + radius * cos_table[i]
        y_end = y + radius * sin_table[i]
        draw_line(x_center, y_center, x_end, y_end)
        x_center = x_end
        y_center = y_end

**代码逻辑分析：**

1. 预计算三角函数值，存储在 `sin_table` 和 `cos_table` 中。
2. 使用增量算法计算每个扇形区域的中心角和起始角。
3. 使用中点画圆算法绘制扇形区域，使用预计算的三角函数值来提高效率。
4. 循环绘制每个扇形区域，更新圆心坐标。

# 3. 中点画圆算法在数据展示中的应用

### 3.1 数据可视化概述

#### 3.1.1 数据可视化的类型

数据可视化是一种将数据转换为图形、图表