【案例分析】：揭秘PSO-SVM如何在股市预测中大放异彩

# 1. PSO-SVM模型概述与股市预测背景

## 1.1 股市预测的重要性
股市作为全球金融市场的核心部分，不仅影响着企业融资和投资者的投资决策，还关系到宏观经济的稳定与增长。因此，准确预测股市走势对于投资者、政策制定者和经济分析师都具有重要意义。由于股市数据的复杂性和动态性，传统的预测方法往往难以达到理想的效果，这也促使了机器学习技术在股市预测中的应用。

## 1.2 PSO-SVM模型的诞生
为了解决股市预测中的非线性和高维性问题，研究者们将粒子群优化算法（PSO）与支持向量机（SVM）相结合，形成了PSO-SVM模型。PSO是一种群体智能优化技术，具有强大的全局搜索能力和收敛速度快的特点。SVM则是一种有效的分类和回归工具，尤其擅长处理高维数据。通过PSO来优化SVM的参数，可以提升股市预测的准确性和可靠性。

## 1.3 股市预测的新视角
PSO-SVM模型的提出为股市预测提供了新的视角。该模型不仅可以从历史数据中提取有效信息，还能够通过参数的自适应调整，找到最佳的决策边界，从而提高预测的精确度。在接下来的章节中，我们将深入探讨PSO算法与SVM的理论基础，并着重分析PSO-SVM模型在股市预测中的应用。

# 2. PSO算法与SVM理论基础

## 2.1 粒子群优化算法（PSO）基础

### 2.1.1 PSO的起源与发展

粒子群优化（PSO）算法是由Kennedy和Eberhart于1995年提出的一种群体智能优化技术。它的灵感来源于鸟群和社会群体行为的研究，其核心思想是模拟鸟群觅食时的群体搜索行为。在PSO算法中，每个粒子代表问题空间中的一个潜在解。粒子在搜索空间中移动，并通过跟踪个体历史最佳位置与群体历史最佳位置来更新自己的位置和速度。

PSO算法自提出后，因其概念简单、易于实现和调整参数的特点，迅速在优化和搜索领域得到了广泛的应用。经过不断地研究和改进，PSO算法的变种不断涌现，比如带惯性的标准PSO（SPSO）、带收缩因子的PSO（CLPSO）、全局最佳PSO（GPSO）等，这些变种在速度、稳定性和全局搜索能力等方面各有优势。

### 2.1.2 PSO算法的工作原理

PSO算法的工作原理可以通过以下几个步骤来概括：

1. **初始化粒子群**：随机初始化一群粒子的位置和速度。
2. **评估粒子**：根据目标函数评估每个粒子的适应度。
3. **更新个体与全局最佳位置**：每个粒子会记录自己迄今为止找到的最佳位置（个体最佳），整个粒子群中最佳的个体位置即全局最佳位置。
4. **更新速度和位置**：根据个体最佳和全局最佳位置，按照一定的公式来更新粒子的速度和位置。
5. **迭代搜索**：重复步骤2到步骤4，直到满足终止条件（如达到预设的迭代次数或适应度阈值）。

在PSO算法中，粒子的速度更新公式是关键，它通过当前速度、个体最佳位置以及全局最佳位置共同决定。调整这些参数可以控制搜索行为的探索和开发权衡。PSO算法的参数包括惯性权重（inertia weight）、学习因子（cognitive and social coefficients），这些参数对算法的性能有着重要影响。

## 2.2 支持向量机（SVM）理论框架

### 2.2.1 SVM的数学模型和原理

支持向量机（Support Vector Machine，SVM）是一种监督学习模型，用于解决分类和回归问题。SVM的核心思想是通过最优超平面（在高维空间中可能是超曲面）来实现不同类别的分离，这个超平面能够最大化不同类别数据之间的间隔（margin）。这个间隔是指距离超平面最近的数据点与超平面之间的距离。

SVM算法的主要步骤包括：

1. **数据映射**：将原始数据映射到高维特征空间。
2. **计算最优超平面**：在高维空间中求解最优超平面，使得支持向量到该平面的距离之和最大化。
3. **构建分类决策函数**：根据最优超平面构建分类决策函数，用于新数据的分类。

SVM的数学表达式涉及到了拉格朗日乘子法，通过构建拉格朗日函数并引入拉格朗日乘子，可以将原始的有约束优化问题转化为无约束问题。最终，SVM会通过求解对偶问题来得到分类超平面。

### 2.2.2 SVM在分类和回归中的应用

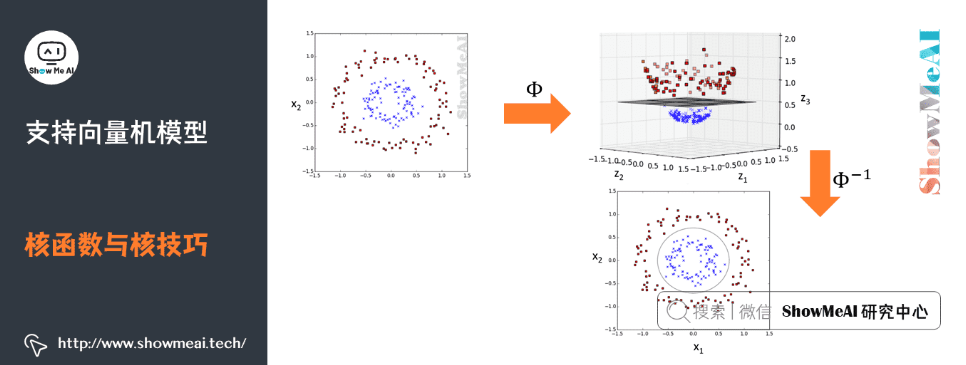
SVM在分类问题中通过寻找最优超平面来实现分类决策，尤其在数据维度高、样本量适中的情况下表现优异。对于非线性问题，SVM可以使用核函数将数据映射到高维空间，从而实现非线性划分。常用核函数包括线性核、多项式核、径向基函数（RBF）核等。

在回归问题中，SVM可以通过支持向量回归（SVR）来处理。SVR的目标是在保持尽可能多的数据点在间隔范围内的同时，最小化间隔边界的偏离程度。这种优化目标使得SVR在预测连续值的问题上具有优势。

## 2.3 PSO与SVM的结合机制

### 2.3.1 PSO用于SVM参数优化的原理

将PSO算法应用于SVM参数优化，主要是针对SVM中的关键参数进行寻优，比如在分类问题中，SVM有两个重要的参数需要调整：正则化参数C和核函数的参数（如RBF核的γ参数）。PSO可以用来寻找这两个参数的最佳组合，以达到最优的分类性能。

PSO算法的群体搜索机制与SVM参数优化问题非常契合。每个粒子代表一组可能的SVM参数，粒子群通过迭代搜索，不断更新个体和全局最佳位置，最终定位到最佳的SVM参数组合。粒子的速度更新与位置更新公式中包含了C和γ参数的调整策略，使得粒子在参数空间中有效搜索。

### 2.3.2 PSO-SVM模型的优势分析

PSO-SVM模型结合了PSO算法的全局搜索能力和SVM出色的分类和回归性能。PSO的全局搜索能力可以帮助SVM避免陷入局部最优解，而SVM的高维数据处理能力使得PSO算法在优化时有更好的收敛速度和准确度。

PSO-SVM模型的优势主要体现在：

- **全局优化**：PSO算法能