【PSO-SVM调参艺术】：专家传授快速找到最佳参数组合的秘诀

# 1. PSO-SVM调参艺术概述

在机器学习和数据挖掘的领域，调参是优化模型性能的关键环节。特别是在使用支持向量机（SVM）进行分类和回归任务时，选择合适的参数至关重要。粒子群优化算法（PSO）是一种群体智能优化技术，它通过模拟鸟群的觅食行为，能够在参数空间中高效搜索最优解。将PSO与SVM结合，形成PSO-SVM模型，可以自动化并智能化地寻找最优的SVM参数组合，这不仅提升了模型的泛化能力，还大幅缩短了参数优化的时间。本章将概述PSO-SVM调参的艺术，介绍其背后的原理和优势，以及在整个调参过程中的重要作用。接下来的章节会深入探讨PSO和SVM的基础理论、实践过程、高级技巧以及未来的发展趋势。

# 2. PSO和SVM的基础理论

### 2.1 SVM核心概念与原理

#### 2.1.1 支持向量机的工作机制
支持向量机（Support Vector Machine，SVM）是一种监督式学习方法，广泛用于分类和回归分析。SVM的基本原理是找到一个能够分割数据集的最优超平面，使得不同类别的数据尽可能地被正确分类，并且与超平面的距离最大化。在二维空间中，这个超平面就是一条线，而在三维空间中则是一个平面，更高维度则是超平面。

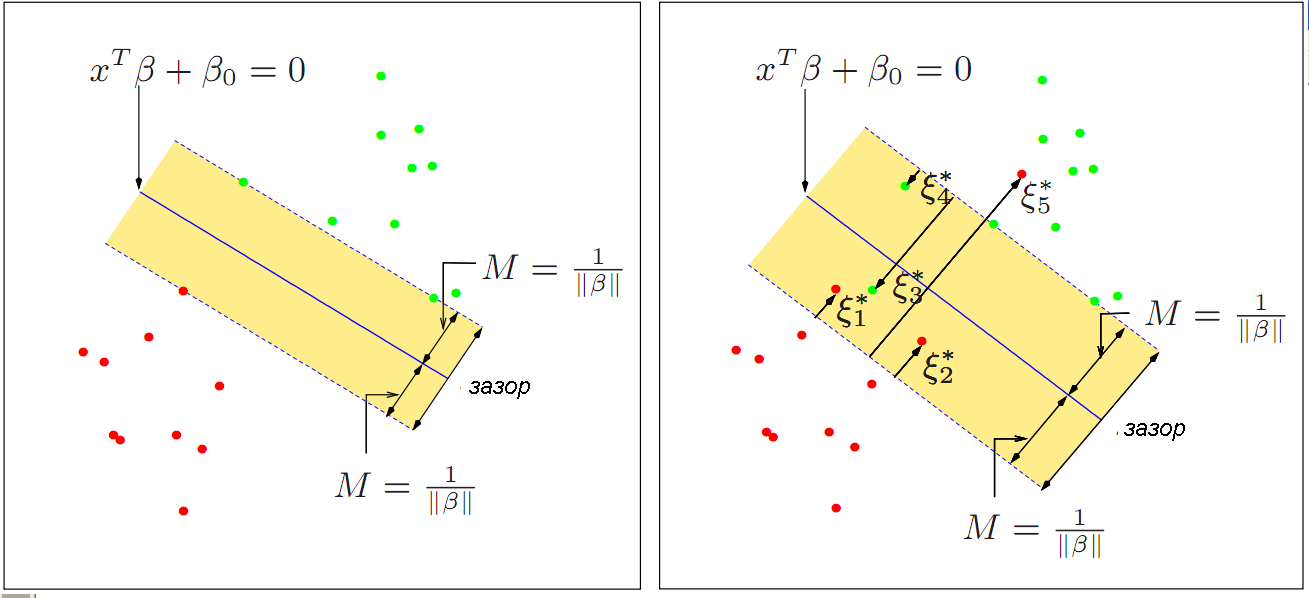
在分类问题中，SVM试图最大化支持向量之间的间隔，也就是最大化两类数据点之间的边界。这个间隔被称为“间隔边界”（margin）。最优超平面就是在保证分类正确性的同时，使得间隔边界最大化。当数据集线性不可分时，SVM通过引入核函数将原始数据映射到高维空间中，使得在新的空间中能够找到一个线性可分的超平面。

SVM的核心是求解一个二次规划问题，即最大化间隔的同时满足每个数据点的约束条件。在数学上，这可以通过拉格朗日乘子法转化为对偶问题求解，从而得到最优的分类超平面。

#### 2.1.2 SVM的损失函数和优化问题
支持向量机的损失函数通常由两部分组成：一部分是经验风险项，用于衡量模型在训练集上的拟合情况；另一部分是结构风险项，用于控制模型的复杂度，防止过拟合。

对于线性可分的数据，SVM的损失函数为：
- 经验风险项：0（因为可以完美分割）
- 结构风险项：通常是最大化间隔，所以是间隔的倒数

对于非线性可分的数据，SVM引入松弛变量（slack variables）ξ，并增加惩罚参数C来控制模型对于误分类点的惩罚程度。此时损失函数变为：
- 经验风险项：Σ(ξ_i)
- 结构风险项：C * Σ(ξ_i) + 间隔的倒数

参数C的引入，为在间隔大小和分类错误之间提供了一种平衡。C值越大，对分类错误的惩罚越重，模型更倾向于减少误分类的数量；C值较小，则模型对间隔的要求更高，但可能会接受更多的分类错误。

对于SVM的优化问题，通常需要解决一个带有不等式约束的二次规划问题。数学上，这通常通过将原始问题转换为对偶问题并使用拉格朗日乘子法来实现。

### 2.2 粒子群优化算法（PSO）介绍

#### 2.2.1 PSO算法基本概念
粒子群优化（Particle Swarm Optimization，PSO）算法是一种基于群体智能的优化算法。PSO模拟鸟群捕食行为，通过群体中个体的协作来寻找最优解。每个个体称为“粒子”，代表着问题空间中的一个潜在解。

粒子通过跟踪个体历史最优解（个体经验）和群体历史最优解（集体经验）来更新自己的位置和速度。粒子的位置代表着潜在的解，而速度则影响着粒子移动的快慢和方向。

PSO算法中，粒子的速度和位置更新公式如下：

v_i^(t+1) = w * v_i^t + c1 * rand() * (pbest_i - x_i^t) + c2 * rand() * (gbest - x_i^t)
x_i^(t+1) = x_i^t + v_i^(t+1)

其中：
- `v_i^(t+1)` 和 `v_i^t` 分别是粒子在t+1和t时刻的速度。
- `x_i^(t+1)` 和 `x_i^t` 分别是粒子在t+1和t时刻的位置。
- `pbest_i` 是粒子个体的历史最佳位置。
- `gbest` 是群体历史最佳位置。
- `w` 是惯性权重，用于控制前一速度对当前速度的影响。
- `c1` 和 `c2` 是学习因子，用于调整粒子向个体经验和社会经验学习的比例。
- `rand()` 是一个在[0,1]范围内的随机数，增加算法的随机性。

#### 2.2.2 PSO算法的数学模型和参数
PSO算法的数学模型是基于迭代的。每一轮迭代中，粒子的位置和速度都会更新，直到满足停止条件（例如达到预设的迭代次数、满足误差阈值等）。

PSO算法的参数包括：
- `w`（惯性权重）：影响粒子的全局搜索能力与局部搜索能力，较大的`w`有利于全局搜索，较小的`w`有利于局部搜索。
- `c1` 和 `c2`（学习因子）：影响粒子个体经验和群体经验的相对重要性，通常取值在[1, 4]之间。
- `rand()`（随机数）：引入随机性，避免陷入局部最优解。
- 粒子数量：影响算法的并行度和收敛速度。

### 2.3 PSO与SVM的结合点

#### 2.3.1 调参问题的重要性
对于支持向量机来说，正确的参数设置对于模型的性能至关重要。这些参数包括正则化参数C、核函数类型（如线性、多项式、径向基函数等），以及核函数的参数（例如RBF核的γ）。参数的选择直接影响模型的复杂度、泛化能力以及计算成本。

手动调参需要大量的试错和经验判断，效率低且容易受到人为因素的影响。自动调参技术的出现，尤其是基于进化算法的参数优化方法，如粒子群优化（PSO），为高效找到SVM最优参数提供了可能。

#### 2.3.2 PSO应用于SVM参数优化的动机
粒子群优化算法作为一种智能优化算法，其对参数空间的搜索能力，使得PSO成为SVM参数优化的自然选择。PSO算法简单、易实现，并且在许多问题上显示出良好的全局搜索能力。

通过PSO优化SVM参数，可以实现自动化和智能化的参数搜索过程，提高找到最优参数组合的效率，从而提升SVM模型的性能。PSO算法通过模拟粒子群的行为，可以在较大的参数空间内寻找到满意的最优解，这在高维、复杂的优化问题中尤为重要。

PSO算法是通过多粒子同时搜索，可以在较短的时间内有效地接近全局最优解，这在