【PSO-SVM进阶玩法】：探索多目标粒子群优化在预测中的应用

# 1. 多目标粒子群优化算法概述

在现代计算领域，优化问题层出不穷，对于存在多个目标需要同时进行优化的问题，传统的单目标优化算法已不能满足需求。多目标粒子群优化（Multi-Objective Particle Swarm Optimization, PSO）算法应运而生，它通过模拟鸟群捕食行为来解决多目标优化问题。该算法在处理复杂问题时，能平衡多个优化目标之间的权衡，以达到最佳的优化效果。

## 1.1 粒子群优化算法的起源与发展

粒子群优化（PSO）是由Kennedy和Eberhart在1995年提出的一种群体智能优化算法。最初的PSO被用于连续函数优化，但随着时间的发展，该算法不断改进并扩展应用到多目标优化领域。

## 1.2 多目标优化的特点与挑战

多目标优化问题的特点是存在多个需要优化的目标函数，而这些目标函数之间可能存在竞争关系，即优化其中一个目标可能会导致另一个目标性能下降。这种优化问题需要寻求一种折衷解，也就是所谓的Pareto最优解。由于多目标问题的解空间和复杂性都大大增加，因此对算法的求解效率、收敛速度及多样性保持等性能提出了更高的挑战。

在下一章中，我们将详细探讨支持向量机（SVM）的基础理论和构建预测模型的具体流程。

# 2. SVM基础与预测模型构建

## 2.1 支持向量机（SVM）理论基础

### 2.1.1 SVM的核心概念与原理

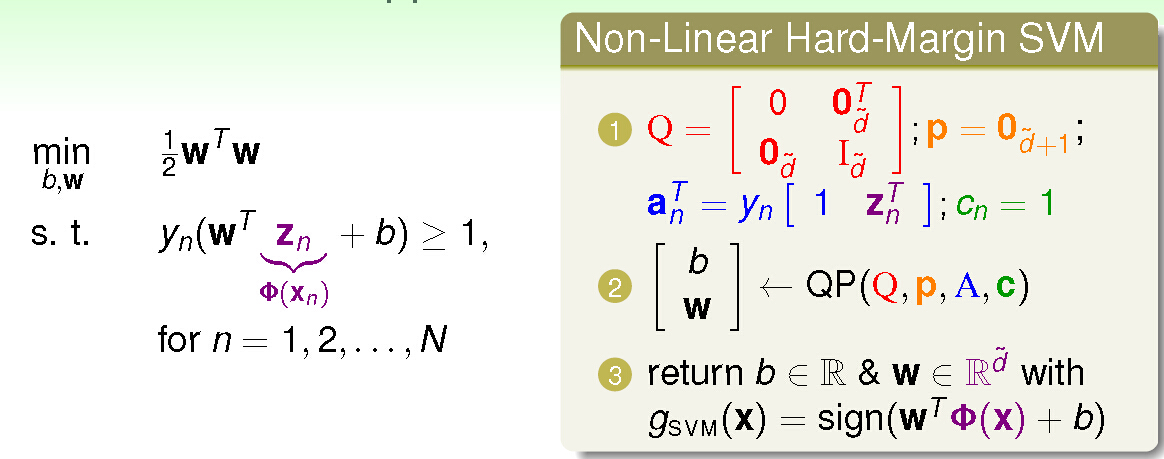
支持向量机（Support Vector Machine, SVM）是一种广泛用于模式识别和回归分析的监督学习算法。它的核心思想是找到一个最优的超平面，以最大化不同类别之间的边界，也就是最大化边缘（margin）。在二维空间中，这个超平面就是一个直线，而在更高维的空间中，它就是一个超平面或者超曲面。

SVM 通过解决以下优化问题来求解分类决策函数：

minimize: 1/2 ||w||^2
subject to: y_i (w . x_i + b) >= 1, i = 1, ..., n

其中，x_i 表示训练样本，y_i 表示对应的类别标签（+1 或 -1），w 是超平面的法向量，b 是偏置项。||w||^2 是 L2 范数，用于控制模型的复杂度。

### 2.1.2 SVM在分类与回归中的应用

SVM在分类问题中有着出色的表现，尤其在处理高维数据和非线性问题时表现突出。通过引入核技巧（kernel trick），SVM能够有效地处理非线性分类问题。核函数允许在高维空间中计算内积，而无需显式地进行空间变换，从而实现了所谓的“核化”（kernelization）。

在回归问题中，SVM可以扩展为支持向量回归（Support Vector Regression, SVR）。其主要思想是在保证预测误差可接受的前提下，尽可能最大化数据点与决策函数之间的间隔。通过调整惩罚参数和损失函数，SVR能够有效控制模型的复杂度与对异常值的敏感度。

## 2.2 SVM预测模型的构建流程

### 2.2.1 数据预处理与特征选择

构建一个有效的SVM模型的第一步是进行适当的数据预处理。这包括数据清洗、缺失值处理、数据标准化等步骤。数据标准化对于SVM特别重要，因为模型对输入特征的规模非常敏感。

特征选择是机器学习中非常关键的一步，它涉及到从原始特征中选取最有信息量的特征子集。在SVM模型构建中，特征选择可以提高模型的训练效率，并且有助于避免过拟合。

### 2.2.2 模型参数调优与验证

SVM模型的性能高度依赖于参数的选择，特别是惩罚参数C和核函数参数。参数调优通常采用交叉验证（cross-validation）的方法，以确保模型在未见数据上有良好的泛化能力。

常用的参数调优方法有网格搜索（grid search），它通过对参数空间进行穷举搜索，找到最优的参数组合。在实际应用中，也可以考虑使用随机搜索（random search）或者贝叶斯优化（Bayesian optimization）等方法，它们在处理高维参数空间时更加高效。

from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC

# 假设已经有了训练数据和标签
X_train = ... # 训练数据
y_train = ... # 训练标签

# 设置SVM模型
svc = SVC()

# 设置网格搜索参数
parameters = {'C': [1, 10, 100], 'gamma': [0.001, 0.01, 0.1], 'kernel': ['rbf', 'linear']}

# 进行网格搜索
clf = GridSearchCV(svc, parameters, cv=5)
clf.fit(X_train, y_train)

# 输出最佳参数组合
print(clf.best_params_)

该代码段展示了如何使用`GridSearchCV`对SVM的C、gamma和kernel参数进行网格搜索，以找到最佳的模型参数组合。在网格搜索过程中，将采用5折交叉验证来评估不同参数组合的性能。

### SVM模型的构建与参数调优逻辑分析

在上述代码中，我们首先导入了`GridSearchCV`和`SVC`类。`SVC`类是scikit-learn中实现SVM分类器的类，而`GridSearchCV`类则用于自动执行网格搜索以及交叉验证。

参数字典`parameters`定义了需要优化的超参数及其取值范围。在本例中，我们优化了C（正则化参数）、gamma（核函数参数）以及kernel（核函数类型）三个参数。

接下来，创建`GridSearchCV`实例时，传入了`SVC`的实例、参数字典以及交叉验证的折数。调用`fit`方法后，`GridSearchCV`会自动完成对所有参数组合的搜索，并找出交叉验证性能最好的模型。

最后，我们通过`clf.best_params_`获取最佳的参数组合并打印出来。该组合是经过网格搜索和交叉验证后，认为最能够提高模型性能的参数配置。

通过参数调优，我们可以得到一个优化后的SVM模型，它在给定的数据集上具有更好的泛化能力。在实际应用中，我们还可以进一步分析模型的错误分类情况，通过特征重要性分析、混淆矩阵等方法评估模型的性能。

# 3. 多目标粒子群优化在SVM中的实现

## 3.1 粒子群优化（PSO）基本原理

### 3.1.1 PSO的数学模型与算法流程

粒子群优化算法（Particle Swarm Optimization, PSO）是一种基于群体智能的优化技术，由Kennedy和Eberhart于1995年提出。PSO模拟鸟群捕食的行为，通过群体中个体的合作与竞争来完成复杂空间中的搜索问题。

PSO算法中，每个粒子代表问题空间中的一个潜在解。每个粒子都具有位置(position)和速度(velocity)两个属性，并且根据自己的经验和群体的经验更新这两个属性。粒子的个体经验是指该粒子曾经达到的最佳位置，群体经验是指所有粒子曾经达到的最佳位置，通常称为全局最优位置(gbest)。

PSO的数学模型如下：
- 速度更新方程：
\[
v_{i}^{(t+1)} = w \cdot v_{i}^{(t)} + c_1 \cdot rand() \cdot (pbest_{i} - x_{i}^{(t)}) + c_2 \cdot rand() \cdot (gbest - x_{i}^{(t)})
\]
- 位置更新方程：
\[
x_{i}^{(t+1)} = x_{i}^{(t)} + v_{i}^{(t+1)}
\]
其中：
- \(v_{i}^{(t)}\) 是第 \(t\) 次迭代中粒子 \(i\) 的速度。
- \(x_{i}^{(t)}\) 是第 \(t\) 次迭代中粒子 \(i\) 的位置。
- \(pbest_{i}\) 是粒子 \(i\) 的最佳位置。
- \(gbest\) 是群体中所有粒子的最佳位置。
- \(w\) 是惯性权重，控制速度的更新幅度。
- \(c_1\) 和 \(c_2\) 是加速系数，分别代表个体和群体经验对速度的影响。
- \(rand()\) 产生一个[0,1]范围内的随机数。

算法流程可以简述为：
1. 初始化粒子群中每个粒子的位置和速度。
2. 评估每个粒子的适应度。
3. 更新每个粒子的个体最佳位置 \(pbest\) 和全局最佳位置 \(gbest\)。
4. 根据速度更新方程调整粒子的速度。
5. 根据位置更新方程调整粒子的位置。
6. 重复步骤2至5，直至满足终止条件（如达到最大迭代次数或者解的质量满足要求）。

### 3.1.2 PSO在优化问题中的应用案例

PSO作为一种强大的全局优化算法，已被广泛应用于各种工程和科学问题中，例如函数优化、神经网络训练、调度问题以