【自编码器网络结构设计】

# 1. 自编码器的理论基础

## 神经网络与编码概念
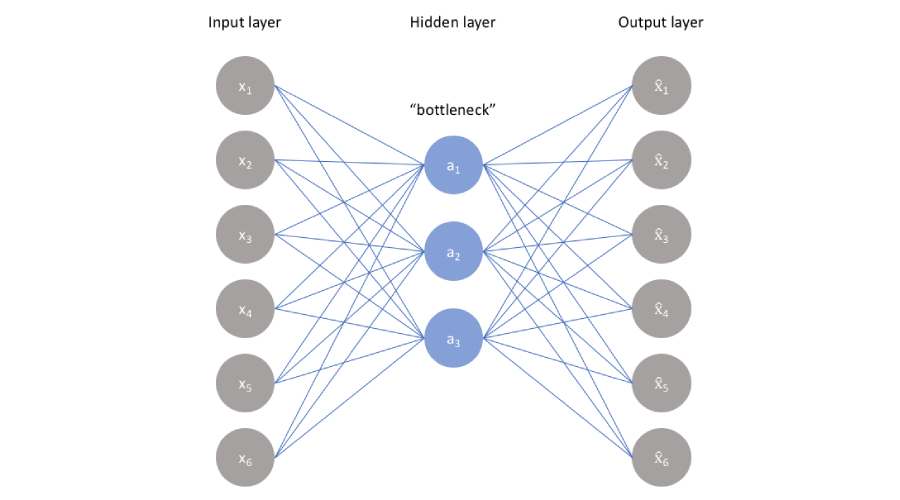
自编码器（Autoencoder，AE）是一种无监督的深度学习模型，主要用于数据的有效编码和降维。其核心思想是通过一个编码过程将输入数据转换为隐藏表示，再通过解码过程重构原始输入数据。自编码器由编码器（encoder）和解码器（decoder）两部分组成，其训练过程是端到端的。

## 理想的自编码器
理想情况下，自编码器能够学习输入数据的重要特征，压缩并重构出与原数据尽可能相似的输出。如果自编码器被设计为仅学习数据的主特征，它可以被用作特征提取器或在降维任务中使用。

## 自编码器的数学表达
数学上，自编码器可以被看作是通过编码函数\( h=f(x) \)将输入\( x \)映射到一个低维表示\( h \)，然后通过解码函数\( r=g(h) \)将这个表示重新映射回重构输入\( r \)。训练过程中，目标是最小化原始输入\( x \)和重构输入\( r \)之间的差异，这通常通过最小化损失函数来实现。

接下来，我们将探索自编码器的不同类型及其原理，以便更好地理解其在各类问题中的应用。

# 2. 自编码器的主要类型及其原理

自编码器是一种特殊的神经网络，它通过学习数据的高效编码来实现特征的提取和数据的压缩。自编码器的基本结构通常包含一个编码器（encoder）和一个解码器（decoder）。编码器将输入数据转换为一个中间的表示（也称为编码或潜在空间表示），而解码器则将这个表示还原为接近原始输入数据的输出。自编码器在无监督学习中被广泛应用，它不仅可以用于降维、特征提取，还可以用于异常检测和生成模型等领域。

### 2.1 基础自编码器

#### 2.1.1 线性自编码器

线性自编码器是最基础的自编码器类型，它的编码器和解码器都使用线性变换。形式上，如果输入数据为x，编码函数为f，解码函数为g，则编码器可以表示为编码c = f(x) = Wx + b1，解码器可以表示为输出y = g(c) = W'c + b2，其中W和W'为权重矩阵，b1和b2为偏置项。线性自编码器的学习目标是最小化输入数据x与输出y之间的差异，通常使用均方误差（MSE）作为损失函数。

线性自编码器由于其简单性，在理解自编码器的基本工作原理方面非常有用，但它的表达能力有限，通常只在数据具有线性特征时使用。

| 类型        | 描述                                                         |
| ----------- | ------------------------------------------------------------ |
| 线性自编码器 | 使用线性变换进行编码和解码，表达能力有限，适用于数据具有线性特征的情况。 |

graph LR
    A[输入数据x] -->|线性变换| B[编码c]
    B -->|线性变换| C[输出y]
    C --> D[损失计算]

#### 2.1.2 非线性自编码器

非线性自编码器在编码器和解码器中引入了非线性激活函数，如sigmoid或ReLU。非线性自编码器能够捕捉输入数据中的非线性结构，因此具有更强的表达能力。非线性自编码器的编码函数和解码函数分别可以表示为c = f(x) = σ(Wx + b1)和y = g(c) = σ(W'c + b2)，其中σ表示非线性激活函数。

| 类型          | 描述                                                         |
| ------------- | ------------------------------------------------------------ |
| 非线性自编码器 | 通过引入非线性激活函数，使得编码器和解码器能够捕捉数据中的非线性特征，具有更强的表达能力。 |

### 2.2 正则化自编码器

正则化自编码器在损失函数中引入了正则项，以防止模型过拟合并提高泛化能力。常见的正则化自编码器包括稀疏自编码器、噪声自编码器和去噪自编码器。

#### 2.2.1 稀疏自编码器

稀疏自编码器通过在损失函数中加入稀疏惩罚项，鼓励模型学习到具有稀疏性的表示。稀疏惩罚项通常可以表示为一个L1正则项或者是Kullback-Leibler散度，用来对编码表示中的激活程度进行约束。稀疏自编码器特别适合于特征提取和数据表示学习。

| 类型        | 描述                                                         |
| ----------- | ------------------------------------------------------------ |
| 稀疏自编码器 | 在损失函数中加入稀疏惩罚项，鼓励编码表示具有稀疏性，适用于特征提取和数据表示学习。 |

#### 2.2.2 噪声自编码器

噪声自编码器通过给输入数据添加噪声，迫使网络学习到更加鲁棒的特征表示。噪声的添加可以是有结构的，也可以是随机的，这样网络在学习过程中就不得不忽略噪声的影响，专注于学习数据的本质特征。

| 类型        | 描述                                                         |
| ----------- | ------------------------------------------------------------ |
| 噪声自编码器 | 通过向输入数据添加噪声，迫使网络学习更鲁棒的特征表示，特别适用于数据噪声较多的情况。 |

#### 2.2.3 去噪自编码器

去噪自编码器是噪声自编码器的一个变种，它在训练阶段向输入数据添加噪声，但在损失函数中仍以原始无噪声数据作为目标。去噪自编码器通过训练网络恢复原始数据，从而学会数据的内在结构，常用于数据降噪和特征提取。

| 类型        | 描述                                                         |
| ----------- | ------------------------------------------------------------ |
| 去噪自编码器 | 在训练时向输入数据添加噪声，但以原始数据为目标，训练网络恢复原始数据，适用于数据降噪和特征提取。 |

### 2.3 卷积自编码器

卷积自编码器利用卷积神经网络（CNN）的架构，特别适用于处理图像数据。卷积层能够提取图像的局部特征，通过堆叠多个卷积层可以逐步提取更加复杂的特征。

#### 2.3.1 基于卷积的自编码器架构

基于卷积的自编码器架构通常包括卷积编码器和转置卷积解码器。卷积编码器通过卷积层、池化层逐渐降低数据的空间维度，并提取特征；转置卷积解码器则通过转置卷积层（也称为反卷积层）、上采样层逐步恢复原始图像的空间维度。

| 类型          | 描述                                                         |
| ------------- | ------------------------------------------------------------ |
| 卷积自编码器 | 利用卷积神经网络架构处理图像数据，通过卷积层提取特征，并通过转置卷积层恢复图像空间维度。 |

#### 2.3.2 应用于图像数据的卷积自编码器

在图像处理任务中，卷积自编码器可以用于图像的降噪、去模糊、特征提取等。例如，用于医学图像处理时，卷积自编码器可以有效地去除噪声，提取出更清晰的图像特征，辅助医生进行诊断。

| 应用场景     | 描述                                                         |
| ------------ | ------------------------------------------------------------ |
| 医学图像处理 | 利用卷积自编码器去除噪声，提取清晰的图像特征，辅助医生进行诊断。 |

### 2.4 变分自编码器

变分自编码器（VAE）是一种生成模型，它通过引入潜在变量来学习数据的概率分布。VAE使用随机编码器和确定性解码器的结构，将输入数据映射到潜在空间中，并能从潜在空间中采样来生成新的数据实例。

#### 2.4.1 变分自编码器的基本概念

VAE的基本思想是将数据生成过程看作是从潜在空间中的随机变量采样得到的过程。编码器学习将数据映射到潜在空间的分布参数（如均值和方差），而解码器则根据这些分布参数生成数据。VAE引入了重参数化技巧（reparameterization trick），使得梯度可以通过潜在空间传播，从而可以使用反向传播算法进行训练。

| 类型        | 描述                                                         |
| ----------- | ------------------------------------------------------------ |
| 变分自编码器 | 作为一种生成模型，通过引入潜在变量学习数据的概率分布，特别适用于数据生成任务。 |

#### 2.4.2 变分自编码器与生成对抗网络

变分自编码器与生成对抗网络（GAN）都是生成模型，但它们的工作原理和训练方式有所不同。GAN通过训练一个生成器和一个判别器来生成数据，而VAE则是通过学习数据的概率分布来生成数据。VAE在生成数据的多样性上可能不如GAN，但VAE提供了一种更加明确的概率框架，使得数据生成的质量更容易控制。

| 类型          | 描述                                                         |
| ------------- | ------------------------------------------------------------ |
| VAE与GAN对比  | VAE提供明确的概率框架，易于控制生成质量，而GAN在生成数据多样性上表现更好。 |

通过本章的介绍，我们对自编码器的主要类型及其原理有了深入的了解，下一章我们将探讨自编码器的损失函数选择与优化策略。

# 3. 自编码器的损失函数与优化策略

自编码器（Autoencoder）是一种广泛应用于无监督学习领域的神经网络模型，其核心目标是通过学习一个能够有效地将输入数据映射到自身（或近似自身）的编码表示，来完成特征提取或数据压缩的任务。为了使模型能够捕捉到数据的本质特征，损失函数和优化策略的选择至关重要。