【自编码器优化秘籍】

# 1. 自编码器的基础概念和应用

## 自编码器简介
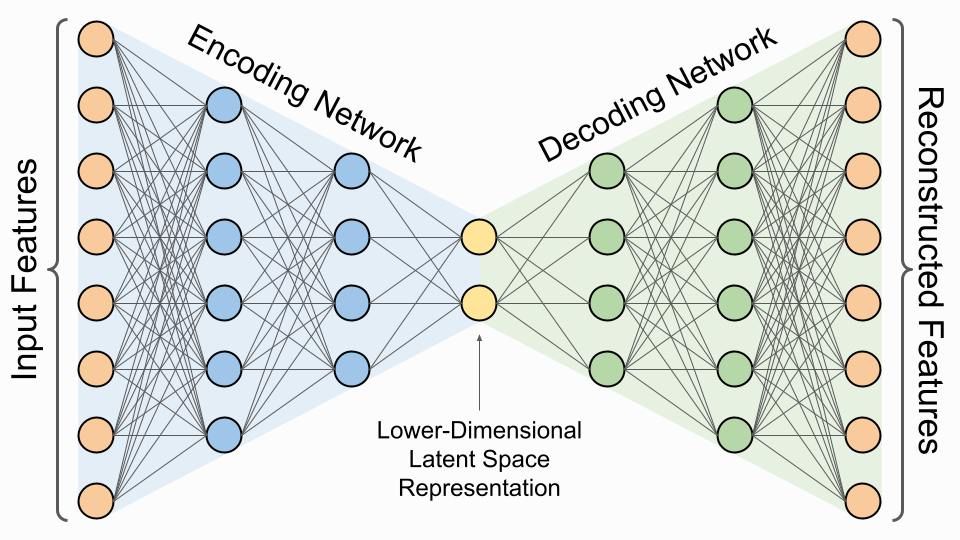
自编码器（Autoencoder）是一种神经网络，其主要目的是通过学习数据的压缩表示来还原输入本身。这种机制的核心思想是迫使神经网络学习到一种更高效的数据表示，即编码，从而可以忽略无关特征，只关注数据的关键信息。

## 自编码器的应用场景
自编码器广泛应用于降维、特征学习、数据去噪等领域。例如，在图像处理中，自编码器可用于消除图像噪声，保留关键信息；在无监督学习中，它可以作为生成模型的一部分，用于数据生成和增强。

## 自编码器的典型结构
基本自编码器结构包括编码器和解码器两部分。编码器负责将输入数据压缩成低维表示，而解码器则将这个表示重构回原始数据。实践中，自编码器可能还会使用稀疏性、正则化等技术以提高性能。

# 2. 自编码器的理论基础

### 2.1 自编码器的数学原理

#### 2.1.1 线性代数基础

自编码器的核心数学原理建立在线性代数之上，其中涉及到矩阵运算、向量空间以及特征分解等概念。线性代数是处理自编码器中权重矩阵和输入输出向量的基础工具。矩阵运算包括矩阵乘法、转置以及特征值和特征向量的求解，这些都是理解自编码器如何对数据进行编码和解码的关键。

自编码器通常用到的线性代数运算中，矩阵乘法是最重要的操作之一。假设我们有输入向量 `\( x \)`, 和编码器权重矩阵 `\( W \)`, 则编码向量 `\( z \)` 可以通过如下方式得到：

z = W.dot(x)

这里 `\( W \)` 是一个 `\( m \times n \)` 的矩阵，其中 `\( m \)` 是编码向量的维度，`\( n \)` 是输入向量的维度。

另一个重要的概念是特征分解。在自编码器中，我们经常需要对权重矩阵 `\( W \)` 进行特征分解，这有助于我们理解矩阵的性质和对数据压缩或降维的效果。特征值和特征向量的计算对于理解自编码器的隐层表示至关重要。

为了理解特征分解的过程，我们使用如下的Python代码进行示例：

import numpy as np

# 假设W是我们要分解的矩阵
W = np.array([[1.1, 0.5], [0.5, 1.3]])

# 对W进行特征分解
eigenvalues, eigenvectors = np.linalg.eig(W)

在上述代码中，`eigenvalues` 和 `eigenvectors` 分别是矩阵 `\( W \)` 的特征值和特征向量。这些特征向量指明了数据变化的主要方向，而特征值则说明了相应方向的方差大小，这为我们提供了数据的内在结构信息。

#### 2.1.2 优化理论简介

自编码器在训练过程中，核心是优化问题，即寻找最优的参数以最小化损失函数。优化理论涉及到了如何系统地选择参数，以使得模型在给定任务上表现最佳。在自编码器的上下文中，这通常意味着最小化输入数据和通过编码器和解码器网络重构后的输出之间的差异。

常用的优化算法包括梯度下降法、随机梯度下降法（SGD）以及其变种。梯度下降的核心思想是通过计算损失函数相对于网络参数的梯度，然后在梯度的反方向上更新参数，以期达到局部最小值。

例如，如果 `\( \mathcal{L} \)` 是损失函数，`\( \theta \)` 是模型参数，一个简单的SGD更新规则可以表示为：

# 假设梯度已经计算出来
gradients = compute_gradients(loss_function, parameters)

# 参数更新
***ters = parameters - learning_rate * gradients

其中 `\( \text{learning_rate} \)` 是学习率，控制着参数更新的步伐大小。

优化理论还包括了正则化技术，如L1和L2正则化，以防止模型过拟合。正则化可以被看作是优化过程中对损失函数的一个附加项，它惩罚模型复杂度，引导模型学习更为平滑的函数。

### 2.2 自编码器的结构和类型

#### 2.2.1 基本自编码器

基本自编码器由编码器（encoder）和解码器（decoder）两部分组成。编码器将输入数据映射到一个低维表示，而解码器则从这个低维表示中恢复出原始数据。在数学上，如果 `\( x \)` 是输入数据， `\( f \)` 是编码器函数，`\( g \)` 是解码器函数，那么基本自编码器的整个过程可以表示为：

z = f(x)
x_reconstructed = g(z)

在实际应用中，`\( f \)` 和 `\( g \)` 往往通过多层神经网络实现。例如，在Python中使用Keras框架来构建一个简单的自编码器模型，代码如下：

from keras.layers import Input, Dense
from keras.models import Model

# 编码器
input_img = Input(shape=(input_dim,))
encoded = Dense(encoding_dim, activation='relu')(input_img)

# 解码器
decoded = Dense(input_dim, activation='sigmoid')(encoded)

# 自编码器模型
autoencoder = Model(input_img, decoded)

在这段代码中，`encoding_dim` 是编码层的维度，它小于输入数据的维度 `input_dim`。在编码器和解码器中，我们使用了激活函数 `relu` 和 `sigmoid`，它们在非线性映射中起到关键作用。

#### 2.2.2 变分自编码器

变分自编码器（VAE）是一种基于概率生成模型的自编码器。不同于传统自编码器，VAE通过引入潜在空间的概率分布来生成新的数据样本。VAE的编码器部分学习将输入数据映射到潜在空间的参数（通常是均值和方差），而解码器则基于这些参数生成数据。

VAE的关键概念是潜在变量，其分布通常假设为高斯分布。在训练过程中，VAE利用重参数化技巧和 KL 散度来使得潜在空间的分布更加接近标准高斯分布，从而达到更好的数据生成效果。

下面是一个简单的VAE模型的代码实现：

from keras.layers import Lambda, Input, Dense
from keras.models import Model
from keras import backend as K

# 定义输入层
inputs = Input(shape=(input_dim,))

# 定义编码器
encoded = Dense(intermediate_dim, activation='relu')(inputs)
z_mean = Dense(latent_dim)(encoded)
z_log_sigma = Dense(latent_dim)(encoded)

# 重参数化过程
def sampling(args):
    z_mean, z_log_sigma = args
    batch = K.shape(z_mean)[0]
    dim = K.int_shape(z_mean)[1]
    epsilon = K.random_normal(shape=(batch, dim))
    return z_mean + K.exp(0.5 * z_log_sigma) * epsilon

z = Lambda(sampling, output_shape=(latent_dim,), name='z')([z_mean, z_log_sigma])

# 定义解码器
decoded = Dense(intermediate_dim, activation='relu')(z)
decoded_output = Dense(input_dim, activation='sigmoid')(decoded)

# 构建VAE模型
autoencoder = Model(inputs, decoded_output)

在这段代码中，`z_mean` 和 `z_log_sigma` 分别表示潜在空间均值和对数方差。`sampling` 函数通过从均值和方差定义的高斯分布中采样，来生成潜在变量 `z`。

#### 2.2.3 对抗性自编码器

对抗性自编码器引入了对抗性网络的训练机制，通过引入一个判别器来区分原始数据和重构数据。这种自编码器的训练过程类似于生成对抗网络（GAN），判别器和自编码器的编码器相互竞争，提升模型的性能。

编码器试图生成使得判别器无法区分的样本，而判别器则尽可能地鉴别出这些样本。这个过程类似于一个零和游戏，编码器和判别器在这个过程中不断优化，直到达到平衡点。

下面是一个简单对抗性自编码器的代码示例：

from keras.layers import Input, Dense, Lambda, Flatten, Reshape
from keras.models import Model
from keras.layers import BatchNormalization, LeakyReLU
from keras.datasets import mnist
import numpy as np

# 载入数据并预处理
(x_train, _), (x_test, _) = mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = np.expand_dims(x_train, axis=-1)
x_test = np.expand_dims(x_test, axis=-1)
x_t