稀疏矩阵在增强现实中的应用：融合现实与虚拟，创造全新体验

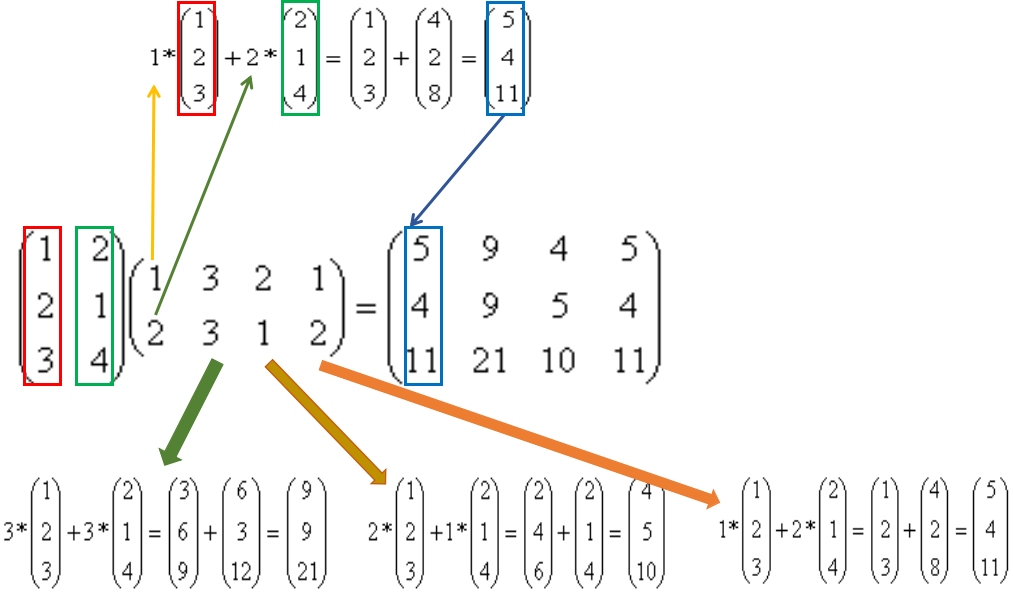
# 1. 稀疏矩阵简介

稀疏矩阵是一种特殊类型的矩阵，其元素大部分为零。在增强现实（AR）中，稀疏矩阵被广泛用于表示场景几何结构、运动轨迹等数据。

稀疏矩阵的存储格式主要有坐标存储格式和行索引存储格式。坐标存储格式直接存储非零元素的坐标和值，而行索引存储格式则存储每个非零元素的行索引和值。稀疏矩阵的运算主要包括加减法和乘法，其中乘法运算需要考虑稀疏性特点进行优化。

# 2. 稀疏矩阵在增强现实中的理论基础

### 2.1 稀疏矩阵的表示和存储

稀疏矩阵是一种特殊类型的矩阵，其中大部分元素为零。在增强现实中，稀疏矩阵被广泛用于表示场景几何结构、运动轨迹等数据，具有节省存储空间、提高计算效率的优势。

#### 2.1.1 坐标存储格式

坐标存储格式是最简单的稀疏矩阵存储方式，它将非零元素及其坐标存储在一个列表中。对于一个稀疏矩阵 A，其坐标存储格式如下：

[(i1, j1, v1), (i2, j2, v2), ..., (in, jn, vn)]

其中，(i, j)表示非零元素在矩阵中的行和列索引，v表示非零元素的值。

**优点：**

- 存储空间占用少，仅存储非零元素。
- 查找和访问非零元素方便。

**缺点：**

- 矩阵加减法运算效率低。
- 矩阵乘法运算效率低，需要遍历所有元素。

#### 2.1.2 行索引存储格式

行索引存储格式将矩阵的每一行非零元素的列索引和值存储在一个列表中。对于一个稀疏矩阵 A，其行索引存储格式如下：

[
    (j1, v1), (j2, v2), ..., (jn, vn)   // 第一行非零元素
    (j1, v1), (j2, v2), ..., (jn, vn)   // 第二行非零元素
    ...
    (j1, v1), (j2, v2), ..., (jn, vn)   // 第m行非零元素
]

**优点：**

- 矩阵加减法运算效率高。
- 矩阵乘法运算效率高，可以利用稀疏矩阵的特性进行优化。

**缺点：**

- 存储空间占用稍大，需要存储所有非零元素的列索引。
- 查找和访问非零元素相对麻烦。

### 2.2 稀疏矩阵的运算

稀疏矩阵的运算与普通矩阵类似，但由于其稀疏性，需要采用特殊的算法来提高效率。

#### 2.2.1 加减法

稀疏矩阵的加减法运算非常简单，只需对非零元素进行逐个加减即可。

def sparse_matrix_add(A, B):
    """稀疏矩阵加法运算"""
    C = {}
    for (i, j, v) in A.items():
        if (i, j) in B:
            C[(i, j)] = v + B[(i, j)]
        else:
            C[(i, j)] = v
    for (i, j, v) in B.items():
        if (i, j) not in C:
            C[(i, j)] = v
    return C

#### 2.2.2 乘法

稀疏矩阵的乘法运算需要考虑稀疏矩阵的特性，采用特殊算法来提高效率。常用的算法包括：

- **坐标存储格式乘法：**遍历两个矩阵的所有非零元素，计算对应位置的乘积并累加。
- **行索引存储格式乘法：**利用行索引存储格式的特性，将乘法转化为一系列稀疏向量的加法运算。

def sparse_matrix_multiply(A, B):
    """稀疏矩阵乘法运算"""
    C = {}
    for (i, j, v) in A.items():
        for (k, l, w) in B.items():
            if j == k:
                if (i, l) in