稀疏矩阵在图像处理中的应用：揭秘图像处理的幕后功臣

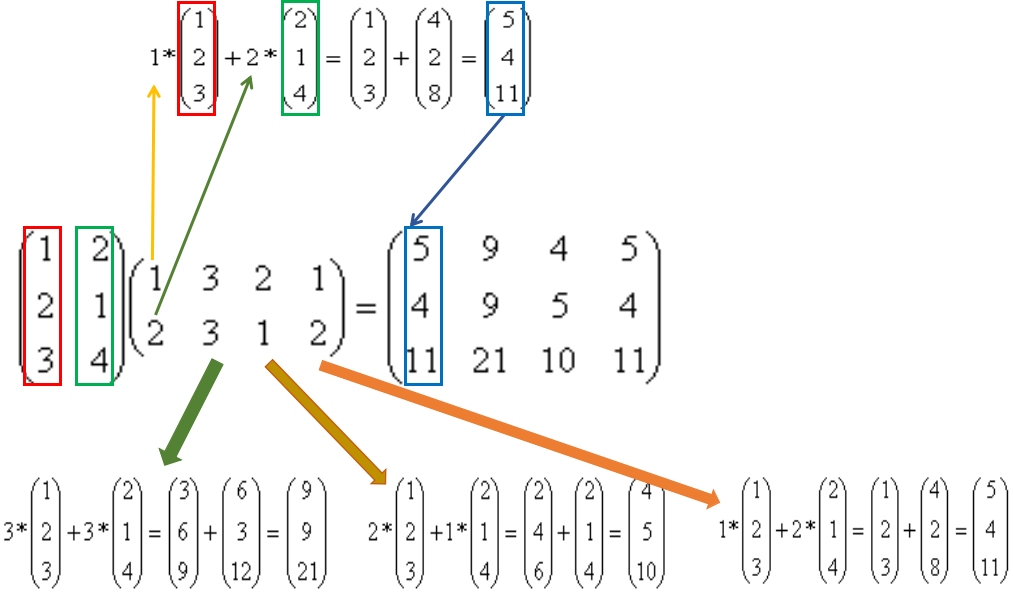
# 1. 稀疏矩阵概述**

稀疏矩阵是一种特殊的矩阵，其元素中大部分为零。在图像处理领域，稀疏矩阵广泛应用于图像表示和算法中。稀疏矩阵的存储和操作与传统矩阵不同，需要采用专门的格式和算法。

稀疏矩阵的存储格式主要有坐标格式、CSR格式和CSC格式。这些格式通过只存储非零元素及其位置来节省空间。稀疏矩阵的运算也需要专门的算法，例如稀疏矩阵的加减法、乘法和转置。

# 2. 稀疏矩阵在图像处理中的应用**

稀疏矩阵在图像处理中扮演着至关重要的角色，因为它能够有效地表示和处理图像数据中的稀疏性。图像通常包含大量零值，而稀疏矩阵可以利用这一特性来节省存储空间和计算时间。

### 2.1 图像表示中的稀疏性

数字图像本质上是稀疏的，因为图像中通常只有少数像素具有非零值。例如，一张黑白图像可以表示为一个二值矩阵，其中 0 表示黑色像素，1 表示白色像素。对于一张 1000x1000 的图像，只有大约 0.1% 的像素是非零的。

### 2.2 稀疏矩阵在图像处理算法中的应用

稀疏矩阵在图像处理算法中有着广泛的应用，包括：

#### 2.2.1 图像压缩

图像压缩算法利用稀疏性来减少图像文件的大小。通过使用稀疏矩阵存储图像数据，可以只存储非零值及其位置，从而显著减少存储空间。常用的图像压缩格式，如 JPEG 和 PNG，都利用了稀疏矩阵的原理。

#### 2.2.2 图像增强

稀疏矩阵还可以用于图像增强算法。例如，可以通过稀疏矩阵表示图像梯度，并利用梯度信息进行边缘检测和锐化。稀疏矩阵的稀疏性可以加速梯度计算，从而提高算法效率。

#### 2.2.3 图像分割

图像分割算法将图像分割成不同的区域。稀疏矩阵可以用于表示图像中的区域邻接关系，并利用稀疏矩阵的运算进行区域合并和分割。稀疏矩阵的稀疏性可以减少计算复杂度，提高分割算法的效率。

**代码示例：**

import numpy as np
from scipy.sparse import csr_matrix

# 创建一个稀疏矩阵表示的图像
image = np.array([[0, 1, 0],
                   [1, 1, 1],
                   [0, 1, 0]])

# 将图像转换为 CSR 稀疏矩阵
sparse_image = csr_matrix(image)

# 打印稀疏矩阵
print(sparse_image)

**逻辑分析：**

这段代码使用 NumPy 和 SciPy 库创建了一个稀疏矩阵表示的图像。`csr_matrix` 函数将图像转换为 CSR 格式的稀疏矩阵，该格式是图像处理中常用的稀疏矩阵存储格式。

**参数说明：**

* `image`: 要转换为稀疏矩阵的图像数组。
* `csr_matrix`: SciPy 中的 CSR 稀疏矩阵类。

**表格：稀疏矩阵在图像处理中的应用**

| 应用 | 描述 |
|---|---|
| 图像压缩 | 利用稀疏性减少图像文件大小 |
| 图像增强 | 使用稀疏矩阵表示梯度信息进行边缘检测和锐化 |
| 图像分割 | 利用稀疏矩阵表示区域邻接关系进行区域合并和分割 |

# 3. 稀疏矩阵的存储与操作

### 3.1 稀疏矩阵的存储格式

稀疏矩阵的存储格式决定了其在内存中如何表示，不同的存储格式具有不同的空间和时间复杂度。常见的稀疏矩阵存储格式包括：

#### 3.1.1 坐标格式

坐标格式是最简单的稀疏矩阵存储格式，它使用三个数组存储矩阵中的非零元素：

* 行索引数组：存储非零元素所在的行号
* 列索引数组：存储非零元素所在的列号
* 值数组：存储非零元素的值

import numpy as np

# 创建一个稀疏矩阵
matrix = np.array([[0, 0, 1], [0, 2, 3], [4, 0, 5]])

# 转换为坐标格式
row_indices, col_indices, values = matrix.nonzero()

# 打印坐标格式
print("行索引数组：", row_indices)
print("列索引数组：", col_indices)
print("值数组：", values)

**参数说明：**

* `matrix.nonzero()`: 返回一个元组，包含三个数组：行索引数组、列索引数组和值数组。

**代码逻辑：**

该代码将稀疏矩阵转换为坐标格式，并打印出三个数组的内容。

#### 3.1.2 CSR格式

CSR（Compressed Sparse Row）格式是一种压缩行存储格式，它使用三个数组存储矩阵中的非零元素：

* 值数组：存储非零元素的值
* 行指针数组：存储每行的第一个非零元素在值数组中的位置
* 列索引数组：存储非零元素所在的列号

import scipy.sparse as sp

# 创建一个稀疏矩阵
matrix = sp.csr_matrix([[0, 0, 1], [0, 2, 3], [4, 0, 5]])

# 获取 CSR 格式的数组
data = matrix.data
indptr = matrix.indptr
indices = matrix.indices

# 打印 CSR 格式
print("值数组：", data)
print("行指针数组：", indptr)
print("列索引数组：", indices)

**参数说明：**

* `matrix.data`: 返回值数组。
* `matrix.indptr`: 返回行指针数组。
* `matrix.indices`: 返回列索引数组。

**代码逻辑：**

该代码将稀疏矩阵转换为 CSR 格式，并打印出三个数组的内容。

#### 3.1.3 CSC格式

CSC（Compressed Sparse Column）格式是一种压缩列存储格式，它使用三个数组存储矩阵中的非零元素：

* 值数组：存储非零元素的值
* 列指针数组：存储每列的第一个非零元素在值数组中的位置
* 行索引数组：存储非零元素所在的行号

import scipy.sparse as sp

# 创建一个稀疏矩阵
matrix = sp.csc_matrix([[0, 0, 1], [0, 2, 3], [4, 0, 5]])

# 获取 CSC 格式的数组
data = matrix.data
indptr = matrix.indptr
indices = matrix.indices

# 打印 CSC 格式
print("值数组：", data)
print("列指针数组：", indptr)
print("行索引数组：", indices)

**参数说明：**

* `matrix.data`: 返回值数组。
* `matrix.indptr`: 返回列指针数组。
* `matrix.indices`: 返回行索引数组。

**代码逻辑：**

该代码将稀疏矩阵转换为 CSC 格式，并打印出三个数组的内容。

### 3.2 稀疏矩阵的运算

稀疏矩阵的运算与稠密矩阵的运算类似，但由于稀疏矩阵的特殊性，需要采用特定的算法和优化技术。

#### 3.2.1 加减法

稀疏矩阵的加减法运算相对简单，直接对非零元素进行加减即可。

import numpy as np

# 创建两个稀疏矩阵
matrix1 = np.array([[0, 0, 1], [0, 2, 3], [4, 0, 5]])
matrix2 = np.array([[0, 0, 2], [0, 3, 4], [5, 0, 6]])

# 加法运算
matrix_sum = matrix1 + matrix2

# 减法运算
matrix_diff = matrix1 - matrix2

# 打印运算结果
print("加法运算结果：")
print(matrix_sum)
print("减法运算结果：")
print(matrix_diff)

**代码逻辑：**

该代码创建了两个稀疏矩阵，并对它们进行加法和减法运算，打印出运算结果。

#### 3.2.2 乘法

稀疏矩阵的乘法运算需要使用特定的算法，例如稀疏矩阵-向量乘法（SpMV）和稀疏矩阵-稀疏矩阵乘法（SpMM）。

import scipy.sparse as sp

# 创建两个稀疏矩阵
matrix1 = sp.csr_matrix([[0, 0, 1], [0, 2, 3], [4, 0, 5]])
matrix2 = sp.csr_matrix([[0, 0, 2], [0, 3, 4], [5, 0, 6]])

# 稀疏矩阵-向量乘法
vector = np.array([1, 2, 3])
result_vector = matrix1.dot(vector)

# 稀疏矩阵-稀疏矩阵乘法
result_matrix = matrix1.dot(matrix2)

# 打印运算结果
print("稀疏矩阵-向量乘法结果：")
print(result_vector)
print("稀疏矩阵-稀疏矩阵乘法结果：")
print(result_matrix)

**参数说明：**

* `matrix1.dot(vector)`: 执行稀疏矩阵-向量乘法。
* `matrix1.dot(matrix2)`: 执行稀疏矩阵-稀疏矩阵乘法。

**代码逻辑：**

该代码创建了两个稀疏矩阵，并对它们执行稀疏矩阵-向量乘法和稀疏矩阵-稀疏矩阵乘法，打印出运算结果。

#### 3.2.3 转置

稀疏矩阵的转置运算需要使用特定的算法，例如转置自由树（Transpose-Free Tree）算法。

import scipy.sparse as sp

# 创建一个稀疏矩阵
matrix = sp.csr_matrix([[0, 0, 1], [0, 2, 3], [4, 0, 5]])

# 转置运算
transposed_matrix = matrix.transpose()

# 打印转置结果
print("转置结果：")
print(transposed_matrix)

**参数说明：**

* `matrix.transpose()`: 执行稀疏矩阵的转置运算。

**代码逻辑：**

该代码创建了一个稀疏矩阵，并对它执行转置运算，打印出转置结果。

# 4. 稀疏矩阵在图像处理中的优化

### 4.1 稀疏矩阵的压缩

稀疏矩阵的压缩旨在减少其存储空间需求，同时保持其数学性质。压缩算法可分为两类：无损压缩和有损压缩。

#### 4.1.1 无损压缩

无损压缩算法不改变稀疏矩阵的数值，从而保证了压缩后的矩阵与原始矩阵在数学上等价。常用的无损压缩算法包括：

- **行索引压缩 (RLE)**：将连续的非零元素的行索引编码为一个值和一个长度。
- **列索引压缩 (CLE)**：与 RLE 类似，但针对列索引进行编码。
- **混合压缩 (HC)**：结合 RLE 和 CLE，同时压缩行和列索引。

#### 4.1.2 有损压缩

有损压缩算法允许对稀疏矩阵的数值进行近似，从而进一步减少存储空间需求。常用的有损压缩算法包括：

- **奇异值分解 (SVD)**：将稀疏矩阵分解为三个矩阵的乘积，其中一个矩阵包含奇异值。奇异值可以被截断以减少矩阵的大小。
- **随机投影 (RP)**：将稀疏矩阵投影到一个低维子空间，从而减少其维度。
- **哈希表压缩 (HTC)**：使用哈希表存储非零元素，并使用哈希函数将元素映射到一个较小的空间。

### 4.2 稀疏矩阵的并行处理

稀疏矩阵的并行处理可以利用多核处理器或图形处理器 (GPU) 的并行性，从而提高图像处理算法的性能。常用的并行处理技术包括：

#### 4.2.1 OpenMP 并行化

OpenMP 是一种共享内存并行编程模型，允许在多核处理器上并行执行代码。对于稀疏矩阵操作，OpenMP 可以用于并行化循环和矩阵-向量乘法。

#### 4.2.2 CUDA 并行化

CUDA 是一种基于 GPU 的并行编程模型，允许在 GPU 上执行代码。对于稀疏矩阵操作，CUDA 可以用于并行化矩阵-向量乘法、矩阵-矩阵乘法和矩阵转置。

### 4.2.3 并行稀疏矩阵-向量乘法

稀疏矩阵-向量乘法是图像处理中常用的操作。并行稀疏矩阵-向量乘法算法包括：

- **CSR 并行算法**：使用 CSR 格式存储稀疏矩阵，并使用 OpenMP 或 CUDA 并行化循环。
- **CSC 并行算法**：使用 CSC 格式存储稀疏矩阵，并使用 OpenMP 或 CUDA 并行化循环。
- **Block CSR 并行算法**：将 CSR 格式的稀疏矩阵划分为块，并使用 OpenMP 或 CUDA 并行化块之间的操作。

### 4.2.4 并行稀疏矩阵-矩阵乘法

稀疏矩阵-矩阵乘法是图像处理中另一个常用的操作。并行稀疏矩阵-矩阵乘法算法包括：

- **CSR-CSR 并行算法**：使用 CSR 格式存储两个稀疏矩阵，并使用 OpenMP 或 CUDA 并行化循环。
- **CSC-CSC 并行算法**：使用 CSC 格式存储两个稀疏矩阵，并使用 OpenMP 或 CUDA 并行化循环。
- **Block CSR-CSC 并行算法**：将 CSR 格式的稀疏矩阵划分为块，将 CSC 格式的稀疏矩阵划分为列块，并使用 OpenMP 或 CUDA 并行化块之间的操作。

# 5.1 图像去噪

稀疏矩阵在图像去噪中发挥着至关重要的作用。图像去噪旨在去除图像中的噪声，提高图像质量。

### 稀疏表示和字典学习

图像去噪的一个常见方法是稀疏表示和字典学习。该方法假设图像可以表示为一个稀疏向量，该向量由一个过完备字典中的基向量线性组合而成。

import numpy as np
from sklearn.decomposition import SparseCoder

# 加载图像
image = ...

# 训练字典
dictionary = SparseCoder(dictionary_size=100)
dictionary.fit(image)

# 稀疏表示
sparse_representation = dictionary.transform(image)

### 去噪过程

利用稀疏表示，图像去噪过程如下：

1. **稀疏表示：**将图像表示为一个稀疏向量。
2. **阈值化：**将稀疏向量中的小系数阈值化，保留大的系数。
3. **重建：**使用阈值化后的稀疏向量和字典重建图像。

# 阈值化
thresholded_representation = np.where(np.abs(sparse_representation) > threshold, sparse_representation, 0)

# 重建
denoised_image = dictionary.inverse_transform(thresholded_representation)

### 优势

稀疏矩阵在图像去噪中的优势包括：

* **有效性：**稀疏表示可以有效地去除噪声，同时保留图像的细节。
* **效率：**稀疏矩阵的运算比稠密矩阵的运算更有效率。
* **可扩展性：**稀疏矩阵的并行处理可以提高图像去噪的效率。