稀疏矩阵在人工智能中的应用：推动人工智能的突破性进展

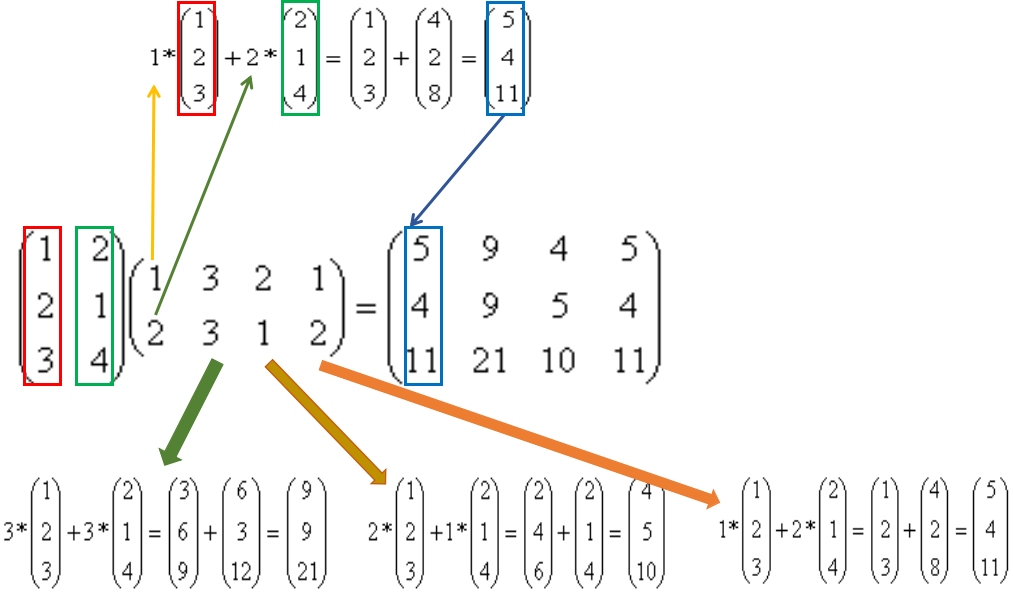
# 1. 稀疏矩阵概述

稀疏矩阵是一种特殊类型的矩阵，其元素中大部分为零。在实际应用中，稀疏矩阵非常常见，例如在机器学习、计算机视觉和自然语言处理等领域。稀疏矩阵的处理和存储与稠密矩阵不同，需要专门的算法和数据结构。

本章将介绍稀疏矩阵的基本概念、特性和存储方式。稀疏矩阵的存储方式主要有两种：坐标格式和压缩格式。坐标格式简单易懂，但存储效率较低；压缩格式存储效率高，但操作复杂。

# 2. 稀疏矩阵在人工智能中的理论基础

### 2.1 稀疏矩阵的特性和表示

#### 2.1.1 稀疏矩阵的定义和特点

稀疏矩阵是一种特殊类型的矩阵，其中大多数元素为零。与稠密矩阵（所有元素均非零）相比，稀疏矩阵具有以下特点：

- **存储效率高：**由于大多数元素为零，因此稀疏矩阵可以仅存储非零元素，从而节省存储空间。
- **计算效率高：**在许多操作（如矩阵乘法）中，稀疏矩阵的计算量远低于稠密矩阵，因为可以跳过对零元素的计算。

#### 2.1.2 稀疏矩阵的存储方式

有几种方法可以存储稀疏矩阵，包括：

- **坐标列表 (COO)：**存储非零元素的行列索引和值。
- **压缩行存储 (CSR)：**存储每个行的非零元素的列索引和值，以及每个行的非零元素数量。
- **压缩列存储 (CSC)：**存储每个列的非零元素的行索引和值，以及每个列的非零元素数量。

### 2.2 稀疏矩阵的数学运算

#### 2.2.1 稀疏矩阵的加减法

稀疏矩阵的加减法操作与稠密矩阵类似，但由于稀疏矩阵的非零元素较少，因此计算量更低。

def sparse_matrix_add(A, B):
    """
    对两个稀疏矩阵进行加法操作。

    参数：
        A：稀疏矩阵 A
        B：稀疏矩阵 B

    返回：
        稀疏矩阵 C，为 A 和 B 的和
    """
    # 检查矩阵尺寸是否匹配
    if A.shape != B.shape:
        raise ValueError("矩阵尺寸不匹配")

    # 创建稀疏矩阵 C
    C = sp.lil_matrix(A.shape)

    # 遍历矩阵 A 和 B 的非零元素
    for i, j, v in zip(A.row, A.col, A.data):
        C[i, j] += v

    for i, j, v in zip(B.row, B.col, B.data):
        C[i, j] += v

    return C

#### 2.2.2 稀疏矩阵的乘法

稀疏矩阵的乘法操作与稠密矩阵不同，因为需要考虑非零元素的分布。

def sparse_matrix_multiply(A, B):
    """
    对两个稀疏矩阵进行乘法操作。

    参数：
        A：稀疏矩阵 A
        B：稀疏矩阵 B

    返回：
        稀疏矩阵 C，为 A 和 B 的乘积
    """
    # 检查矩阵尺寸是否匹配
    if A.shape[1] != B.shape[0]:
        raise ValueError("矩阵尺寸不匹配")

    # 创建稀疏矩阵 C
    C = sp.lil_matrix((A.shape[0], B.shape[1]))

    # 遍历矩阵 A 的行
    for i in range(A.shape[0]):