稀疏矩阵在计算机视觉中的应用：赋能计算机视觉的强大工具

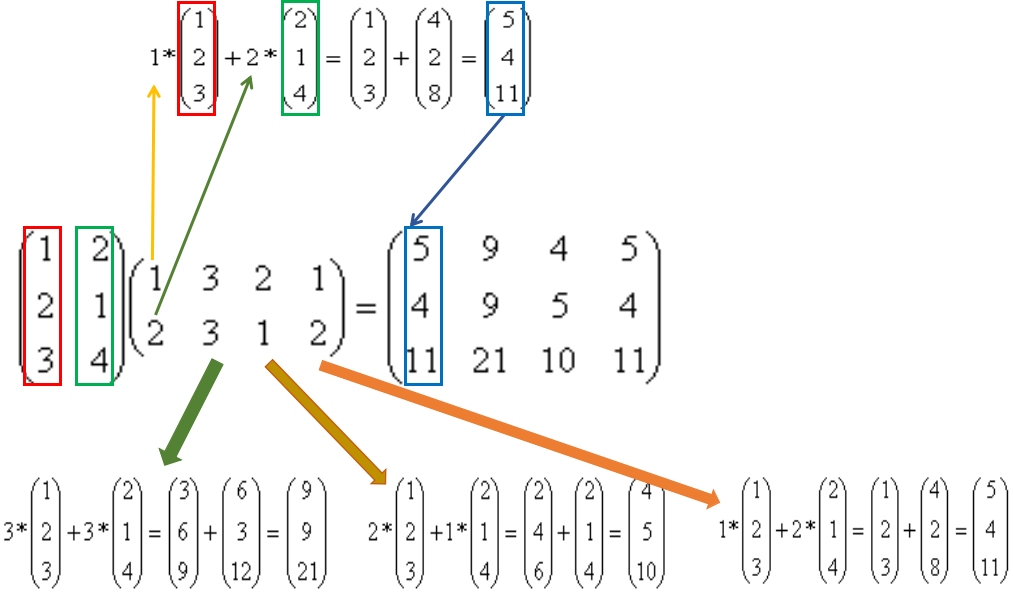
# 1. 稀疏矩阵概述**

稀疏矩阵是一种特殊类型的矩阵，其中大多数元素为零。在计算机视觉等领域，稀疏矩阵经常用于表示图像或视频数据，因为这些数据通常具有大量的零值。

稀疏矩阵的优点包括：

- **存储效率：** 由于大多数元素为零，因此稀疏矩阵可以比普通矩阵更有效地存储。
- **计算效率：** 由于零值元素不需要参与计算，因此稀疏矩阵的计算可以比普通矩阵更快。

# 2. 稀疏矩阵的计算机视觉应用

### 2.1 图像分割

#### 2.1.1 基于图论的图像分割

基于图论的图像分割将图像表示为一个图，其中像素作为节点，相邻像素之间的连接作为边。通过对图进行分割，可以得到图像的不同区域。

**代码块：**

import networkx as nx

# 创建图
G = nx.Graph()
# 添加节点
for i in range(width):
    for j in range(height):
        G.add_node((i, j))
# 添加边
for i in range(width):
    for j in range(height):
        if i < width - 1:
            G.add_edge((i, j), (i + 1, j))
        if j < height - 1:
            G.add_edge((i, j), (i, j + 1))

# 分割图像
communities = nx.community.greedy_modularity_communities(G)

**逻辑分析：**

* `networkx`库用于创建和操作图。
* `nx.Graph()`创建了一个无向图。
* `add_node()`和`add_edge()`用于向图中添加节点和边。
* `nx.community.greedy_modularity_communities()`使用贪心算法根据模块度对图进行分割。

#### 2.1.2 基于聚类的图像分割

基于聚类的图像分割将图像中的像素聚合成不同的簇，每个簇代表图像中的一个区域。

**代码块：**

import numpy as np
from sklearn.cluster import KMeans

# 提取图像特征
features = ...

# 聚类
kmeans = KMeans(n_clusters=k)
kmeans.fit(features)

# 分割图像
segmented_image = np.zeros_like(image)
for i in range(width):
    for j in range(height):
        segmented_image[i, j] = kmeans.labels_[i * width + j]

**逻辑分析：**

* `numpy`库用于处理图像数据。
* `sklearn.cluster.KMeans`用于进行K均值聚类。
* `fit()`方法将聚类算法应用于图像特征。
* `labels_`属性包含每个像素所属的簇标签。
* 循环遍历图像像素并根据簇标签设置分割后的图像。

### 2.2 目标检测

#### 2.2.1 基于滑窗的目标检测

基于滑窗的目标检测在图像上滑动一个窗口，并对每个窗口进行分类，以判断窗口内是否包含目标。

**代码块：**

for i in range(width - window_size):
    for j in range(height - window_size):
        window = image[i:i + window_size, j:j + window_size]
        score = classifier.predict(window)
        if score > threshold:
            # 检测到目标
            ...

**逻辑分析：**

* 循环遍历图像窗口。
* `classifier.predict()`方法对窗口进行分类，返回目标存在的概率。
* 如果概率大于阈值，则检测到目标。

#### 2.2.2 基于区域建议的目标检测

基于区域建议的目标检测使用预先训练的模型生成候选区域，然后对这些区域进行分类和回归，以获得目标的精确位置。

**流程图：**

graph LR
subgraph 建议区域生成
    start-->init_model
    init_model-->extract_features
    extract_features-->generate_proposals
end
subgraph 目标检测
    start-->load_model
    load_model-->classify_proposals
    classify_proposals-->regress_proposals
end

**参数说明：**

* `init_model`：初始化区域建议模型。
* `extract_features`：提取图像特征。
* `generate_proposals`：生成候选区域。
* `load_model`：加载目标检测模型。
* `classify_proposals`：对候选区域进行分类。
* `regress_proposals`：对候选区域进行回归，获得目标的精确位置。

### 2.3 运动跟踪

#### 2.3.1 基于卡尔曼滤波的运动跟踪

基于卡尔曼滤波的运动跟踪使用卡尔曼滤波器预测目标的位置和速度，并通过与观测值进行更新来提高预测的准确性。

**代码块：**