稀疏矩阵在生物信息学中的应用：探索生命科学中的数据奥秘

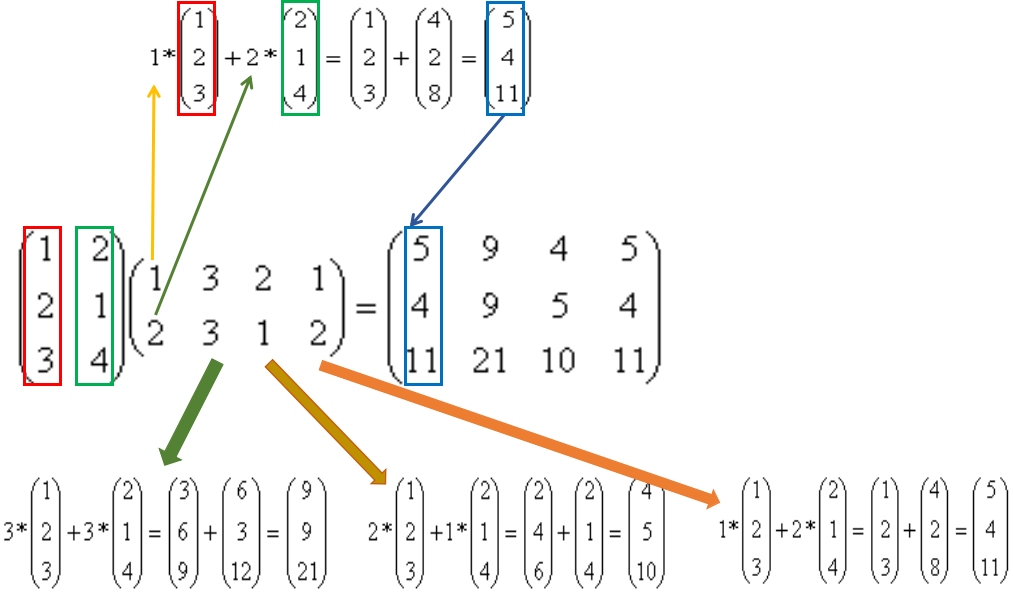
# 1. 稀疏矩阵简介**

稀疏矩阵是一种特殊类型的矩阵，其元素中大多数为零。在实际应用中，稀疏矩阵非常常见，例如图像处理、基因组学和网络分析等领域。稀疏矩阵的存储和计算与普通矩阵不同，需要专门的算法和数据结构。

稀疏矩阵的存储格式通常采用坐标格式或压缩行存储格式。坐标格式直接存储非零元素的位置和值，而压缩行存储格式通过存储每行非零元素的起始位置和长度来压缩存储空间。稀疏矩阵的计算方法主要包括直接乘法算法和快速傅里叶变换算法。直接乘法算法直接计算稀疏矩阵的乘积，而快速傅里叶变换算法通过将稀疏矩阵转换为稠密矩阵来提高计算效率。

# 2. 稀疏矩阵在生物信息学中的应用**

稀疏矩阵在生物信息学中有着广泛的应用，主要集中在基因表达分析和蛋白质组学分析两个方面。

## 2.1 基因表达分析

### 2.1.1 微阵列数据分析

微阵列技术是一种高通量基因表达分析技术，它可以同时检测数千个基因的表达水平。微阵列数据通常以稀疏矩阵的形式存储，其中行表示基因，列表示样品，非零元素表示基因在该样品中的表达水平。

**代码块 1：微阵列数据稀疏矩阵**

import numpy as np

# 创建一个稀疏矩阵来表示微阵列数据
data = np.array([[0, 0, 1],
                  [0, 1, 0],
                  [1, 0, 0]])
sparse_matrix = scipy.sparse.csr_matrix(data)

# 打印稀疏矩阵
print(sparse_matrix)

**逻辑分析：**

* `scipy.sparse.csr_matrix` 函数用于创建压缩行存储 (CSR) 格式的稀疏矩阵。
* CSR 格式是一种稀疏矩阵的存储格式，它将非零元素的行索引、列索引和值分别存储在三个数组中。
* 打印稀疏矩阵时，它将以以下格式显示：

   (0, 2)	1
   (1, 1)	1
   (2, 0)	1

其中，`(行索引, 列索引)` 表示非零元素的位置，而 `1` 表示该位置的非零元素值。

### 2.1.2 RNA 测序数据分析

RNA 测序 (RNA-Seq) 是一种更先进的基因表达分析技术，它可以提供比微阵列更高的分辨率和准确性。RNA-Seq 数据也通常以稀疏矩阵的形式存储，其中行表示转录本，列表示样品，非零元素表示转录本在该样品中的表达水平。

**代码块 2：RNA-Seq 数据稀疏矩阵**

import pandas as pd
import scipy.sparse

# 加载 RNA-Seq 数据
data = pd.read_csv('rna_seq_data.csv', index_col=0)

# 创建稀疏矩阵
sparse_matrix = scipy.sparse.csr_matrix(data.values)

# 打印稀疏矩阵
print(sparse_matrix)

**逻辑分析：**

* `pd.read_csv` 函数用于从 CSV 文件中加载 RNA-Seq 数据。
* `scipy.sparse.csr_matrix` 函数用于创建 CSR 格式的稀疏矩阵。
* 打印稀疏矩阵时，它将以与微阵列数据稀疏矩阵类似的格式显示。

## 2.2 蛋白质组学分析

### 2.2.1 蛋白质-蛋白质相互作用网络

蛋白质-蛋白质相互作用网络 (PPI) 是蛋白质相互作用的图表示，其中节点表示蛋白质，边表示蛋白质之间的相互作用。PPI 网络通常以稀疏矩阵的形式存储，其中行和列表示蛋白质，非零元素表示蛋白质之间的相互作用。

**代码块 3：PPI 网络稀疏矩阵**

import networkx as nx
import scipy.sparse

# 创建一个 PPI 网络图
G = nx.Graph()
G.add_edges_from([(1, 2), (1, 3), (2, 4), (3, 4)])

# 创建稀疏矩阵
sparse_matrix = scipy.sparse.csr_matrix(nx.adjacency_matrix(G))

# 打印稀疏矩阵
print(sparse_matrix)

**逻辑分析：**

* `networkx` 库用于创建 PPI 网络图。
* `nx.adjacency_matrix` 函数用于将网络图转换为稀疏矩阵。
* 打印稀疏矩阵时，它将以与微阵列数据稀疏矩阵类似的格式显示。

### 2.2.2 蛋白质功能注释

蛋白质功能注释是指将蛋白质与它们的功能联系起来的过程。蛋白质功能注释信息通常以稀疏矩阵的形式存储，其中行表示蛋白质，列表示功能术语，非零元素表示蛋白质与该功能术语的关联程度。

**代码块 4