时间序列分解与MATLAB应用：深入解读与技巧提升

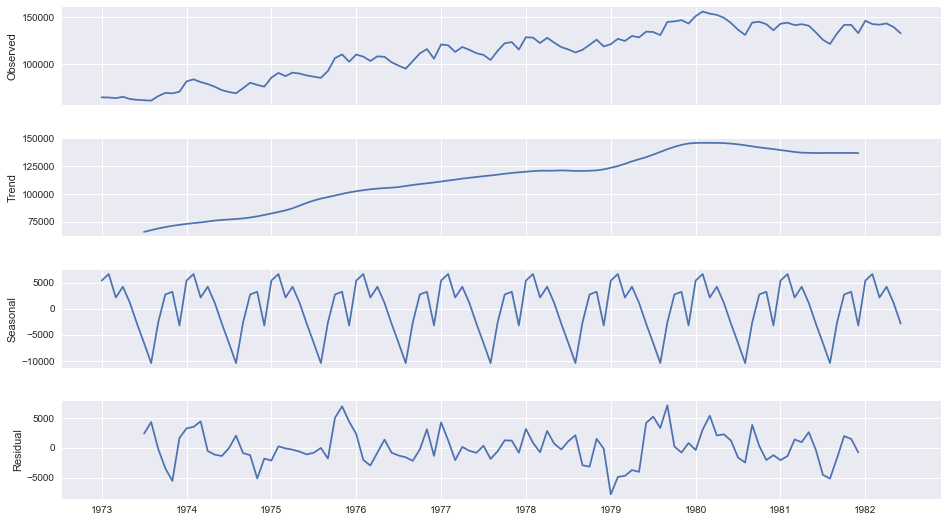
# 1. 时间序列分解基础

在时间序列分析中，分解是将复杂的时间序列数据分解为趋势、季节性和随机成分的方法，这种方法在各种应用中都非常有用，尤其是用于预测和理解数据背后的模式。本章将深入探讨时间序列分解的基础，包括其理论基础和分解方法的原理。

时间序列数据通常包含长期趋势、季节性周期和不规则波动。理解这些组成部分是如何相互作用的，对于数据科学家和分析师来说至关重要。通过分解，我们可以分别研究每个组成部分，以更好地理解它们对整体时间序列行为的影响。本章将从基础概念讲起，为后续章节中使用MATLAB进行时间序列分解的高级应用和优化技术打下坚实的基础。

我们将从时间序列分解的最简单的概念开始，逐步深入到各个组成部分，为读者提供一个清晰的框架，以便后续章节可以在此基础上进一步探索和应用。下面章节将开始详细介绍时间序列分解的理论基础，逐步展开，带领读者深入理解时间序列的结构和分解技术。

# 2. MATLAB在时间序列分析中的应用

## 2.1 MATLAB的基础操作与时间序列对象

### 2.1.1 MATLAB界面及基本命令

MATLAB（Matrix Laboratory的缩写）是一种用于算法开发、数据可视化、数据分析以及数值计算的高级编程语言和交互式环境。MATLAB的界面主要由几个核心部分组成，包括命令窗口（Command Window）、编辑器（Editor）、工作空间（Workspace）、路径和路径管理器（Path and Path Manager）、以及图形用户界面（GUI）组件。

在命令窗口中，用户可以输入命令行操作，直接对数据进行处理和分析。例如，创建一个矩阵并进行基本操作：

A = [1 2 3; 4 5 6; 7 8 9]; % 创建一个3x3矩阵
B = A + 10;                 % 将矩阵A的每个元素增加10
disp(B);                    % 显示矩阵B的内容

在上述代码块中，首先通过方括号定义了一个3x3的矩阵A，并用分号隔开行。接着执行矩阵的标量加法，将矩阵A的每个元素增加10，结果存储在矩阵B中。最后，使用`disp`函数将矩阵B的内容显示在命令窗口中。

### 2.1.2 时间序列数据对象的创建与操作

在MATLAB中处理时间序列数据，一个关键步骤是将原始数据转换为时间序列对象。MATLAB通过`timeseries`函数支持时间序列对象的创建，这使得数据分析和操作更为方便。例如，创建一个时间序列对象并分析其特性：

data = [*.***.***.***.6 6.7 7.8]; % 假设这是一个季度数据
time = datetime({'2020-01-01'; '2020-04-01'; '2020-07-01'; '2020-10-01'; '2021-01-01'; '2021-04-01'}, 'InputFormat', 'yyyy-MM-dd');
ts = timeseries(data, time);       % 创建时间序列对象

上述代码中，`data`数组包含了时间序列的观测值，`time`是一个datetime数组，定义了这些观测值对应的时间点。`timeseries`函数将这两个数组合并为一个时间序列对象。MATLAB提供了一系列操作时间序列对象的方法，例如计算移动平均、季节性调整等。

## 2.2 时间序列分解方法

### 2.2.1 加法模型与乘法模型的区别

在时间序列分析中，两种常见的分解模型是加法模型和乘法模型。它们用于将时间序列数据分解为趋势（Trend）、季节性（Seasonality）和随机成分（Irregular）。

加法模型假设时间序列的各个组成部分是相加的关系，即：

\[ Y_t = T_t + S_t + I_t \]

其中，\( Y_t \) 是在时间点 \( t \) 的观测值，\( T_t \) 是趋势成分，\( S_t \) 是季节性成分，\( I_t \) 是随机成分。

乘法模型则假设这些成分是相乘的关系：

\[ Y_t = T_t \times S_t \times I_t \]

在实际应用中，选择加法模型还是乘法模型取决于各个成分之间是否表现出相对独立的变化。乘法模型通常适用于数据随时间增长而波动幅度也增大的情况。

### 2.2.2 季节性分解技术

季节性分解是时间序列分析中的一个重要步骤。MATLAB提供了多种季节性分解技术，包括经典的季节性分解方法和现代基于统计的方法。

经典的方法之一是X-11，这是一种广泛使用的季节性调整程序。而在MATLAB中，用户可以利用`decompose`函数进行季节性分解：

% 假设我们有一个季节性数据集
data = [***]; % 每个月的销售额
time = datetime({'2020-01'; '2020-02'; '2020-03'; '2020-04'; '2020-05'; '2020-06'; ...
                 '2020-07'; '2020-08'; '2020-09'; '2020-10'; '2020-11'; '2020-12'}, ...
                 'Format', 'yyyy-MM');
ts = timeseries(data, time);
[detrended, seasonal, irregular, trend] = decompose(ts);

在执行上述代码后，`decompose`函数将返回四个时间序列对象：去趋势后的数据、季节性成分、随机成分和趋势成分。这些成分可以用来深入分析数据的动态特性。

## 2.3 MATLAB中的时间序列分解实践

### 2.3.1 使用内置函数进行分解

MATLAB的内置函数使得时间序列分解变得更加便捷。使用`detrend`函数可以去除数据的趋势成分，而`seasonaldecompose`函数则可以更进一步地分解季节性成分和随机成分。

% 继续使用前面创建的时间序列对象ts
detrendedData = detrend(ts); % 去除趋势成分
[seasonalData, trendData, residual] = seasonaldecompose(ts); % 季节性分解

% 可视化去趋势和分解结果
figure;
subplot(3,1,1);
plot(detrendedData);
title('Detrended Time Series Data');
subplot(3,1,2);
plot(seasonalData);
title('Seasonal Component');
subplot(3,1,3);
plot(residual);
title('Irregular Component');

上述代码块首先对时间序列对象`ts`进行去趋势处理，然后使用`seasonaldecompose`函数进行季节性分解，得到季节成分、趋势成分和随机成分。最后，使用`subplot`函数将不同的成分绘制在同一图形的不同部分，便于比较和分析。

### 2.3.2 分解结果的解读与分析

分解结果提供了时间序列数据的深层次理解。通过对趋势成分的分析，我们可以识别长期的业务趋势；通过对季节成分的分析，我们可以了解季节性因素对业务的影响；通过对随机成分的分析，我们可以识别并处理异常值。

例如，分解出的季节性成分可以使用箱线图来可视化，帮助我们更好地了解每个季节的波动情况：

boxplot(seasonalData.Data, 'Labels', {'Q1', 'Q2', 'Q3', 'Q4'});
title('Seasonal Boxplot');

在上述代码块中，`boxplot`函数被用来创建季节性成分的箱线图。`SeasonalData.Data`包含了季节性成分的值，而`Labels`参数定义了箱线图的x轴标签，对应不同的季度。结果能够展示出每个季度数据的分布情况，帮助我们理解季节变化对时间序列数据的影响。

为了深入理解分解结果，可以进一步对趋势和季节性成分进行统计分析，比如计算相关系数、拟合线