MATLAB长短期记忆网络（LSTM）实战：时间序列预测高级篇

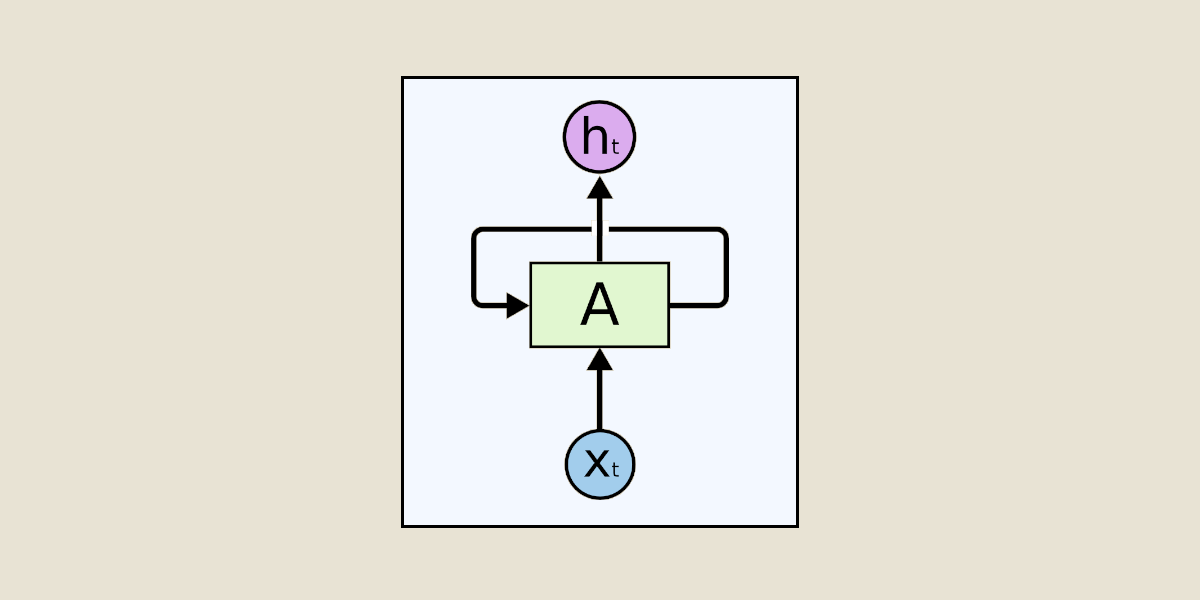
# 1. 长短期记忆网络（LSTM）概述

长短期记忆网络（LSTM）作为深度学习领域的一种特殊类型的循环神经网络（RNN），它在处理和预测时间序列数据方面表现出了独特的优越性。在这一章节，我们将对LSTM进行一个基础概述，包括它的基本概念、结构特点和为何它特别适用于解决长期依赖问题。

## LSTM网络的理论基础

### LSTM网络的工作原理

LSTM通过引入门控机制来解决传统RNN的梯度消失和梯度爆炸问题。在LSTM中，隐藏状态是由三个主要的门控结构控制：遗忘门、输入门和输出门。这些门控制着信息的流入和流出，确保只有相关的信息会被保留或遗忘。

### LSTM单元结构和优势

每个LSTM单元包含一个记忆单元，它能够存储序列信息并允许网络学习何时添加或移除信息。LSTM的优势在于能够保持长期记忆，同时根据序列中不同时刻的数据来更新或遗忘信息，这使它在处理时间序列数据时比传统的RNN更加有效。

LSTM网络的核心优势在于它能够通过精妙的门控制机制来维护和操作一个长期的状态，这对于模型捕捉和利用时间序列数据中的长期依赖关系至关重要。在接下来的章节中，我们将深入探讨如何在MATLAB中利用LSTM进行网络构建和优化，以及如何将这些理论知识应用于实际的数据分析和预测问题。

# 2. MATLAB LSTM网络构建基础

### 2.1 LSTM网络的理论基础

#### 2.1.1 LSTM网络的工作原理

长短期记忆网络（LSTM）是一种特殊类型的循环神经网络（RNN），它能够学习长期依赖信息。LSTM的关键是其能够通过精心设计的门机制来解决传统RNN的长期依赖问题。LSTM单元主要包含三个门：遗忘门（forget gate）、输入门（input gate）和输出门（output gate）。

- **遗忘门**：决定哪些信息需要从单元状态中删除，即决定丢弃什么信息。
- **输入门**：决定哪些新信息将要存储在单元状态中，以及如何更新这个状态。
- **输出门**：决定下一个隐藏状态的输出值。

遗忘门和输入门共同工作，确保信息在需要时可以被添加和删除。在任何时间点，LSTM都可以选择性地记住或忽略信息，这使得它在处理序列数据时更加有效。

LSTM的工作原理可以通过以下伪代码表达：

for each input in sequence:
    forget gate: f_t = σ(W_f * [h_(t-1), x_t] + b_f)
    input gate: i_t = σ(W_i * [h_(t-1), x_t] + b_i)
    candidate state: 	ñ_t = tanh(W_c * [h_(t-1), x_t] + b_c)
    state: c_t = f_t * c_(t-1) + i_t * ñ_t
    output gate: o_t = σ(W_o * [h_(t-1), x_t] + b_o)
    hidden state: h_t = o_t * tanh(c_t)

其中，σ 表示sigmoid函数，tanh表示双曲正切函数，W_和b_分别是权重矩阵和偏置向量。

#### 2.1.2 LSTM单元结构和优势

LSTM单元结构由细胞状态（cell state）、隐藏状态（hidden state）以及上述的三个门组成。细胞状态可以认为是一个信息高速公路，信息可以沿着这个高速公路流动，而三个门可以控制信息的流动：遗忘门控制遗忘信息，输入门控制添加信息，输出门控制输出信息。

LSTM之所以在序列数据处理中具有优势，原因在于其内部结构允许网络在必要时通过门机制保持信息不被遗忘。这样的结构可以有效地避免长期依赖问题，因为即使时间间隔很长，信息也可以被保留并用于决策过程。此外，LSTM能够通过组合门的操作来进行复杂的逻辑操作，这使得它非常适合处理需要长期依赖的复杂任务，如语言模型、时间序列预测等。

### 2.2 MATLAB中的LSTM网络组件

#### 2.2.1 LSTM层的配置和初始化

在MATLAB中构建LSTM网络，首先需要配置网络层，然后初始化模型权重。MATLAB通过深度学习工具箱提供了一系列构建和训练LSTM网络的函数和类。

layers = [ ...
    sequenceInputLayer(1, 'Name', 'input') % 输入层，假设每个时间步的输入大小为1
    lstmLayer(50, 'OutputMode', 'sequence', 'Name', 'lstm') % LSTM层，50个单元
    fullyConnectedLayer(1) % 全连接层，用于输出预测结果
    regressionLayer]; % 回归层，用于处理时间序列预测任务

在上述代码中，`lstmLayer`函数被用来创建一个LSTM层，其中包含50个单元，并设置输出模式为'sequence'，表示每个时间步都会输出一个结果。

#### 2.2.2 LSTM网络的训练和验证

在配置好LSTM网络的层之后，下一步是训练网络。在MATLAB中，使用`trainNetwork`函数可以实现网络的训练：

options = trainingOptions('adam', ...
    'MaxEpochs',100, ...
    'GradientThreshold',1, ...
    'InitialLearnRate',0.005, ...
    'LearnRateSchedule','piecewise', ...
    'LearnRateDropPeriod',125, ...
    'LearnRateDropFactor',0.2, ...
    'Verbose',0, ...
    'Plots','training-progress');

net = trainNetwork(trainingData, layers, options);

在此处，`trainingOptions`函数用于配置训练选项，例如选择优化器（'adam'），设置最大训练周期（'MaxEpochs'），梯度阈值（'GradientThreshold'），初始学习率（'InitialLearnRate'）等。然后通过`trainNetwork`函数使用训练数据和配置的层来训练网络，并返回训练好的网络对象。

#### 2.2.3 权重和偏置的调整方法

在训练过程中，权重和偏置会根据网络的训练进度自动调整。然而，在特定情况下，可能需要人工调整权重和偏置以优化模型性能。在MATLAB中，可以通过以下代码手动更新权重和偏置：

% 访问LSTM层的权重和偏置
lstmWeights = net.Layers(2).Weights;
lstmBias = net.Layers(2).Bias;

% 更新权重和偏置
lstmWeights = lstmWeights + 0.01; % 增加1%权重
lstmBias = lstmBias + 0.05; % 增加5%偏置

% 将更新后的权重和偏置重新分配到网络中
net.Layers(2).Weights = lstmWeights;
net.Layers(2).Bias = lstmBias;

% 验证网络性能是否提高
YPred = predict(net, testData);

通过上述代码段，我们可以获取特定层（此处为第二层，即LSTM层）的权重和偏置，然后对其进行必要的调整，并将调整后的参数赋值回原网络中，最后重新进行预测并验证模型性能。

### 2.3 时间序列预测的预备步骤

#### 2.3.1 数据预处理和归一化

在进行时间序列预测前，数据预处理是一个至关重要的步骤。这包括数据清洗、标准化或归一化、缺失值处理等。对于时间序列数据，归一化操作可以提高模型训练的效率和稳定性。

在MATLAB中，可以使用以下步骤进行数据归一化：

% 假设原始数据存储在变量data中
% 计算均值和标准差
mu = mean(data);
sig = std(data);

% 应用归一化公式
normalizedData = (data - mu) / sig;

% 为了验证归一化的效果，可以绘制直方图
figure;
histogram(data, 'Normalization', 'pdf');
title('原始数据直方图');
figure;
histogram(normalizedData, 'Normalization', 'pdf');
title('归一化数据直方图');

上述代码展示了如何计算数据的均值和标准差，并应用线性归一化公式对数据进行归一化处理。通过比较归一化前后的直方图，可以直观地看到数据分布的变化。

#### 2.3.2 划分训练集和测试集

为了评估模型的泛化能力，在数据预处理后，需要将数据划分为训练集和测试集。在MATLAB中，这可以通过以下代码实现：

% 假设归一化后的数据存储在变量normalizedData中
numTimeStepsTrain = floor(0.9*numel(normalizedData));
dataTrain = normalizedData(1:numTimeStepsTrain+1);
dataTest = normalizedData(numTimeStepsTrain+1:end);

% 绘制训练集和测试集
figure;
plot(dataTrain);
hold on;
plot(numTimeStepsTrain+1:numel(dataTrain), dataTest, 'r');
hold off;
title('训练集和测试集');
legend('训练数据', '测试数据');

通过上述代码，我们将数据集的90%作为训练集，剩余的10%作为测试集。然后，绘制训练集和测试集的图形，以便可视化地验证数据集划分的效果。

#### 2.3.3 序列填充和批处理策略

在处理时间序列数据时，数据不完整的情况可能会导致序列长度不一，因此需要序列填充来使所有输入序列长度统一。此外，合理的批处理策略可以帮助提升模型训练的效率和稳定性。

在MATLAB中，可以使用`padSequence`函数来填充序列：

% 假设输入数据存储在cell数组X中
Y = padSequence(X);

% 划分批次进行训练
numTimeStepsTrain = floor(0.9*numel(Y));
XTrain = Y(1:numTimeStepsTrain+1);
XTest = Y(numTimeStepsTrain+1:end);

通过上述代码，我们首先使用`padSequence`函数对输入数据`X`进行填充，然后将填充后的数据`Y`划分为训练集和测试集。通过这种方式，可以确保所有序列长度一致，从而便于模型进行批处理训练。

以上内容涵盖了LSTM网络构建的基础知识点，从理论基础到实际应用细节，让读者能够理解并掌握在MATLAB环境下构建LSTM网络的核心步骤和关键策略。

# 3. MATLAB LSTM实战案例分析

## 3.1 金融时间序列预测

### 3.1.1 股票价格预测模型构建

在这一小节中，我们将介绍如何使用MATLAB来构建一个LSTM模型，这个模型将用于预测股票价格。首先需要了解股票价格的时间序列数据特点，这是典型的非线性、高波动性和动态相关性数据集。为了构建模型，我们会涉及以下步骤：

1. **数据准备**：获取股票历史价格数据，这些数据可以从金融市场分析工具或者金融服务提供商处得到，然后将数据导入MATLAB环境。

2. **数据预处理**：清洗数据，处理缺失值，然后对数据进行归一化处理，使其分布在一个较小的范围内，通常为[0,1]。这是为了提高模型训练的稳定性和效果。

3. **序列构建**：从时间序列数据中提取特征，创建输入序列和目标序列，对于股票价格预测，目标序列一般是未来价格，输入序列可以是过去一段时间的价格。

4. **模型创建与训练**：使用MATLAB深度学习工具箱创建一个LSTM网络，网络结构包括输入层、LSTM层、全连接层和输出层。然后使用准备好的数据对模型进行训练，期间利用训练集进行模型参数的调整，并使用验证集对模型性能进行监控。

下面是相应的MATLAB代码段，其中`stockPrices`是一