透视变换与几何约束：揭秘OpenCV双目相机标定原理，深入理解标定本质

# 1. OpenCV双目相机标定概述

OpenCV双目相机标定是一种通过已知几何结构的标定板，来估计双目相机内参和外参的技术。通过标定，可以消除相机畸变，提高双目立体视觉系统的精度和鲁棒性。

双目相机标定涉及以下关键步骤：

1. **标定板检测与特征点提取：**检测标定板并提取特征点，如角点或圆圈。
2. **相机参数估计：**根据特征点匹配和几何约束，估计相机的内参（焦距、畸变系数）和外参（平移、旋转）。
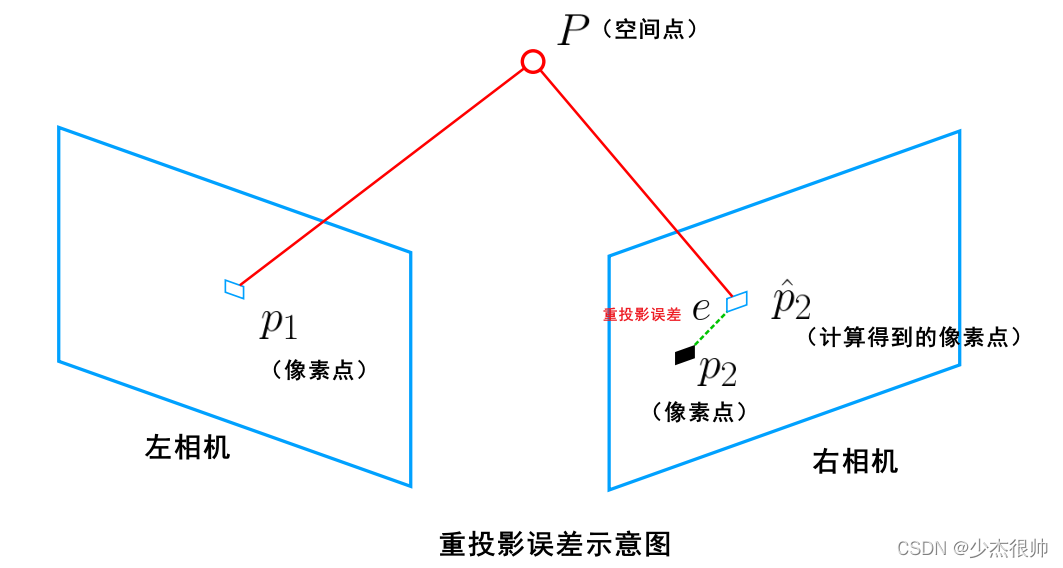
3. **标定结果评估：**通过重投影误差等指标，评估标定结果的精度和可靠性。

# 2. 透视变换理论基础

### 2.1 透视投影模型

透视投影模型是一种将三维场景投影到二维平面的数学模型。它假设光线从三维场景中的点发出，通过一个称为投影中心的点，并与一个称为投影平面的平面相交。投影平面上与光线相交的点就是三维场景中点的二维投影。

透视投影模型可以用一个矩阵方程来表示：

[x, y, z, 1] * [M] = [x', y', z', 1]

其中：

* `[x, y, z, 1]` 是三维场景中点的齐次坐标。
* `[M]` 是投影矩阵。
* `[x', y', z', 1]` 是二维投影平面上点的齐次坐标。

投影矩阵 `[M]` 由以下内容组成：

* 相机的内参矩阵：包含相机的焦距、光学中心和畸变参数。
* 相机的外参矩阵：包含相机的旋转和平移。

### 2.2 齐次坐标系

齐次坐标系是一种扩展的坐标系，它在笛卡尔坐标系中添加了一个额外的维度。齐次坐标系中的点表示为 `[x, y, z, w]`，其中 `w` 是一个非零标量。齐次坐标系允许使用矩阵乘法来表示透视变换，这使得计算更加方便。

齐次坐标系中的点可以表示为笛卡尔坐标系中的点，方法是将齐次坐标系中的 `w` 分量除以其他三个分量。例如，齐次坐标系中的点 `[x, y, z, w]` 可以表示为笛卡尔坐标系中的点 `[x/w, y/w, z/w]`。

### 2.3 相机模型

相机模型是透视投影模型的具体实例。相机模型定义了相机的内参和外参。

相机的内参包括：

* 焦距：相机的焦距是光学中心到投影平面的距离。
* 光学中心：光学中心是投影平面上光轴与投影平面的交点。
* 畸变参数：畸变参数描述了相机的透镜畸变。

相机的外参包括：

* 旋转矩阵：旋转矩阵描述了相机相对于世界坐标系的旋转。
* 平移向量：平移向量描述了相机相对于世界坐标系的平移。

相机模型可以用来将三维场景中的点投影到二维图像平面上。

# 3. 几何约束分析

### 3.1 相机标定板几何约束

相机标定板通常采用棋盘格图案，其几何约束主要体现在棋盘格的网格结构和已知棋盘格尺寸上。

#### 棋盘格网格结构

棋盘格网格结构由交错排列的黑色和白色方格组成，每个方格大小已知。这种网格结构提供了丰富的特征点