解密欧拉函数与最小公倍数的秘密

# 1.1 欧拉函数的定义与性质

欧拉函数，也称为欧拉φ函数，是一个重要的数论函数，用符号φ(n)表示。它表示小于等于n且与n互质的正整数的个数。欧拉函数的计算方法有多种，可以通过素数分解或者辗转相除法进行求解。欧拉函数具有一些特殊的性质，比如对于任意两个互质的正整数a和b，φ(ab) = φ(a) * φ(b)。这个性质在实际应用中有着重要的意义，特别是在密码学领域中。欧拉函数的特殊性质还涉及到欧拉定理等数论重要定理，对于解决一些数论问题非常有帮助。深入理解欧拉函数的定义和性质，有助于更好地应用它解决实际问题。

# 2. 欧拉函数的计算与算法

- **2.1 欧拉函数的计算方法**
- 1.1.1 欧拉函数的基本概念
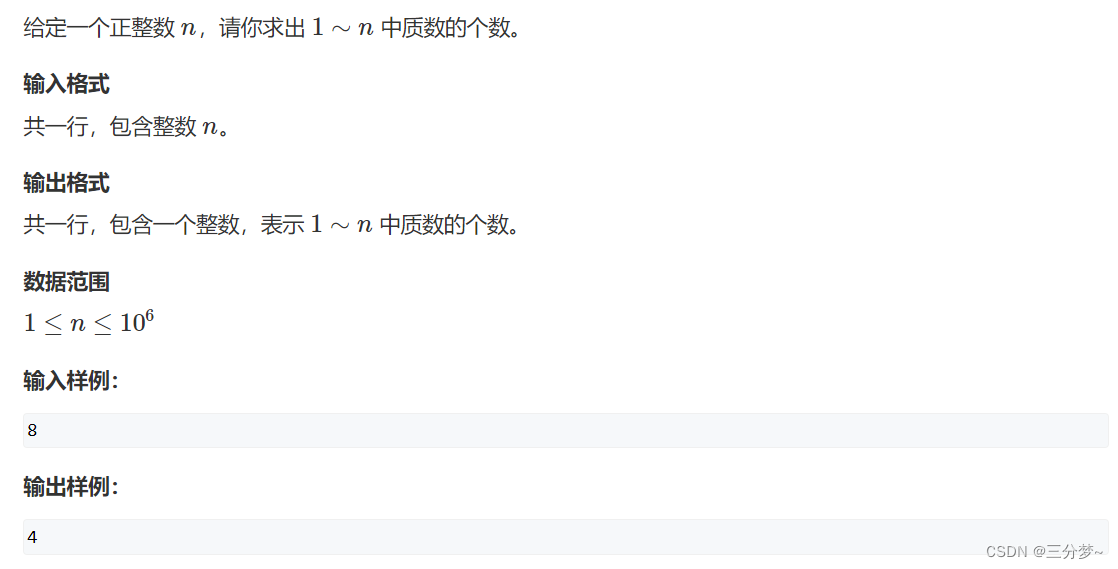
欧拉函数（Euler's Totient Function）用符号φ(n)表示，表示小于等于n且与n互质的正整数的个数。例如，φ(8)=4，因为1, 3, 5, 7均与8互质。
- 1.1.2 欧拉函数的计算方法
1. **辗转相除法求欧拉函数**
辗转相除法，又称欧几里得算法，是一种计算最大公约数的算法，可用于计算欧拉函数。例如，对于n=10，求φ(10)：

       def gcd(a, b):
           if b == 0:
               return a
           return gcd(b, a % b)
       def euler_totient_function(n):
           count = 0
           for i in range(1, n+1):
               if gcd(i, n) == 1:
                   count += 1
           return count
       print(euler_totient_function(10))  # Output: 4

2. **素数分解求欧拉函数**
利用n的质因数分解形式，可通过公式计算出欧拉函数的值。如，n=p*q，则φ(n) = (p-1)(q-1)。
3. **多组数欧拉函数的计算**
如果需要计算多个数的欧拉函数，建议使用欧拉筛算法，能够高效计算一系列数的欧拉函数值。
- 1.1.3 欧拉函数的特殊性质
- 若n为质数p，则φ(n) = n-1。
- 若n为两个质数p、q的乘积，则φ(p*q) = (p-1)(q-1)。
- 若n能够被p整除，且p为质数，则φ(n) = φ(n/p) * p。

- **2.2 欧拉函数的应用**
- 2.2.1 RSA加密算法中的欧拉函数应用
欧拉函数在RSA公钥加密算法中扮演重要角色。RSA算法基于两个大素数p、q的乘积n，选取与φ(n)=(p-1)(q-1)互质的e作为公钥的一部分。
- 2.2.2 欧拉函数在数论中的重要性
欧拉函数在数论中具有重要意义，通过欧拉函数可以推导出费马小定理等数论定理，用于解决模幂运算等问题。
- 2.2.3 欧拉函数在密码学中的应用
除了RSA算法，欧拉函数还在密码学的各个领域广泛应用，包括数字签名、身份认证、安全通信等方面。在数据安全性方面发挥着不可或缺的作用。

# 3. 最小公倍数的计算与应用

- **3.1 最小公倍数的计算方法**

在数学中，最小公倍数是指几个数共有的倍数中最小的一个。计算最小公倍数的方法有多种，其中比较基础的方法是通过列举两个数的倍数，找到它们共有的最小倍数，这种方法适用于小数据量的情况。

- **3.1.1 基本方法求最小公倍数**

以计算7和10的最小公倍数为例，首先列举它们的倍数：

7的倍数：7, 14, 21, 28, 35, 42, 49, 56, 63, 70, ...
10的倍数：10, 20, 30, 40, 50, 60, 70, ...

可以看到，它们共有的最小倍数是70。

- **3.1.2 欧拉函数优化求最小公倍数**

除了基本方法外，欧拉函数也可用来优化求最小公倍数的过程。通过欧拉函数的性质，可以使用以下公式计算两个数 a 和