利用MATLAB正态分布函数进行数据拟合：揭示数据的潜在规律，洞悉数据本质

# 1. MATLAB正态分布函数概述

正态分布函数，又称高斯分布函数，是一种连续概率分布，在自然界和科学研究中广泛存在。它描述了随机变量在均值周围分布的概率密度。MATLAB中提供了强大的正态分布函数实现，可以方便地用于数据分析、建模和统计推断。

本章将概述MATLAB正态分布函数的基本概念和功能，包括其定义、性质、MATLAB中的语法和用法。通过理解这些基础知识，我们可以为进一步深入探索正态分布函数及其在数据分析中的应用奠定基础。

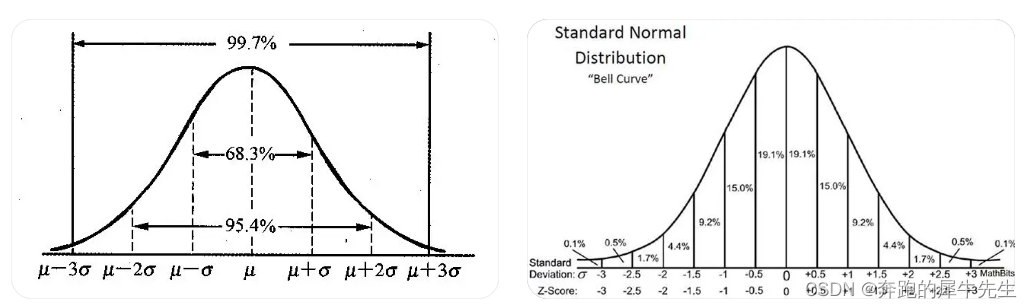
# 2. 正态分布函数的理论基础

### 2.1 正态分布的定义和性质

正态分布，又称高斯分布，是一种连续概率分布，其概率密度函数呈钟形曲线。正态分布具有以下性质：

- **对称性：**概率密度函数关于其均值对称。
- **单峰性：**概率密度函数只有一个峰值，位于均值处。
- **渐近性：**概率密度函数的尾部呈指数衰减，这意味着极端值出现的概率很小。
- **正态性：**如果一个随机变量的分布服从正态分布，那么它的线性组合也服从正态分布。

### 2.2 正态分布函数的数学表达式

正态分布函数的概率密度函数为：

f(x) = (1 / (σ√(2π))) * e^(-(x - μ)² / (2σ²))

其中：

- x：随机变量
- μ：均值
- σ：标准差

正态分布函数的累积分布函数为：

F(x) = ∫_{-∞}^{x} (1 / (σ√(2π))) * e^(-(x - μ)² / (2σ²)) dx

累积分布函数表示在给定 x 值下，随机变量小于或等于 x 的概率。

# 3. 正态分布函数在数据拟合中的应用

### 3.1 数据拟合的概念和步骤

数据拟合是指根据给定的一组数据点，找到一条曲线或函数，使其与数据点尽可能接近，从而揭示数据中的规律和趋势。数据拟合在科学研究、工程设计和数据分析等领域有着广泛的应用。

数据拟合的过程通常包括以下步骤：

1. **数据收集：**收集与研究问题相关的原始数据。
2. **数据预处理：**对原始数据进行清理和处理，包括去除异常值、处理缺失值和转换数据格式。
3. **模型选择：**根据数据的特点和研究目的，选择合适的拟合模型，例如线性回归、多项式回归或正态分布函数。
4. **模型参数估计：**使用最小二乘法或其他优化算法，估计模型的参数，使其与数据点最匹配。
5. **模型评估：**通过计算残差平方和、决定系数等指标，评估拟合模型的准确性和适用性。
6. **模型应用：**利用拟合模型对新数据进行预测或分析。

### 3.2 正态分布函数在数据拟合中的优势

正态分布函数是一种常用的数据拟合模型，具有以下优势：

- **广泛的适用性：**正态分布是一种常见的概率分布，适用于