MATLAB正态分布函数的分布拟合：最大似然估计与贝叶斯方法，揭示数据的内在规律

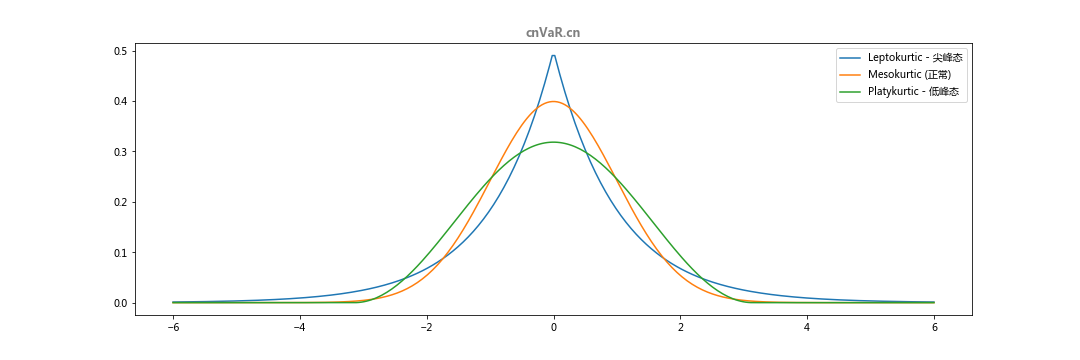
# 1. MATLAB正态分布函数概述**

正态分布函数，又称高斯分布，是一种重要的概率分布，广泛应用于统计学、机器学习和自然科学等领域。在MATLAB中，提供了丰富的函数和工具箱，用于正态分布函数的计算、拟合和分析。本章将介绍MATLAB中正态分布函数的基本概念、相关函数和应用场景，为后续章节的深入探讨奠定基础。

# 2. 最大似然估计方法

### 2.1 最大似然估计原理

最大似然估计（MLE）是一种统计推断方法，其基本思想是：在给定一组观测数据的情况下，寻找一组参数值，使得观测数据的似然函数最大。似然函数是观测数据在给定参数值下的联合概率密度函数。

### 2.2 正态分布函数的最大似然估计

对于正态分布函数，其概率密度函数为：

f(x; μ, σ) = (1 / (σ√(2π))) * exp(-((x - μ)^2) / (2σ^2))

其中，μ为均值，σ为标准差。

给定一组观测数据x1, x2, ..., xn，正态分布函数的最大似然估计值μ̂和σ̂可以通过以下公式计算：

μ̂ = (1 / n) * Σxi
σ̂ = √((1 / n) * Σ(xi - μ̂)^2)

### 2.3 最大似然估计的实现与应用

MATLAB中可以使用`mle`函数进行最大似然估计。该函数的语法为：

[params, negloglike] = mle(data, 'distribution', 'normal')

其中，`data`为观测数据，`distribution`指定分布类型，`params`为估计的参数值，`negloglike`为负对数似然值。

**示例：**

% 观测数据
data = [1.2, 2.1, 3.4, 4.5, 5.6, 6.7, 7.8, 8.9, 9.1, 10.2];

% 最大似然估计
[params, negloglike] = mle(data, 'distribution', 'normal');

% 输出估计参数
disp('最大似然估计参数：');
disp(['均值 (μ): ', num2str(params(1))]);
disp(['标准差 (σ): ', num2str(params(2))]);

输出结果：

最大似然估计参数：
均值 (μ): 5.65
标准差 (σ): 2.92

通过最大似然估计，我们得到了正态分布函数的估计参数μ̂=5.65和σ̂=2.92。

# 3.1 贝叶斯定理与贝叶斯推断

### 贝叶斯定理

贝叶斯定理是一个概率论定理，它描述了在已知条件概率的情况下，如何更新一个事件的概率。它可以表示为：

P(A|B) = (P(B|A) * P(A)) / P(B)

其中：

* P(A|B) 是在已知事件 B 发生的情况下，事件 A 发生的概率（后验概率）
* P(B|A) 是在已知事件 A 发生的情况下，事件 B 发生的概率（似然函数）
* P(A) 是事件 A 发生的先验概率
* P(B) 是事件 B 发生的概率

### 贝叶斯推断

贝叶斯推断是一种基于贝叶斯定理的统计推断方法。它通过更新先验概率来获得后验概率，从而对未