MATLAB正态分布参数估计：揭示数据背后的分布规律

# 1. MATLAB中正态分布简介**

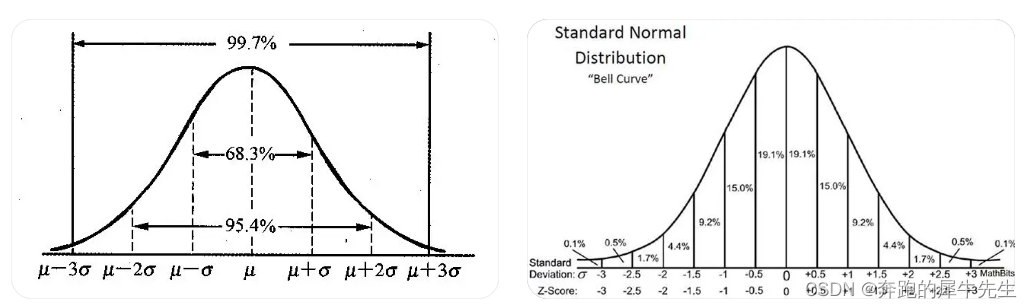
正态分布，又称高斯分布，是一种连续概率分布，在统计学和概率论中广泛应用。它以其钟形曲线而闻名，其特征在于均值和标准差两个参数。

在MATLAB中，正态分布可以用`normrnd`函数生成。该函数接受两个参数：均值和标准差。例如，以下代码生成一个均值为0、标准差为1的正态分布样本：

x = normrnd(0, 1, 1000);

# 2. 正态分布参数估计的理论基础

正态分布，又称高斯分布，是一种连续概率分布，在自然界和工程应用中广泛存在。正态分布参数估计是统计学中的一项基本任务，其目的是从样本数据中推断出正态分布的未知参数。本章节将介绍正态分布参数估计的理论基础，包括正态分布的概率密度函数和最大似然估计法。

### 2.1 正态分布的概率密度函数

正态分布的概率密度函数为：

f(x) = (1 / (σ√(2π))) * exp(-(1 / 2) * ((x - μ) / σ)^2)

其中：

* x 为随机变量
* μ 为正态分布的均值
* σ 为正态分布的标准差

概率密度函数表示在给定均值和标准差的情况下，随机变量取特定值的概率。正态分布的概率密度函数呈钟形曲线，其中心为均值，两侧对称。

### 2.2 最大似然估计法

最大似然估计法是一种参数估计方法，其基本思想是：在所有可能的参数值中，选择使样本数据似然函数最大的参数值作为估计值。

对于正态分布，似然函数为：

L(μ, σ) = (1 / (n * (2πσ^2)^(n/2))) * exp(-(1 / 2) * Σ((x_i - μ) / σ)^2)

其中：

* n 为样本容量
* x_i 为样本数据

最大似然估计法通过求解似然函数对参数 μ 和 σ 的偏导数并令其为 0 来获得参数估计值：

μ_hat = (1 / n) * Σx_i
σ_hat^2 = (1 / n) * Σ((x_i - μ_hat)^2)

最大似然估计法是一种常用的参数估计方法，其优点在于：

* 具有渐近无偏性：当样本容量足够大时，最大似然估计量是无偏的。
* 具有渐近有效性：当样本容量足够大时，最大似然估计量是有效率的，即具有最小的方差。

# 3.1 数据的读取和预处理

在进行正态分布参数估计之前，需要先读取和预处理数据。MATLAB提供了多种读取数据的方法，例如：

% 从文本文件读取数据
data = load('data.txt');

% 从 CSV 文件读取数据
data = csvread('data.csv');

% 从 Excel 文件读取数据
data = xlsread('data.xlsx');

读取数据后，需要对数据进行预处理，以确保数据符合正态分布的假设。预处理步骤包括：

- **缺失值处理：**缺失值会影响参数估计的准确性。可以删除缺失值，也可以使用插值或平均值填充缺失值。
- **异常值处理：**异常值会扭曲参数估计。可以删除异常值，也可以使用 Winsorization 或 Tukey 法对异常值进行处理。
- **数据转换：**如果数据不符合正态分布，可以进行数据转换，例如对数转换或平方根转换，以使数据更接近正态分布。

### 3.2 参数估计方法

MATLAB提供了多种正态分布参数估计方法，包括：

#### 3.2.1 最大似然估计法

最大似然估计法（MLE）是一种经典的参数估计方法。MLE通过最大化似然函数来估计参数。正态分布的似然函数为：

L(μ, σ) = (2πσ^2)^(-n/2) * exp(-Σ(x_i - μ)^2 / (2σ^2))

其中，μ和σ分别为正态分布的均值和标准差，x_i为数据样本。

MATLAB中使用 `mle` 函数进行最大似然估计：

% 估计正态分布的参数
params = mle(data, 'distribution', 'normal');

% 获取估计的均值和标准差
mu = params(1);
sigma = params(2);

#### 3.2.2 贝叶斯估计法

贝叶斯估计法是一种基于贝叶斯定理的参数估计方法。贝叶斯估计法需要指定先验分布，即参数的先验概率分布。正态分布的先验分布通常为正态分布或逆伽马分布。

MATLAB中使用 `bayesfit` 函数进行贝叶斯估计：

% 指定先验分布
prior = struct('mu', normrnd(0, 1), 'sigma', gamrnd(1, 1));

% 进行贝叶斯估计
params = bayesfit(data, prior, 'distribution', 'normal');

% 获取估计的均值和标准差
mu = params.mu;
sigma = params.sigma;

# 4. 正态分布参数估计的应用

### 4.1 假设检验

正态分布参数估计的一个重要应用是假设检验。假设检验是一种统计方法，用于确定给定的数据是否与某个假设相符。在正态分布参数估计中，假设检验可以用于以下目的：

- **检验均值是否等于特定值：**例如，一家制造商声称其生产的灯泡的平均寿命为 1000 小时。我们可以使用假设检验来确定该声称是否得到数据的支持。
- **检验方差是否等于特定值：**例如，一家公司声称其产品的质量控制过程的标准差为 0.5。我们可以使用假设检验来确定该声称是否得到数据的支持。

假设检验的过程涉及以下步骤：

1. **提出假设：**提出一个关于正态分布参数的假设，例如，均值等于特定值或方差等于特定值。
2. **制定备择假设：**提出一个与假设相反的备择假设，例如，均值不等于特定值或方差不等于特定值。
3. **确定显著性水平：**选择一个显著性水平，通常为 0.05，表示我们愿意接受假设为真的最大错误概率。
4. **计算检验统计量：**根据数据计算一个检验统计量，该统计量衡量数据与假设的偏离程度。
5. **确定临界值：**根据显著性水平和自由度确定临界值。
6. **比较检验统计量和临界值：**如果检验统计量大于临界值，则拒绝假设；否则，接受假设。

### 4.2 置信区间估计

置信区间估计是正态分布参数估计的另一个重要应用。置信区间估计是一种统计方法，用于估计正态分布参数的真实值。置信区间由两个值组成，称为置信区间下限和置信区间上限。置信区间估计的过程涉及以下步骤：

1. **计算样本均值和样本方差：**从数据中计算样本均值和样本方差。
2. **确定置信水平：**选择一个置信水平，通常为 95%，表示我们有 95% 的把握，真实值落在置信区间内。
3. **计算置信区间：**根据样本均值、样本方差、置信水平和自由度计算置信区间。

置信区间估计可以用于以下目的：

- **估计正态分布均值的真实值：**例如，我们可以使用置信区间估计来估计一家制造商生产的灯泡的平均寿命的真实值。
- **估计正态分布方差的真实值：**例如，我们可以使用置信区间估计来估计一家公司质量控制过程的标准差的真实值。

### 4.3 参数敏感性分析

参数敏感性分析是正态分布参数估计的第三个重要应用。参数敏感性分析是一种统计方法，用于确定正态分布参数的变化对其他统计量的影响。参数敏感性分析的过程涉及以下步骤：

1. **选择参数：**选择要分析的正态分布参数，例如，均值或方差。
2. **改变参数值：**在一定范围内改变参数值。
3. **计算其他统计量：**计算其他统计量，例如，置信区间或假设检验的 p 值，对于每个参数值。
4. **绘制敏感性图：**绘制参数值与其他统计量的关系图。

参数敏感性分析可以用于以下目的：

- **确定参数变化对置信区间的影响：**例如，我们可以使用参数敏感性分析来确定均值变化对置信区间宽度的影响。
- **确定参数变化对假设检验结果的影响：**例如，我们可以使用参数敏感性分析来确定方差变化对假设检验的 p 值的影响。

# 5. MATLAB中正态分布参数估计的进阶

### 5.1 正态分布的混合模型

正态分布的混合模型（GMM）是一种概率模型，它假设数据是由多个正态分布的混合而成的。GMM 可以用来对具有多个模式或峰值的数据进行建模。

在 MATLAB 中，可以使用 `fitgmdist` 函数来拟合 GMM。该函数需要数据和混合成分的数量作为输入。

% 数据
data = [1 2 3 4 5 6 7 8 9 10];

% 混合成分的数量
K = 2;

% 拟合 GMM
gm = fitgmdist(data, K);

拟合的 GMM 的参数可以从 `gm` 对象中提取。

% 均值
means = gm.mu;

% 协方差
covariances = gm.Sigma;

% 混合权重
weights = gm.ComponentProportion;

### 5.2 正态分布的非参数估计

正态分布的非参数估计方法不需要假设数据的分布。这些方法通常基于数据的秩或分位数。

在 MATLAB 中，可以使用 `ksdensity` 函数来进行正态分布的非参数估计。该函数需要数据作为输入，并返回估计的概率密度函数。

% 数据
data = [1 2 3 4 5 6 7 8 9 10];

% 非参数估计
[f, x] = ksdensity(data);

估计的概率密度函数可以绘制出来，以可视化数据的分布。

plot(x, f);

### 5.3 正态分布的贝叶斯推断

正态分布的贝叶斯推断是一种使用贝叶斯统计对正态分布的参数进行推断的方法。贝叶斯推断需要先验分布和似然函数作为输入。

在 MATLAB 中，可以使用 `bayesstats` 工具箱来进行正态分布的贝叶斯推断。该工具箱提供了 `bayesfit` 函数，可以拟合各种概率分布的贝叶斯模型。

% 数据
data = [1 2 3 4 5 6 7 8 9 10];

% 先验分布
mu_prior = 5;
sigma_prior = 2;

% 似然函数
likelihood = @(mu, sigma) normpdf(data, mu, sigma);

% 拟合贝叶斯模型
model = bayesfit(data, 'Normal', 'mu_prior', mu_prior, 'sigma_prior', sigma_prior, 'likelihood', likelihood);

拟合的贝叶斯模型的参数可以从 `model` 对象中提取。

% 后验均值
mu_posterior = model.mu_posterior;

% 后验标准差
sigma_posterior = model.sigma_posterior;