MATLAB正态分布置信区间：获取正态分布参数的可靠估计

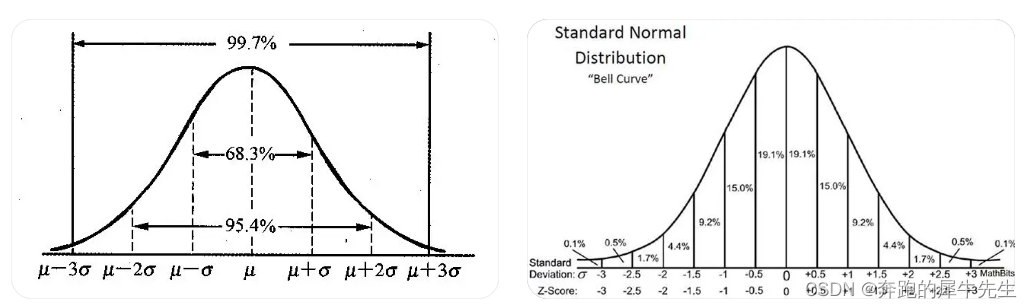
# 1. MATLAB中正态分布简介

正态分布，又称高斯分布，是一种连续概率分布，在自然界和科学研究中广泛存在。其概率密度函数为：

f(x) = (1 / (σ√(2π))) * exp(-(x - μ)² / (2σ²))

其中，μ表示正态分布的均值，σ表示标准差。

正态分布具有以下特点：

- **对称性：**分布曲线关于均值μ对称。
- **钟形曲线：**分布曲线呈钟形，均值μ处取最大值。
- **渐近性：**分布曲线两侧逐渐接近于水平线，即概率密度逐渐减小。

# 2. 正态分布参数估计

### 2.1 最大似然估计

#### 2.1.1 似然函数的构建

似然函数是给定观测数据时，模型参数的函数。在正态分布中，似然函数表示为：

L(μ, σ^2 | x_1, x_2, ..., x_n) = (2πσ^2)^(-n/2) * exp(-∑(x_i - μ)^2 / (2σ^2))

其中：

* μ 是正态分布的均值
* σ^2 是正态分布的方差
* x_1, x_2, ..., x_n 是观测数据

#### 2.1.2 参数估计的求解方法

最大似然估计 (MLE) 是一种通过最大化似然函数来估计模型参数的方法。对于正态分布，MLE 估计值可以解析求解：

**均值估计：**

μ_MLE = (1/n) * ∑x_i

**方差估计：**

σ^2_MLE = (1/(n-1)) * ∑(x_i - μ_MLE)^2

### 2.2 贝叶斯估计

#### 2.2.1 先验分布的选择

贝叶斯估计是一种结合先验分布和观测数据的估计方法。先验分布表示对参数的先验信念。对于正态分布，通常选择共轭先验分布，即：

* 均值先验：正态分布 N(μ_0, σ_0^2)
* 方差先验：逆伽马分布 Inv-Gamma(α, β)

#### 2.2.2 后验分布的推导

结合先验分布和似然函数，可以得到后验分布：

**均值后验：**

μ_post | x_1, x_2, ..., x_n ~ N(μ_n, σ_n^2)

其中：

μ_n = (σ_0^2 * μ_0 + σ^2_MLE * μ_MLE) / (σ_0^2 + σ^2_MLE)
σ_n^2 = (σ_0^2 * σ^2_MLE) / (σ_0^2 + σ^2_MLE)

**方差后验：**

σ^2_post | x_1, x_2, ..., x_n ~ Inv-Gamma(α + n/2, β + ∑(x_i - μ_MLE)^2 / 2)

# 3.1 正态分布置信区间的理论基础

#### 3.1.1 置信水平和置信区间的概念

**置信水平**：

置信水平表示对估计值准确性的信心程度。它通常用百分比表示，例如 95% 或 99%。置信水平越高，对估计值的信心就越大。

**置信区间**：

置信区间是包含估计值的一个区间，有指定置信水平的概率。换句话说，置信区间表示估计值落在该区间内的概率。

#### 3.1.2 正态分布置信区间的公式

对于正态分布，置信区间可以使用以下公式计算：

[μ - z * σ/√n, μ + z * σ/√n]

其中：

* μ 是正态分布的均值
* σ 是正态分布的标准差
* n 是样本量
* z 是与置信水平对应的 z 分位数

例如，对于 95% 的置信水平，z 分位数为 1.96。

### 3.2 MATLAB中置信区间的实现

#### 3.2.1 正态分布参数估计函数

MATLAB 中提