MATLAB正态分布累积分布函数：计算正态分布的累积概率

# 1. 正态分布简介**

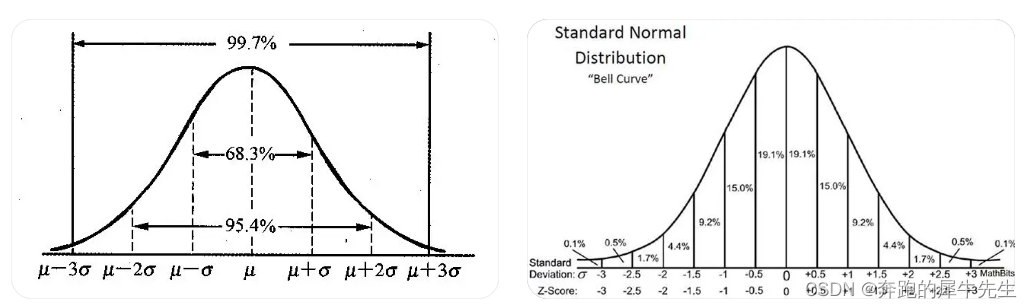
正态分布，也称为高斯分布，是统计学中最常见的连续概率分布之一。它在自然界和科学研究中广泛存在，用于描述许多现象，例如身高、智商和测量误差。

正态分布的概率密度函数为：

f(x) = (1 / (σ√(2π))) * e^(-(x-μ)² / (2σ²))

其中：

* μ 是正态分布的均值，表示分布的中心位置。
* σ 是正态分布的标准差，表示分布的离散程度。

# 2. 正态分布累积分布函数

### 2.1 正态分布累积分布函数的定义和公式

正态分布的累积分布函数（CDF）表示在给定值 x 处分布的概率质量的累积。对于正态分布，CDF 由以下公式给出：

F(x) = ∫_{-∞}^{x} (1 / σ√(2π)) * e^(-(x - μ)² / (2σ²)) dx

其中：

* μ 是分布的均值
* σ 是分布的标准差

### 2.2 正态分布累积分布函数的性质

正态分布的累积分布函数具有以下性质：

* **单调递增：**CDF 随着 x 的增加而单调递增。
* **范围：**CDF 的范围从 0 到 1。
* **对称性：**对于均值为 0 的正态分布，CDF 关于原点对称。
* **正态化：**在整个实数域上，CDF 的积分等于 1。

### 2.3 正态分布累积分布函数的应用

正态分布的累积分布函数在概率论和统计学中有着广泛的应用，包括：

* **概率计算：**给定一个值 x，CDF 可以计算在该值以下的概率。
* **统计推断：**CDF 可用于计算置信区间和假设检验。
* **风险评估：**CDF 可用于评估金融、保险和工程等领域中的风险。

**示例：**

假设一个正态分布的均值为 10，标准差为 2。要计算在 x = 12 处的概率，我们可以使用 CDF 公式：

F(12) = ∫_{-∞}^{12} (1 / 2√(2π)) * e^(-(x - 10)² / (2 * 2²)) dx

使用积分表或数值方法，我们可以计算出 F(12) ≈ 0.8187。这表示在该分布中，x 小于或等于 12 的概率为 81.87%。

# 3.1 normcdf函数的语法和用法

MATLAB中的`normcdf`函数用于计算正态分布的累积分布函数。其语法为：

P = normcdf(X, mu, sigma)

其中：

* `P`：正态分布累积分布函数的值。
* `X`：正态分布中的随机变量。
* `mu`：正态分布的均值。
* `sigma`：正态分布的标准差。

`normcdf`函数的用法非常简单。只需指定正态分布中的随机变量、均值和标准差，即可得到累积分布函数的值。例如，要计算均值为0、标准差为1的正态分布中随机变量X小于1的概率，可以使用以下代码：

P = normcdf(1, 0, 1);

### 3.2 normcdf函数的示例和应用

`normcdf`函数在实际应用中非常广泛，下面是一些示例：

**示例1：计算概率**

假设有一家公司生产的灯泡，其使用寿命服从均值为1000小时、标准差为100小时的正态分布。要计算灯泡使用寿命超过1200小时的概率，可以使用以下代码：

P = normcdf(1