MATLAB正态分布相关性分析：探索正态分布变量之间的关联

# 1. MATLAB中正态分布的理论基础

正态分布，又称高斯分布，是一种常见的概率分布，其概率密度函数为：

f(x) = (1 / (σ√(2π))) * e^(-(x-μ)² / (2σ²))

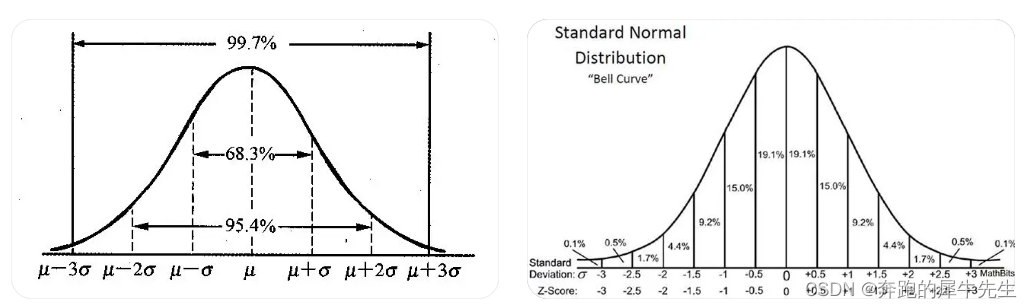
其中，μ表示正态分布的均值，σ表示标准差。正态分布具有以下特点：

- **对称性：**正态分布的概率密度函数关于均值μ对称。
- **钟形曲线：**正态分布的概率密度函数呈钟形曲线，峰值位于均值μ处。
- **面积性质：**正态分布的概率密度函数在均值μ的任意两个点之间的面积等于该区间内概率的总和。

# 2. 正态分布相关性分析的数学原理

### 2.1 协方差和相关系数

#### 2.1.1 协方差的定义和计算

协方差是衡量两个随机变量之间线性关系强度的指标。对于两个随机变量 X 和 Y，其协方差定义为：

Cov(X, Y) = E[(X - μ_X)(Y - μ_Y)]

其中，E 表示期望值，μ_X 和 μ_Y 分别表示 X 和 Y 的均值。

协方差的计算公式为：

Cov(X, Y) = (1/n) Σ[(x_i - μ_X)(y_i - μ_Y)]

其中，n 为样本容量，x_i 和 y_i 分别表示第 i 个样本中 X 和 Y 的值。

#### 2.1.2 相关系数的定义和计算

相关系数是协方差的标准化形式，其范围为[-1, 1]。相关系数定义为：

ρ(X, Y) = Cov(X, Y) / (σ_X σ_Y)

其中，σ_X 和 σ_Y 分别表示 X 和 Y 的标准差。

相关系数的计算公式为：

ρ(X, Y) = (1/n) Σ[(x_i - μ_X)(y_i - μ_Y)] / (σ_X σ_Y)

相关系数的正负号表示 X 和 Y 之间的线性关系方向：

* ρ(X, Y) > 0 表示正相关，即 X 和 Y 同时增大或减小。
* ρ(X, Y) < 0 表示负相关，即 X 增大时 Y 减小，反之亦然。
* ρ(X, Y) = 0 表示不相关，即 X 和 Y 之间没有线性关系。

### 2.2 相关性的统计推断

#### 2.2.1 相关性假设检验

相关性假设检验用于检验两个随机变量之间是否存在显著的线性关系。假设检验过程如下：

1. **提出原假设和备择假设：**
- 原假设：H_0：ρ(X, Y) = 0（X 和 Y 不相关）
- 备择假设：H_1：ρ(X, Y) ≠ 0（X 和 Y 相关）

2. **计算相关系数和检验统计量：**
- 计算样本相关系数 ρ(X, Y)
- 计算检验统计量：t = ρ(X, Y) * √(n - 2) / √(1 - ρ(X, Y)^2)

3. **确定临界值：**
- 查 t 分布表，确定自由度为 n - 2 的双尾临界值 t_α/2

4. **做出决策：**
- 如果 |t| > t_α/2，则拒绝原假设，认为 X 和 Y 相关。
- 否则，接受原假设，认为 X 和 Y 不相关。

#### 2.2.2 置信区间估计

置信区间估计用于估计相关系数的真实值。置信区间估计过程如下：

1. **计算相关系数和标准误：**
- 计算样本相关系数 ρ(X, Y)
- 计算标准误：SE(ρ) = 1 / √(n - 2)

2. **确定置信水平：**
- 选择置信水平，例如 95%

3. **计算置信区间：**
- 计算置信区间：ρ(X, Y) ± t_α/2 * SE(ρ)

其中，t_α/2 是自由度为 n - 2 的双尾临界值。

# 3. MATLAB中正态分布相关性分析的实践