MATLAB正态分布函数初探：解锁数据分析新境界，掌握基本用法与实战示例

# 1. MATLAB正态分布简介**

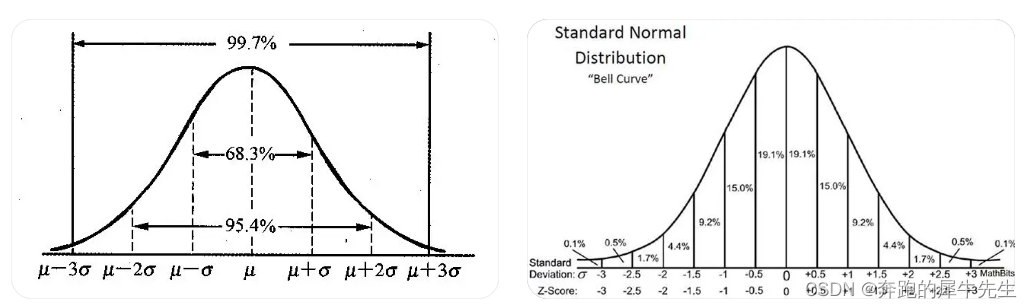
正态分布，又称高斯分布，是一种连续概率分布，在自然界和科学研究中广泛存在。MATLAB中提供了丰富的函数来处理正态分布，包括生成随机数、计算概率密度和累积分布函数等。

正态分布具有钟形曲线形状，其概率密度函数为：

f(x) = (1 / (σ√(2π))) * e^(-(x - μ)² / (2σ²))

其中，μ表示均值，σ表示标准差。正态分布的概率密度函数对称于均值，随着x与均值的距离增加，概率密度迅速下降。

# 2. 正态分布的理论基础

### 2.1 正态分布的定义和特性

正态分布，又称为高斯分布，是一种连续概率分布，其概率密度函数呈钟形曲线。它在自然界和社会科学中广泛存在，描述了许多随机变量的分布，例如身高、体重、测量误差等。

正态分布的数学定义为：

f(x) = (1 / (σ√(2π))) * e^(-(x - μ)² / (2σ²))

其中：

- x：随机变量
- μ：均值，分布的中心位置
- σ：标准差，分布的离散程度

正态分布具有以下特性：

- **对称性：**概率密度函数关于均值对称。
- **单峰性：**概率密度函数在均值处达到最大值。
- **钟形曲线：**概率密度函数呈钟形，两端渐近于 x 轴。
- **面积性质：**在任意两个点 x1 和 x2 之间的面积等于正态分布在该区间内的概率。

### 2.2 正态分布的概率密度函数

正态分布的概率密度函数描述了随机变量取特定值的概率。其数学表达式为：

f(x) = (1 / (σ√(2π))) * e^(-(x - μ)² / (2σ²))

其中：

- x：随机变量
- μ：均值
- σ：标准差

概率密度函数表示在给定均值和标准差的情况下，随机变量取特定值的相对可能性。

**代码块：**

% 定义正态分布参数
mu = 0; % 均值
sigma = 1; % 标准差

% 计算概率密度
x = linspace(-3, 3, 100); % 定义 x 值范围
f = (1 / (sigma * sqrt(2 * pi))) * exp(-(x - mu).^2 / (2 * sigma^2));

% 绘制概率密度函数
plot(x, f);
xlabel('x');
ylabel('概率密度');
title('正态分布的概率密度函数');

**逻辑分析：**

这段代码使用 `linspace` 函数生成一组 x 值，然后使用正态分布的概率密度函数公式计算每个 x 值的概率密度。最后，绘制概率密度函数曲线。

**参数说明：**

- `mu`：正态分布的均值
- `sigma`：正态分布的标准差
- `x`：随机变量的值
- `f`：概率密度

### 2.3 正态分布的累积分布函数

正态分布的累积分布函数 (CDF) 给出了随机变量小于或等于特定值的概率。其数学表达式为：

F(x) = (1 / 2) * (1 + erf((x - μ) / (σ√(2))))

其中：

- x：随机变量
- μ：均值
- σ：标准差
- erf()：误差函数

**代码块：**

% 定义正态分布参数
mu = 0; % 均值
sigma = 1; % 标准差

% 计算累积分布函数
x = linspace(-3, 3, 100); % 定义 x 值范围
F = (1 / 2) * (1 + erf((x - mu) / (sigma * sqrt(2))));

% 绘制累积分布函数
plot(x, F);
xlabel('x');
ylabel('累积概率');
title('正态分布的累积分布函数');

**逻辑分析：**

这段代码使用 `linspace` 函数生成一组 x 值，然后使用正态分布的累积分布函数公式计算每个 x 值的累积概率。最后，绘制累积分布函数曲线。

**参数说明：**

- `mu`：正态分布的均值
- `sigma`：正态分布的标准差
- `x`：随机变量的值
- `F`：累积概率

# 3. MATLAB中正态分布函数的使用

### 3.1 正态分布随机数的生成

在MATLAB中，可以使用`randn`函数生成正态分布的随机数。`randn`函数的语法如下：

X = randn(m, n)

其中：

* `m`：生成的随机数矩阵的行数
* `n`：生成的随机数矩阵的列数

例如，以下代码生成一个5行3列的正态分布随机数矩阵：

X = randn(5, 3);

### 3.2 正态分布概率密度的计算

在MATLAB中，可以使用`normpdf`函数计算正态分布的概率密度。`normpdf`函数的语法如下：

y = normpdf(x, mu, sigma)

其中：

* `x`：要计算概率密度的值
* `mu`：正态分布的均值
* `sigma`：正态分布的标准差

例如，以下代码计算值为0、均值为1、标准差为2的正态分布的概率密度：

x = 0;
mu = 1;
sigma = 2;
y = normpdf(x, mu, sigma);

### 3.3 正态分布累积分布函数的计算

在MATLAB中，可以使用`normcdf`函数计算正态分布的累积分布函数。`normcdf`函数的语法如下：

y = normcdf(x, mu, sigma)

其中：

* `x`：要计算累积分布函数的值
* `mu`：正态分布的均值
* `sigma`：正态分布的标准差

例如，以下代码计算值为0、均值为1、标准差为2的正态分布的累积分布函数：

x = 0;
mu = 1;
sigma = 2;
y = normcdf(x, mu, sigma);

# 4. 正态分布函数在数据分析中的应用

### 4.1 数据拟合和模型选择

正态分布函数在数据分析中有着广泛的应用，其中一个重要的应用是数据拟合和模型选择。数据拟合是指找到一个数学模型来描述给定数据集的趋势和模式。正态分布函数是一种常用的概率模型，可以用来拟合各种类型的数据。

**数据拟合步骤：**

1. **假设正态分布：**首先假设数据服从正态分布。
2. **估计参数：**使用最大似然估计或其他方法估计正态分布的参数，包括均值和标准差。
3. **计算拟合优度：**使用拟合优度指标（如 R² 或 AIC）评估拟合模型的优度。
4. **比较模型：**如果有多个拟合模型，比较它们的拟合优度，选择最优模型。

### 4.2 假设检验和置信区间估计

正态分布函数还可以用于假设检验和置信区间估计。

**假设检验：**

假设检验是一种统计推断方法，用于确定给定数据是否支持某个假设。正态分布函数可以用来计算样本均值或其他统计量的 p 值，从而帮助确定假设是否被拒绝。

**置信区间估计：**

置信区间估计是一种统计推断方法，用于估计未知参数的范围。正态分布函数可以用来计算样本均值或其他统计量的置信区间，从而获得参数估计值的置信度。

### 代码示例

**数据拟合：**

% 生成正态分布数据
data = normrnd(5, 1, 100);

% 拟合正态分布模型
pd = fitdist(data, 'Normal');

% 计算拟合优度
R2 = corr(data, pd.random(100))^2;
disp(['拟合优度 (R²): ', num2str(R2)]);

% 可视化拟合结果
figure;
histogram(data, 'Normalization', 'probability');
hold on;
x = linspace(min(data), max(data), 100);
y = pdf(pd, x);
plot(x, y, 'r', 'LineWidth', 2);
xlabel('数据值');
ylabel('概率密度');
title('数据拟合结果');
legend('数据分布', '拟合模型');

**假设检验：**

% 生成正态分布数据
data = normrnd(5, 1, 100);

% 定义假设
H0: mu = 5
Ha: mu ≠ 5

% 计算样本均值和标准差
sample_mean = mean(data);
sample_std = std(data);

% 计算 t 统计量
t_stat = (sample_mean - 5) / (sample_std / sqrt(length(data)));

% 计算 p 值
p_value = 2 * tcdf(abs(t_stat), length(data) - 1);

% 确定是否拒绝 H0
if p_value < 0.05
    disp('拒绝 H0，存在显著差异');
else
    disp('不拒绝 H0，没有显著差异');
end

**置信区间估计：**

% 生成正态分布数据
data = normrnd(5, 1, 100);

% 计算样本均值和标准差
sample_mean = mean(data);
sample_std = std(data);

% 计算置信区间
alpha = 0.05;
z_alpha_2 = norminv(1 - alpha / 2);
CI = sample_mean +/- z_alpha_2 * sample_std / sqrt(length(data));

% 显示置信区间
disp(['置信区间：', num2str(CI(1)), ', ', num2str(CI(2))]);

# 5. 正态分布函数的实战示例

### 5.1 数据拟合和正态性检验

#### 数据拟合

正态分布函数可以用来拟合数据，以确定数据是否服从正态分布。MATLAB 中提供了 `fitdist` 函数，可以对数据进行正态分布拟合。

% 加载数据
data = load('data.mat');

% 正态分布拟合
[params, gof] = fitdist(data, 'Normal');

% 输出拟合参数
disp('拟合参数：');
disp(params);

% 输出拟合优度
disp('拟合优度：');
disp(gof);

`fitdist` 函数返回拟合参数和拟合优度。拟合参数包括正态分布的均值和标准差，而拟合优度则衡量拟合的质量。

#### 正态性检验

正态性检验可以确定数据是否服从正态分布。MATLAB 中提供了 `lillietest` 函数，可以进行正态性检验。

% 正态性检验
[h, p] = lillietest(data);

% 输出检验结果
if h == 1
    disp('数据不符合正态分布。');
else
    disp('数据符合正态分布。');
end

`lillietest` 函数返回两个值：`h` 和 `p`。`h` 为 1 表示数据不符合正态分布，`h` 为 0 表示数据符合正态分布。`p` 为 p 值，表示拒绝原假设（数据服从正态分布）的概率。

### 5.2 假设检验和置信区间估计

#### 假设检验

正态分布函数可以用于假设检验，以确定数据是否满足特定的假设。例如，我们可以检验数据是否来自具有特定均值或标准差的正态分布。

% 假设检验：均值
[h, p, ci, stats] = ttest(data, 0);

% 输出检验结果
if h == 1
    disp('数据均值与 0 存在显著差异。');
else
    disp('数据均值与 0 没有显著差异。');
end

% 输出置信区间
disp('置信区间：');
disp(ci);

`ttest` 函数返回 `h`、`p`、`ci` 和 `stats` 四个值。`h` 为 1 表示拒绝原假设（数据均值等于 0），`h` 为 0 表示接受原假设。`p` 为 p 值，表示拒绝原假设的概率。`ci` 为置信区间，表示数据均值的估计范围。`stats` 为检验统计量和自由度等统计信息。

#### 置信区间估计

正态分布函数也可以用于置信区间估计，以估计数据的未知参数。例如，我们可以估计数据均值或标准差的置信区间。

% 置信区间估计：均值
[mu, sigma] = normfit(data);
[ci, ~] = normconf(0.95, mu, sigma);

% 输出置信区间
disp('均值置信区间：');
disp(ci);

`normfit` 函数返回正态分布的均值和标准差估计值。`normconf` 函数返回置信区间，表示数据均值的估计范围。置信水平为 0.95，表示我们有 95% 的把握，数据均值落在置信区间内。

# 6. MATLAB正态分布函数的进阶应用**

### 6.1 多元正态分布

多元正态分布是正态分布在多维空间上的推广，其概率密度函数为：

f(x) = (2π)^(-p/2) |Σ|^(-1/2) exp(-1/2 (x - μ)^T Σ^(-1) (x - μ))

其中：

* x 是 p 维随机向量
* μ 是 p 维均值向量
* Σ 是 p × p 协方差矩阵

在 MATLAB 中，可以使用 `mvnrnd` 函数生成多元正态分布的随机数，语法为：

X = mvnrnd(mu, Sigma, n)

其中：

* mu 是 p 维均值向量
* Sigma 是 p × p 协方差矩阵
* n 是要生成的随机数的个数

### 6.2 非正态分布数据的处理

当数据不符合正态分布时，可以使用以下方法进行处理：

* **变换：** 使用 Box-Cox 变换或对数变换等方法将非正态分布的数据转换为正态分布。
* **非参数检验：** 使用秩和检验或卡方检验等非参数检验方法，它们不依赖于数据分布的假设。
* **稳健统计：** 使用中位数或四分位数等稳健统计量，它们对异常值不敏感。

在 MATLAB 中，可以使用以下函数进行非正态分布数据的处理：

* **boxcox：** Box-Cox 变换
* **log：** 对数变换
* **ranksum：** 秩和检验
* **chi2gof：** 卡方检验
* **median：** 中位数
* **iqr：** 四分位数