Python拓扑图数据结构案例研究：项目实现与策略分析

# 1. Python拓扑图数据结构概述

## 简介
拓扑图数据结构是计算机科学领域中用于表示元素之间关系的一种抽象数据类型。在Python中，这一数据结构尤其重要，因为它在处理复杂数据关系时具有高度的灵活性和表达能力。例如，在构建网络路由、任务调度、数据流分析等场景中，拓扑图数据结构常常发挥关键作用。

## 应用背景
在软件开发过程中，我们经常需要分析和优化数据流程或对象间的关系。Python语言因其简洁的语法和强大的库支持，在处理这类问题时显得尤为得心应手。利用Python实现的拓扑图数据结构，可以帮助开发者以直观和高效的方式解决问题，从而提升整体的开发效率和代码质量。

## 结构特点
拓扑图由节点（顶点）和边（弧）组成，边代表节点之间的关系。在Python中，这可以通过多种方式实现，例如使用列表（list）和字典（dict）组合表示图，或创建更高级的类结构来封装图的操作。无论是哪种方法，都要求其易于扩展和维护，且能有效地支持相关算法的实现，如拓扑排序和关键路径分析。

接下来的章节将深入探讨Python如何实现拓扑图数据结构、相关算法的编码实现，以及在实际项目中的应用案例。

# 2. 拓扑图数据结构的理论基础

## 2.1 图论的基本概念

### 2.1.1 图的定义和分类

图论是数学的一个分支，它研究的是图形的性质和图形之间的关系。在图论中，图（Graph）是由顶点（Vertices）集合和边（Edges）集合构成的。在Python中，顶点和边可以是任何类型的数据和它们之间的关系，例如社交网络中的用户和他们之间的友情关系。

根据边是否有方向，图可以分为无向图（Undirected Graph）和有向图（Directed Graph）。无向图中的边是没有方向性的，表示顶点之间的一种关系。而在有向图中，边是有方向性的，表示从一个顶点到另一个顶点的关系。

另外，根据边是否可以连接同一个顶点，图也可以分为简单图（Simple Graph）和多重图（Multigraph）。在简单图中，任意两个顶点之间最多只有一条边，且不允许顶点自身相连。多重图允许顶点之间有多条边，甚至允许顶点自身与自己相连。

### 2.1.2 图的表示方法

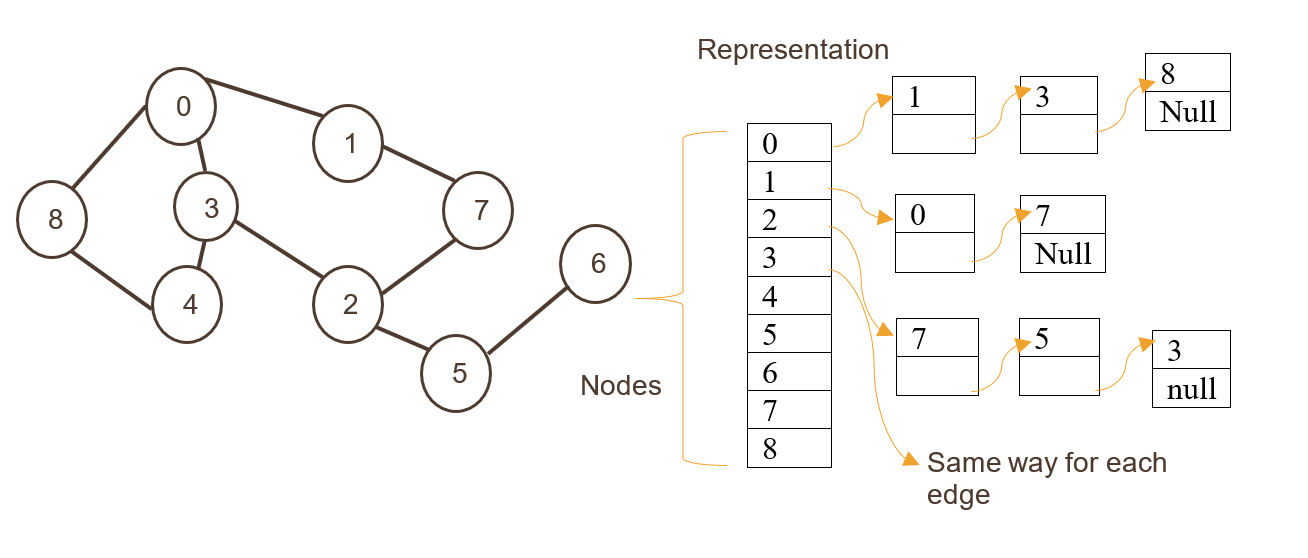
图可以用多种方式来表示，最常见的是邻接矩阵（Adjacency Matrix）和邻接表（Adjacency List）。

邻接矩阵是一个二维数组，其大小为顶点数的平方。矩阵中的元素表示顶点间的边。对于无向图来说，邻接矩阵是对称的；而对于有向图，邻接矩阵可以是非对称的。

邻接表是一种列表的列表，其中每个顶点有一个相关的列表，这个列表包含了从该顶点出发的所有边。

在Python实现图时，可以使用字典和列表来表示邻接表。例如，使用字典的键值对表示顶点及其相邻顶点的列表：

graph = {
    'A': ['B', 'C'],
    'B': ['D', 'E'],
    'C': ['F'],
    'D': [],
    'E': ['F'],
    'F': []
}

## 2.2 拓扑排序的理论基础

### 2.2.1 拓扑排序的定义和意义

拓扑排序是针对有向无环图（DAG）的一种排序方式。它会返回一个顶点的线性序列，这个序列满足图中的每条有向边的箭头方向，即图中存在一条从顶点U到顶点V的边时，顶点U在序列中会在顶点V之前。

拓扑排序在很多领域都有应用，比如课程表的安排、任务依赖关系的处理等。在项目管理中，它可以帮助我们确定任务执行的先后顺序，以避免出现执行依赖上的冲突。

### 2.2.2 拓扑排序算法的原理

拓扑排序的核心算法是Kahn算法。其基本思想是：首先找出所有入度为0的顶点（即没有任何前置任务的顶点），然后把这些顶点放入结果列表中，并从图中删除这些顶点及其相关联的边。之后，再次寻找入度为0的顶点，重复上述操作，直到图中没有顶点为止。

如果图中有环存在，拓扑排序会失败，因为存在环意味着至少有一个顶点的入度不可能为0。

def topological_sort(graph):
    # 计算所有顶点的入度
    in_degree = {v: 0 for v in graph}
    for u in graph:
        for v in graph[u]:
            in_degree[v] += 1
    # 找出所有入度为0的顶点
    zero_in_degree = [v for v in graph if in_degree[v] == 0]
    sorted_order = []
    while zero_in_degree:
        u = zero_in_degree.pop(0)
        sorted_order.append(u)
        # 对于顶点u的每个邻接点v，将其入度减1
        for v in graph[u]:
            in_degree[v] -= 1
            # 如果入度减到0，则加入到队列中
            if in_degree[v] == 0:
                zero_in_degree.append(v)
    if len(sorted_order) != len(graph):
        raise Exception("Graph has a cycle!")
    return sorted_order

## 2.3 关键路径分析法

### 2.3.1 关键路径的定义和性质

关键路径是另一种用于有向无环图的路径分析方法。关键路径定义为从起始顶点到结束顶点的最长路径。这个路径上没有松弛的时间，即这条路径上的所有任务必须按照严格的顺序执行，不能有任何延迟。如果任务延迟，整个项目就无法按时完成。

关键路径可以帮助我们找出项目中的关键任务（那些不能延迟的任务），从而有效管理项目的时间和资源。

### 2.3.2 关键路径算法的实现步骤

关键路径算法（Critical Path Method，CPM）的关键步骤包括：

1. 计算每个顶点的最早开始时间（earliest start time, EST）和最迟开始时间（latest start time, LST）。
2. 计算每条边的最早开始时间和最迟开始时间。
3. 确定关键活动，即那些最早开始时间和最迟开始时间相等的活动。

关键路径上的所有活动都具有零松弛时间，即活动的最早开始时间和最迟开始时间相等。

def find_earliest_start_times(graph):
    earliest_start = {v: 0 for v in graph}
    for u in graph:
        for v in graph[u]:
            earliest_start[v] = max(earliest_start[v], earliest_start[u] + 1)
    return earliest_start

def find_latest_start_times(graph, earliest_start):
    latest_start = {v: earliest_start[v] for v in graph}
    changed = True
    while changed:
        changed = False
        for u in graph:
            for v in graph[u]:
                if latest_start[v] > earliest_start[v]:
                    continue
                latest_start[v] = min(latest_start[v], latest_start[u] - 1)
                changed = True
    return latest_start

def find_critical_path(graph):
    earliest_start = find_earliest_start_times(graph)
    latest_start = find_latest_start_times(graph, earliest_start)
    critical_path = []
    for u in graph:
        for v in graph[u]:
            if earliest_start[u] + 1 == latest_start[v]:
                critical_path.append((u, v))
    return critical_path

以上代码展示了如何计算关键路径，关键在于计算每个顶点的最早开始时间和最迟开始时间，并据此确定关键路径上的边。

# 3. Python拓扑图数据结构的实现方法

## 3.1 Python中的图结构实现

### 3.1.1 利用字典和列表实现图

在Python中实现图结构时，我们可以选择多种数据结构来表示。字典（`dict`）和列表（`list`）是两种常用的结构，它们能够简单高效地表示图的节点和边。

这里我们将讨论如何使用Python内置的`dict`和`list`来表示无向图和有向图。

#### 无向图的实现：

无向图中，节点之间是双向连接，意味着如果我们有两个节点A和B，那么存在一条边将它们连接。

# 无向图实现示例

# 使用字典来保存图的边，键为边的一个节点，值为另一个节点（假设没有重复边）
graph = {
    'A': ['B', 'C'],
    'B': ['A', 'D', 'E'],
    'C': ['A', 'F'],
    'D': ['B'],
    'E': ['B', 'F'],
    'F': ['C', 'E']
}

# 为了遍历图中的所有节点，我们可以通过访问字典的键来获取
for node in graph:
    print(node)  # A B C D E F

# 为了访问节点B的邻居，我们可以通过访问字典中键为B的值来获取
print(graph['B'])  # ['A', 'D', 'E']

#### 有向图的实现：

有向图中，节点之间的连接是有方向的，意味着边(A, B)不等于边(B, A)。

# 有向图实现示例

# 使用字典来保存图的边，键为起始节点，值为一个列表，表示连接到的节点
directed_graph = {
    'A': ['B', 'C'],
    'B': ['D', 'E'],
    'C': ['F'],
    'D': [],
    'E': ['F'],
    'F': []
}

# 遍历图中的所有节点
for node in directed_graph:
    print(node)  # A B C D E F

# 为了找出从节点A出发可以到达的所有节点，我们可以查看字典中键为A的值
print(directed_graph['A'])  # ['B', 'C']

### 3.1.2 图类的设计和封装

为了更好地封装图的功能，并提供接口给其他对象或模块使用，我们可以创建一个图类。这里我们使用Python的面向对象编程来实现。

class Graph:
    def __init