从零开始构建图数据结构：Python实现大全

# 1. 图数据结构的理论基础

图数据结构是计算机科学中的一个核心概念，它通过顶点（节点）和边的集合来表示实体间的关系。图的广泛应用覆盖了社交网络分析、交通规划、生物信息学等多个领域。理解图的基本理论是深入学习图算法与图数据结构优化的前提。本章节将为读者系统地介绍图的基本概念、分类，以及图理论在实际应用中的基础作用。

## 2.1 图的基本概念

### 2.1.1 图的定义

在数学中，图是由顶点集合V和边集合E组成的抽象数据类型，边可以是有向或无向的，图可以被表示为G=(V, E)。图的每一条边连接了两个顶点，表示它们之间存在某种特定的关系。图的这种表示方式非常适合描述实体间的复杂关系。

### 2.1.2 图的分类

图根据其边的特性可以分为无向图和有向图。无向图的边没有方向性，连接的两个顶点地位平等；而有向图的边具有方向，表明了一个顶点到另一个顶点的关系。此外，还有完全图、稀疏图、带权图等特殊类型的图，每一种类型在不同的应用场合有着不同的意义和作用。

接下来的章节将通过具体的Python代码演示图的表示方法，为读者深入理解图数据结构和图算法打下坚实的基础。

# 2. 图的Python基础表示

图是一种基础的数据结构，用于表示实体之间复杂的关系。在Python中，图可以通过多种方式表示，包括邻接矩阵、邻接表和边列表。本章节将分别介绍这些表示方法，并展示如何用Python实现。

## 2.1 图的基本概念

### 2.1.1 图的定义
在计算机科学和数学中，图是由节点（顶点）和连接节点的边组成的集合。节点可以看作是实体，边表示这些实体之间的某种关系。图可以是有向的也可以是无向的，这取决于边是否具有方向性。如果边有方向，那么这个图就是有向图，否则就是无向图。

### 2.1.2 图的分类
图根据其特性可以分为多种类型：
- 无向图：边无方向性。
- 有向图：边有方向性。
- 加权图：边带有权重，用于表示边的“成本”或“距离”。
- 非加权图：边没有权重。

## 2.2 图的Python表示方法

在Python中，可以通过多种方式表示图，以下为三种常见的实现方法。

### 2.2.1 邻接矩阵
邻接矩阵是一种表示图的矩阵表示法，其中行和列分别代表图中的顶点。如果顶点i和顶点j之间存在边，则矩阵的(i, j)元素为1（对于无权图），或边的权重（对于加权图）。否则，元素为0。

# 邻接矩阵示例
class Graph:
    def __init__(self, vertices):
        self.V = vertices
        self.graph = [[0 for column in range(vertices)]
                      for row in range(vertices)]

    def add_edge(self, u, v, weight=1):
        self.graph[u][v] = weight
        self.graph[v][u] = weight  # 无向图

# 实例化图对象
g = Graph(5)
g.add_edge(0, 1)
g.add_edge(0, 4)
g.add_edge(1, 2)
g.add_edge(1, 3)
g.add_edge(1, 4)
g.add_edge(2, 3)
g.add_edge(3, 4)

### 2.2.2 邻接表
邻接表是一种更加节省空间的图表示方法，特别适合表示稀疏图。它使用一个字典来存储每个顶点及其相邻顶点的列表。

# 邻接表示例
class Graph:
    def __init__(self, vertices):
        self.V = vertices
        self.graph = [[] for _ in range(vertices)]

    def add_edge(self, u, v):
        self.graph[u].append(v)  # 无向图

# 实例化图对象
g = Graph(5)
g.add_edge(0, 1)
g.add_edge(0, 4)
g.add_edge(1, 2)
g.add_edge(1, 3)
g.add_edge(1, 4)
g.add_edge(2, 3)
g.add_edge(3, 4)

### 2.2.3 边列表
边列表使用一个列表的元组表示所有的边，每个元组包含一对顶点。它通常用于有向图，但也可以用于无向图。

# 边列表示例
edges = [(0, 1), (0, 4), (1, 2), (1, 3), (1, 4), (2, 3), (3, 4)]

每种表示方法都有其特定的用例和优缺点。选择哪种方法取决于图的类型和应用场景。接下来的章节将会深入探讨图的遍历算法实现，包括深度优先搜索（DFS）和广度优先搜索（BFS）。

# 3. 图的遍历算法实现

## 3.1 深度优先搜索(DFS)

### 3.1.1 DFS的原理

深度优先搜索（DFS，Depth-First Search）是一种用于遍历或搜索树或图的算法。该算法沿着树的分支进行深度探索，直到达到某个节点的所有可能分支都被遍历为止，然后回溯到上一个节点继续探索其他分支。在图中，DFS通常使用递归或栈实现。

### 3.1.2 使用递归实现DFS

递归是实现DFS的直观方法，算法从一个起始节点开始，探索尽可能深的分支，直到分支的末端，然后回溯到前一个节点继续探索新的分支。

以下是使用Python实现DFS的递归示例代码：

def dfs_recursive(graph, start, visited=None):
    if visited is None:
        visited = set()
    visited.add(start)
    print(start)  # 可以替换为对节点的其他处理逻辑
    for next_node in graph[start] - visited:
        dfs_recursive(graph, next_node, visited)
    return visited

# 示例图
graph = {
    'A': {'B', 'C'},
    'B': {'A', 'D', 'E'},
    'C': {'A', 'F'},
    'D': {'B'},
    'E': {'B', 'F'},
    'F': {'C', 'E'}
}

# 执行DFS
dfs_recursive(graph, 'A')

在这个递归实现中，`graph`是一个字典，表示图的邻接表形式，键为节点，值为与该节点相连的节点集合。`start`是遍历的起始节点。`visited`集合用来记录已经访问过的节点，防止重复访问。

### 3.1.3 使用栈实现DFS

使用栈的DFS实现模拟了递归过程，但避免了递归可能引起的栈溢出问题。它通过显式地使用栈数据结构来追踪接下来要访问的节点。

以下是一个使用栈实现DFS的示例代码：

def dfs_with_stack(graph, start):
    visited = set()
    stack = [start]
    while stack:
        node = stack.pop()
        if node not in visited:
            print(node)
            visited.add(node)
            stack.extend(graph[node] - visited)
    return visited

# 使用与上面递归实现相同的图示例
dfs_with_stack(graph, 'A')

在这个实现中，我们用一个栈`stack`来存储要访问的节点。算法首先将起始节点压入栈中。在每次循环中，我们从栈中弹出一个节点，检查它是否已经被访问过。如果没有，我们打印出它，然后将它的所有未访问邻居压入栈中。这个过程一直进行，直到栈为空。

## 3.2 广度优先搜索(BFS)

### 3.2.1 BFS的原理

广度优先搜索（BFS，Breadth-First Search）是另一种用于遍历或搜索树或图的算法。它从根节点开始，逐层遍历每个节点的所有邻居，直到找到目标节点或遍历完所有节点。BFS使用队列数据结构来保持访问节点的顺序。

### 3.2.2 使用队列实现BFS

以下是使用Python实现BFS的示例代码：

from collections import deque

def bfs_with_queue(graph, start):
    visited = set()
    queue = deque([start])
    while queue:
        node = queue.popleft()
        if node not in visited:
            print(node)
            visited.add(node)
            queue.extend(graph[node] - visited)
    return visited

# 使用与上面DFS实现相同的图示例
bfs_with_queue(graph, 'A')

在这个实现中，我们使用`deque`从`collections`模块作为队列。算法首先将起始节点加入队列。在每次循环中，我们从队列的左端弹出一个节点，检查它是否已经被访问过。如果没有，我们打印出它，然后将它的所有未访问邻居加入队列的右端。这个过程一直进行，直到队列为空。

### 3.2.3 BFS的应用场景分析

BFS在多种应用场景中非常有用，例如：

- **最短路径问题**：在无权图中，BFS可以找到从一个节点到另一个节点的最短路径（最少边数的路径）。
- **层序遍历**：在树的遍历中，BFS可以按层访问所有节点，这在层次结构分析中非常有用。
- **网络爬虫**：在网站或网络结构的遍历中，BFS可以按层次逐步爬取网页或资源。

## 3.3 图的遍历算法应用场景

图的遍历算法在多个领域有着广泛的应用。例如，在社交网络分析中，可以通过遍历算法分析节点间的关系和社区结构。在导航系统中，通过图的遍历可以找到两地之间的最短路径。在计算机网络中，可以使用这些算法检测网络中的环和故障。

应用图遍历算法时，需要考虑图的表示方法、算法的复杂度以及是否适用于特定的图类型。在实际应用中，可能还需要对算法进行优化，比如通过并行计算加速处理或利用启发式信息减少搜索空间。

# 4. 图的高级算法与优化

## 4.1 最短路径算法

### 4.1.1 Dijkstra算法

Dijkstra算法是图论中解决单源最短路径问题的经典算法。它适用于带权重的有向图和无向图，但权重不能为负值。Dijkstra算法的原理是贪心算法，通过逐步扩展已知的最短路径来寻找整个图的最短路径。

假设我们要找从源点A到点B的最短路径，算法的基本步骤如下：
1. 初始化源点A到其他所有点的距离为无穷大，到自己的距离为0。
2. 创建一个集合S，包含所有距离已知的顶点。
3. 对于集合S中的每一个顶点，更新其邻接点的距离。如果新的路径比当前记录的路径短，则更新。
4. 从未处理的顶点集合中选取距离源点最近的顶点，并将其加入集合S。
5. 重复步骤3和4，直到所有顶点都被处理。

下面是一个简单的Dijkstra算法的Python实现示例：

import heapq

def dijkstra(graph, start):
    # 初始化距离表，所有节点距离设置为无穷大
    distances = {vertex: float('infinity') for vertex in graph}
    # 源点到自身的距离为0
    distances[start] = 0
    # 优先队列，用于选择当前距离最小的节点
    priority_queue = [(0, start)]
    while priority_queue:
        # 弹出最小距离节点
        current_distance, current_vertex = heapq.heappop(priority_queue)
        # 遍历当前节点的邻接点
        for neighbor, weight in graph[current_vertex].items():
            distance = current_distance + weight
            # 如果计算出的距离小于已知距离，则进行更新
            if distance < distances[neighbor]:
                distances[neighbor] = distance
                heapq.heappush(priority_queue, (distance, neighbor))
    return distances

# 示例图
graph = {
    'A': {'B': 1, 'C': 4},
    'B': {'A': 1, 'C': 2, 'D': 5},
    'C': {'A': 4, 'B': 2, 'D': 1},
    'D': {'B': 5, 'C': 1}
}

# 计算从A点到其他点的最短路径
print(dijkstra(graph, 'A'))

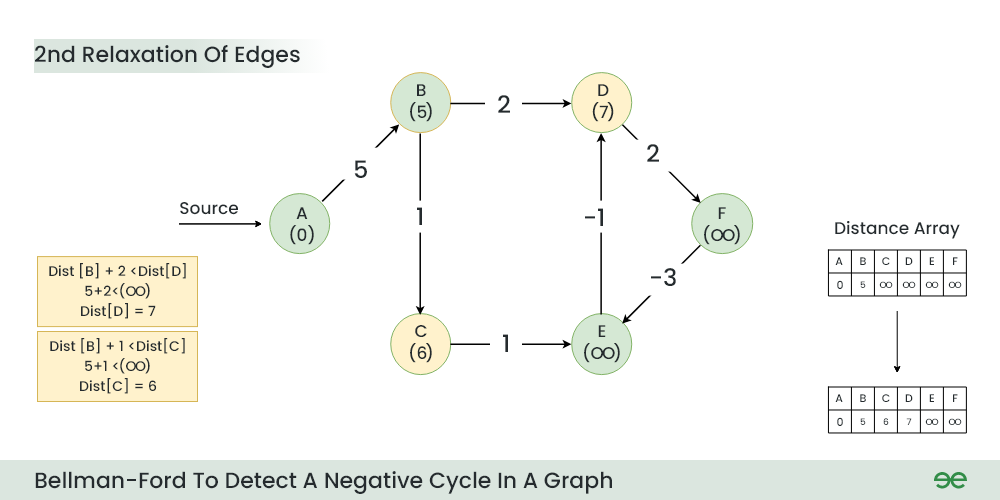
### 4.1.2 Bellman-Ford算法

Bellman-Ford算法是另一种用于计算单源最短路径的算法，相比Dijkstra算法，它可以处理图中存在负权重边的情况。Bellman-Ford算法的核心思想是，对于每一条边，如果存在更短的路径，则更新路径长度。

算法基本步骤如下：
1. 初始化源点到其他所有点的距离为无穷大，源点到自己的距离为0。
2. 对图中的每条边进行V-1次松弛操作（V是顶点的数量）。每次遍历所有的边，如果当前边可以减少到目标点的已知最短路径，那么更新这个最短路径。
3. 检查图中是否存在负权重环路。对于每条边，再次尝试松弛操作，如果还能减少距离，则说明存在负权重环路。

下面是Bellman-Ford算法的Python实现：

def bellman_ford(graph, start):
    distances = {vertex: float('infinity') for vertex in graph}
    distances[start] = 0
    # 松弛操作V-1次
    for _ in range(len(graph) - 1):
        for vertex in graph:
            for neighbor, weight in graph[vertex].items():
                if distances[vertex] != float('infinity') and \
                   distances[vertex] + weight < distances[neighbor]:
                    distances[neighbor] = distances[vertex] + weight
    # 检测负权重环路
    for vertex in graph:
        for neighbor, weight in graph[vertex].items():
            if distances[vertex] != float('infinity') and \
               distances[vertex] + weight < distances[neighbor]:
                print("Graph contains a negative-weight cycle")
                return None
    return distances

# 示例图，与Dijkstra算法示例相同
print(bellman_ford(graph, 'A'))

### 4.1.3 Floyd-Warshall算法

Floyd-Warshall算法是用来寻找所有顶点对之间最短路径的算法。与Dijkstra和Bellman-Ford不同，Floyd-Warshall算法考虑了所有顶点之间的最短路径，适用于较小规模的图。

Floyd-Warshall算法的主要步骤如下：
1. 初始化一个距离矩阵，距离矩阵的大小为顶点数乘以顶点数，初始时对角线元素为0（表示顶点到自身的距离），其余为无穷大（表示顶点之间没有直接的路径）。
2. 对于每一对顶点(u, v)，更新所有可能的中间顶点k，如果通过顶点k能够缩短u到v的距离，则更新这个距离。
3. 通过动态规划的方法更新这个距离矩阵。

下面是一个Floyd-Warshall算法的Python实现示例：

def floyd_warshall(graph):
    distances = {u: {v: graph.get((u, v), float('infinity')) for v in graph} for u in graph}
    nodes = list(distances.keys())
    # 更新距离矩阵
    for k in nodes:
        for i in nodes:
            for j in nodes:
                distances[i][j] = min(distances[i][j], distances[i][k] + distances[k][j])
    return distances

# 示例图
graph = {
    ('A', 'B'): 1, ('A', 'C'): 4,
    ('B', 'A'): 1, ('B', 'C'): 2, ('B', 'D'): 5,
    ('C', 'A'): 4, ('C', 'B'): 2, ('C', 'D'): 1,
    ('D', 'B'): 5, ('D', 'C'): 1
}

# 计算所有顶点对之间的最短路径
distances = floyd_warshall(graph)
for i in distances:
    print(distances[i])

## 4.2 最小生成树算法

### 4.2.1 Kruskal算法

Kruskal算法是用于在加权无向图中找到最小生成树的贪心算法。最小生成树是指在一个加权连通图中找到一个边的子集，使得子集中的边构成的树包含了图中的所有顶点，并且边的权重之和最小。

算法步骤如下：
1. 将所有的边按权重从小到大排序。
2. 初始化一个空的最小生成树。
3. 遍历排序后的边列表，对于每条边，如果它连接的两个顶点在最小生成树中还没有被连接，就将它加入最小生成树。
4. 重复步骤3直到最小生成树中有V-1条边（V是顶点的数量）。

下面是一个Kruskal算法的Python实现示例：

class DisjointSet:
    def __init__(self, vertices):
        self.vertices = vertices
        self.parent = {vertex: vertex for vertex in vertices}
        self.rank = {vertex: 0 for vertex in vertices}
    def find(self, item):
        if self.parent[item] != item:
            self.parent[item] = self.find(self.parent[item])
        return self.parent[item]
    def union(self, set1, set2):
        root1 = self.find(set1)
        root2 = self.find(set2)
        if root1 != root2:
            if self.rank[root1] > self.rank[root2]:
                self.parent[root2] = root1
            else:
                self.parent[root1] = root2
                if self.rank[root1] == self.rank[root2]:
                    self.rank[root2] += 1

def kruskal(graph):
    # 初始化顶点集
    vertices = list(graph.keys())
    # 初始化边集合，并进行排序
    edges = [(weight, start, end) for start, adj in graph.items() for end, weight in adj.items()]
    edges.sort()
    # 初始化最小生成树
    mst = []
    # 初始化不连通的顶点集合
    ds = DisjointSet(vertices)
    # 遍历所有边
    for weight, start, end in edges:
        # 如果当前边连接的两个顶点不在同一个集合中，添加到最小生成树
        if ds.find(start) != ds.find(end):
            ds.union(start, end)
            mst.append((start, end, weight))
    return mst

# 示例图
graph = {
    'A': {'B': 1, 'C': 4},
    'B': {'A': 1, 'C': 2, 'D': 5},
    'C': {'A': 4, 'B': 2, 'D': 1},
    'D': {'B': 5, 'C': 1}
}

print(kruskal(graph))

### 4.2.2 Prim算法

Prim算法是另一种找到加权无向图中最小生成树的算法。Prim算法从一个顶点开始，逐步扩大最小生成树的规模，直到包含所有顶点。

算法步骤如下：
1. 从一个顶点开始，初始化最小生成树为空。
2. 找到当前最小生成树的边中，连接未包含在最小生成树中的顶点的最小权重的边，并将这个边和顶点加入最小生成树。
3. 重复步骤2，直到最小生成树中包含了所有顶点。

下面是一个Prim算法的Python实现示例：

import heapq

def prim(graph, start):
    # 初始化优先队列和距离表
    priority_queue = [(weight, start, end) for end, weight in graph[start].items()]
    heapq.heapify(priority_queue)
    visited = set(graph.keys())
    mst = []
    while priority_queue:
        weight, u, v = heapq.heappop(priority_queue)
        if v not in visited:
            visited.add(v)
            mst.append((u, v, weight))
            for neighbor, weight in graph[v].items():
                if neighbor not in visited:
                    heapq.heappush(priority_queue, (weight, v, neighbor))
    return mst

# 示例图
print(prim(graph, 'A'))

## 4.3 算法优化策略

### 4.3.1 时间复杂度分析

时间复杂度是衡量算法效率的重要指标。以Dijkstra算法为例，如果没有使用优先队列，其时间复杂度为O(V^2)，其中V是顶点的数量。使用优先队列（例如最小堆）可以将时间复杂度降低到O((V+E)logV)，其中E是边的数量。而Bellman-Ford算法的时间复杂度为O(VE)，适用于边数较多的情况。Kruskal算法的时间复杂度为O(ElogE)，主要由于需要对所有边进行排序。Prim算法的时间复杂度与Kruskal相似，也是O(ElogE)。

### 4.3.2 空间复杂度分析

空间复杂度衡量的是算法运行所需的存储空间。大多数图算法的空间复杂度主要取决于顶点和边的数量。例如，Dijkstra和Bellman-Ford算法需要存储到每个顶点的距离和前驱顶点信息，因此空间复杂度为O(V)。而Floyd-Warshall算法由于需要保存所有顶点对之间的最短路径，空间复杂度为O(V^2)。

### 4.3.3 实际问题中的优化实例

在实际应用中，图算法优化需要考虑多个方面，包括但不限于数据结构的选择、图的预处理、并行计算等。例如，在使用Dijkstra算法时，若对优先队列中的元素进行批处理而不是单个处理，可以减少比较的次数，提高效率。对于大型图的处理，可以将图数据存储在硬盘上，并使用外部排序和分块读取技术来减少内存消耗。此外，可以利用现代多核处理器，通过并行化某些操作（如BFS的层级处理）来加快算法的执行速度。

# 5. 图数据结构的实践项目

图数据结构不仅在理论上具有丰富的内涵，而且在实践中也拥有广泛的应用场景。本章节将深入探讨图数据结构在实践项目中的具体应用，为读者呈现图结构如何在现实世界中解决复杂问题。

## 5.1 网络路由模拟

网络路由模拟是图数据结构应用的一个典型例子，其核心在于模拟网络结构的图构建，实现高效的路由算法，并对性能进行评估。

### 5.1.1 模拟网络结构的图构建

构建网络路由模拟的关键在于将真实世界的网络转换成图的形式。在这个图中，节点可以代表路由器、交换机或任何网络中的结点，而边则代表连接这些结点的线路或信道。

#### 代码实现网络图构建

下面是一个简化的例子，我们用Python来构建一个网络图：

class Graph:
    def __init__(self):
        self.graph = {}
    def add_vertex(self, vertex):
        if vertex not in self.graph:
            self.graph[vertex] = []
    def add_edge(self, v1, v2):
        self.add_vertex(v1)
        self.add_vertex(v2)
        self.graph[v1].append(v2)
        self.graph[v2].append(v1)

# 创建一个图实例
network_graph = Graph()

# 添加网络中的节点
for vertex in ["Router1", "Router2", "Router3", "Router4"]:
    network_graph.add_vertex(vertex)

# 添加节点间的边，表示连接
network_graph.add_edge("Router1", "Router2")
network_graph.add_edge("Router2", "Router3")
network_graph.add_edge("Router1", "Router3")
network_graph.add_edge("Router1", "Router4")

在上述代码中，我们首先定义了一个`Graph`类，该类包含了一个字典`graph`，用于存储图中所有节点及其关联的边。通过`add_vertex`方法添加节点，通过`add_edge`方法添加边。实际的网络路由模拟可能需要考虑带宽、延迟、成本等因素，但此段代码提供了一个构建图的基本框架。

### 5.1.2 路由算法的实现

路由算法的核心目标是找到从源节点到目标节点的最短或最佳路径。在图的表示基础上，我们可以使用多种图算法来实现路由功能，例如Dijkstra算法和Bellman-Ford算法。

#### 代码实现Dijkstra算法

Dijkstra算法是解决单源最短路径问题的常用算法。以下为Dijkstra算法的Python实现：

import heapq

def dijkstra(graph, start):
    distances = {vertex: float('infinity') for vertex in graph.graph}
    distances[start] = 0
    priority_queue = [(0, start)]
    while priority_queue:
        current_distance, current_vertex = heapq.heappop(priority_queue)
        for neighbor in graph.graph[current_vertex]:
            distance = current_distance + 1
            if distance < distances[neighbor]:
                distances[neighbor] = distance
                heapq.heappush(priority_queue, (distance, neighbor))
    return distances

distances = dijkstra(network_graph, "Router1")
print(distances)

在此代码段中，我们首先为图中的每个节点设置了无穷大的距离，并将起点的距离设为0。接着，使用一个优先队列（最小堆）来实现算法。每次从优先队列中弹出当前距离最小的节点，更新其邻居的距离。最终，`distances`字典中包含了从起点到所有节点的最短路径距离。

### 5.1.3 性能评估

对于路由算法而言，除了计算出正确的结果，算法的性能也是一个重要的考量因素。性能评估通常会考虑算法的计算复杂度和实际运行时间。

#### 性能分析

Dijkstra算法的时间复杂度为O((V+E)logV)，其中V是顶点数，E是边数。在图数据结构较大时，算法效率会受到明显影响。优化的策略包括使用更加高效的数据结构，或者针对特定类型的图进行算法改进。

## 5.2 社交网络分析

社交网络分析是图数据结构应用的另一个重要领域。在这个领域，节点通常代表个人或实体，边则代表他们之间的关系或交互。

### 5.2.1 社交网络的图表示

在社交网络中，图的表示通常需要反映用户之间的关注关系、朋友关系或其他互动关系。

#### 代码实现社交网络图

以下是一个简化的社交网络图表示的Python实现：

class SocialGraph(Graph):
    def __init__(self):
        super().__init__()
    def add Friendship(self, user1, user2):
        self.add_edge(user1, user2)

# 创建一个社交网络图实例
social_graph = SocialGraph()

# 添加社交网络中的用户和他们的友谊关系
social_graph.add友谊("Alice", "Bob")
social_graph.add友谊("Bob", "Charlie")
social_graph.add友谊("Charlie", "Dave")
social_graph.add友谊("Alice", "Dave")

在这段代码中，我们扩展了`Graph`类以创建`SocialGraph`类，专门用于社交网络的图表示。通过`add友谊`方法添加节点之间的边，代表两个用户之间的友谊关系。

### 5.2.2 影响力最大节点的寻找

在社交网络中，寻找影响力最大的节点（如名人、意见领袖）是一个常见问题。这通常可以通过计算节点的度（即与节点相连的边的数量）来实现。

#### 度中心性算法

度中心性算法是一种简单直观的方法，用于识别网络中影响力大的节点。计算公式为：节点度数/网络中节点的总数。

def calculate_degree_centrality(graph):
    centrality = {}
    for vertex in graph.graph:
        centrality[vertex] = len(graph.graph[vertex])
    max_centrality = max(centrality.values())
    for vertex in centrality:
        centrality[vertex] /= max_centrality
    return centrality

centrality_scores = calculate_degree_centrality(social_graph)
print(centrality_scores)

在这个代码段中，我们定义了一个`calculate_degree_centrality`函数，计算每个节点的度中心性，并返回一个包含中心性分数的字典。通过比较这些分数，我们可以找到影响力最大的用户。

### 5.2.3 社交圈的社区检测

社区检测是分析社交网络中用户群体结构的一种方法，旨在发现网络中的自然分区或社区。

#### 模块度优化算法

模块度优化算法是检测社区的一种常用方法。算法旨在将图划分为多个模块（社区），使得同一模块内部的边密度较大，而不同模块之间的边密度较小。

由于社区检测算法通常较为复杂，这里仅提供一个概念性的框架：

def community_detection(graph):
    # 这里是一个伪代码，实际实现需要更复杂的算法和数据结构
    communities = []
    # 算法逻辑，比如使用贪心算法或其他策略来识别社区
    return communities

社区检测算法的实现通常涉及到图的遍历、边的重新分配等操作，是图算法中的一个高级主题。

通过上述章节的介绍，我们展示了图数据结构在模拟网络路由和社交网络分析中的应用。这仅是图数据结构在实践中应用的冰山一角。在未来的章节中，我们将继续探索图数据结构在现实世界中的应用，如交通网络分析和生物信息学应用。

# 6. 图数据结构在现实世界的应用

图数据结构不仅在计算机科学和理论算法中占有一席之地，而且在现实世界的应用中也扮演着极为重要的角色。从城市的交通网络，到社交网络的影响力分析，再到生物信息学的基因网络探索，图的应用无处不在。

## 6.1 交通网络分析

交通网络是现实世界中图数据结构的一个典型应用。在城市中，道路、铁路、航线等都可以用图的边来表示，而交汇点则可以作为图的节点。通过图的数据结构，可以进行多种交通分析。

### 6.1.1 城市交通网络的图构建

构建一个城市的交通网络图，首先需要确定图中的节点和边。节点代表交通网络中的交汇点，如交通灯、十字路口、公交站等；边代表连接两个交汇点的道路段，可以是有向边（如单行道），也可以是无向边（如双向道路）。每条边都可以带有一个权重，表示通过该路段所需的时间、距离或其他成本。

下面是一个简单的Python代码示例，使用邻接矩阵构建一个城市交通网络的图：

# 城市交通网络图的邻接矩阵表示
graph = [
    [0, 1, 0, 0, 0],
    [1, 0, 1, 1, 0],
    [0, 1, 0, 1, 1],
    [0, 1, 1, 0, 1],
    [0, 0, 1, 1, 0]
]

# 节点表示：0-城市中心，1-东区，2-南区，3-西区，4-北区

### 6.1.2 路径规划算法应用

路径规划算法在交通网络分析中至关重要。通过图的遍历和最短路径算法，可以找到从一个节点到另一个节点的最短路径，这对于导航系统和物流运输尤为重要。

# 使用Dijkstra算法寻找最短路径的示例代码

def dijkstra(graph, start):
    distances = {vertex: float('infinity') for vertex in graph}
    distances[start] = 0
    priority_queue = [(0, start)]
    while priority_queue:
        current_distance, current_vertex = heapq.heappop(priority_queue)

        if current_distance > distances[current_vertex]:
            continue
        for neighbor, weight in enumerate(graph[current_vertex]):
            distance = current_distance + weight

            if distance < distances[neighbor]:
                distances[neighbor] = distance
                heapq.heappush(priority_queue, (distance, neighbor))
    return distances

### 6.1.3 交通拥堵的预测分析

通过图模型可以分析交通网络中的瓶颈区域，预测交通拥堵的情况，并提出改进措施。例如，通过模拟特定时间段内各路段的流量，可以发现哪些路段最有可能出现拥堵，并据此优化交通信号控制和规划新的道路建设。

# 交通拥堵预测分析伪代码
def predict_traffic_congestion(graph, traffic_data):
    congestion_points = []
    for node in graph:
        for neighbor, weight in enumerate(node):
            # 使用traffic_data和当前交通流量数据进行分析
            # 如果达到拥堵标准，则将该节点加入到congestion_points列表
            pass
    return congestion_points

# traffic_data表示各时间段内各路段的交通流量数据

## 6.2 生物信息学中的应用

在生物信息学领域，图数据结构同样有着广泛的应用。基因网络、蛋白质相互作用网络等都可以用图来表示。这些图结构对于研究生物系统、疾病诊断和药物研发等有着重要的意义。

### 6.2.1 基因网络的图表示

基因网络可以表示为一个图，其中的节点代表基因，边代表基因之间的相互作用。这种图可以用来研究生物体中基因如何相互作用，从而影响生物体的生理和病理过程。

### 6.2.2 生物路径的图搜索

在生物信息学中，研究人员可以利用图的搜索算法来寻找基因或蛋白质之间的路径，从而了解不同生物学功能之间的关系。这些路径可能关联到特定的生物过程，例如细胞信号传导、代谢途径等。

# 生物路径搜索的示例代码
def find_biological_path(graph, start_gene, end_gene):
    # 使用广度优先搜索(BFS)来寻找一条从start_gene到end_gene的路径
    pass

### 6.2.3 药物研发中的图算法应用

在药物研发中，研究人员需要了解药物分子与蛋白质相互作用的复杂网络。通过图算法，可以分析药物分子如何影响特定的生物路径，从而促进新药的发现和疾病治疗方案的改进。

# 药物研发中的图算法应用示例代码
def drug_target_interaction(graph, drug, protein):
    # 分析药物分子drug和蛋白质protein之间的相互作用
    pass

通过上述应用案例可以看出，图数据结构在处理和分析复杂网络结构时提供了一种强大的工具。无论是交通系统规划、社交网络分析，还是生物信息学的研究，图数据结构都能够提供深入洞察，并支持决策过程。随着数据科学和人工智能技术的发展，图数据结构的应用将变得更加广泛和高效。