揭秘算法数据结构：掌握基础，进阶算法设计（附实战案例分析）

# 1. 算法和数据结构基础**

算法和数据结构是计算机科学的基础，它们是解决复杂问题的关键工具。算法是一系列步骤，用于解决特定问题，而数据结构是一种组织和存储数据的方式，以便高效地访问和操作。

算法和数据结构的理解对于任何希望在IT行业取得成功的专业人士来说都是至关重要的。它们是解决现实世界问题、优化代码性能和设计高效系统的基础。通过掌握算法和数据结构，您可以提高您的问题解决能力，并为您的职业生涯奠定坚实的基础。

# 2.1 贪心算法

### 2.1.1 贪心算法的原理和应用

贪心算法是一种基于局部最优决策的算法设计方法，它通过在每一步中选择当前最优的局部解，逐步逼近全局最优解。贪心算法的优点在于其简单易懂，时间复杂度较低，并且在某些特定问题上能够得到最优解。

贪心算法的典型应用场景包括：

- **活动选择问题：**给定一系列活动，每个活动有开始时间和结束时间，求最多能参加的活动数量。
- **背包问题：**给定一个背包容量和一系列物品，每个物品有重量和价值，求放入背包中价值最大的物品组合。
- **哈夫曼编码：**给定一系列字符及其出现频率，求最优的编码方案，使得编码后的平均长度最短。

### 2.1.2 贪心算法的局限性

虽然贪心算法简单高效，但它也存在一定的局限性：

- **局部最优不等于全局最优：**贪心算法只考虑当前局部最优决策，可能导致无法得到全局最优解。
- **贪心算法不具备自纠错能力：**一旦在某一步做出错误决策，后续决策也将受到影响，难以纠正错误。

因此，在使用贪心算法时，需要仔细分析问题，确定贪心算法是否适用。如果贪心算法不适用，则需要考虑其他算法设计方法。

**代码示例：**

def activity_selection(activities):
    """
    活动选择问题贪心算法

    :param activities: 活动列表，每个活动包含开始时间和结束时间
    :return: 最多能参加的活动数量
    """
    # 按活动结束时间排序
    activities.sort(key=lambda x: x[1])

    selected_activities = []
    last_activity_end_time = -1

    for activity in activities:
        if activity[0] >= last_activity_end_time:
            selected_activities.append(activity)
            last_activity_end_time = activity[1]

    return len(selected_activities)

**代码逻辑分析：**

1. 首先，将活动列表按结束时间排序，这样可以确保在选择活动时，始终选择结束时间最早的活动。
2. 初始化一个空列表 `selected_activities` 来存储已选择的活动，以及一个变量 `last_activity_end_time` 来记录上一个已选择活动的结束时间。
3. 遍历活动列表，对于每个活动，检查其开始时间是否大于或等于上一个已选择活动的结束时间。如果满足条件，则将该活动添加到 `selected_activities` 中，并更新 `last_activity_end_time` 为该活动的结束时间。
4. 最后，返回 `selected_activities` 的长度，即最多能参加的活动数量。

**参数说明：**

- `activities`：活动列表，每个活动是一个元组，包含开始时间和结束时间。
- `last_activity_end_time`：上一个已选择活动的结束时间。

# 3.1 数组和链表

#### 3.1.1 数组和链表的存储结构

**数组**

数组是一种线性数据结构，其中元素按顺序存储在连续的内存位置中。每个元素都有一个唯一的索引，用于访问它。数组的存储结构如下：

[元素1, 元素2, ..., 元素n]

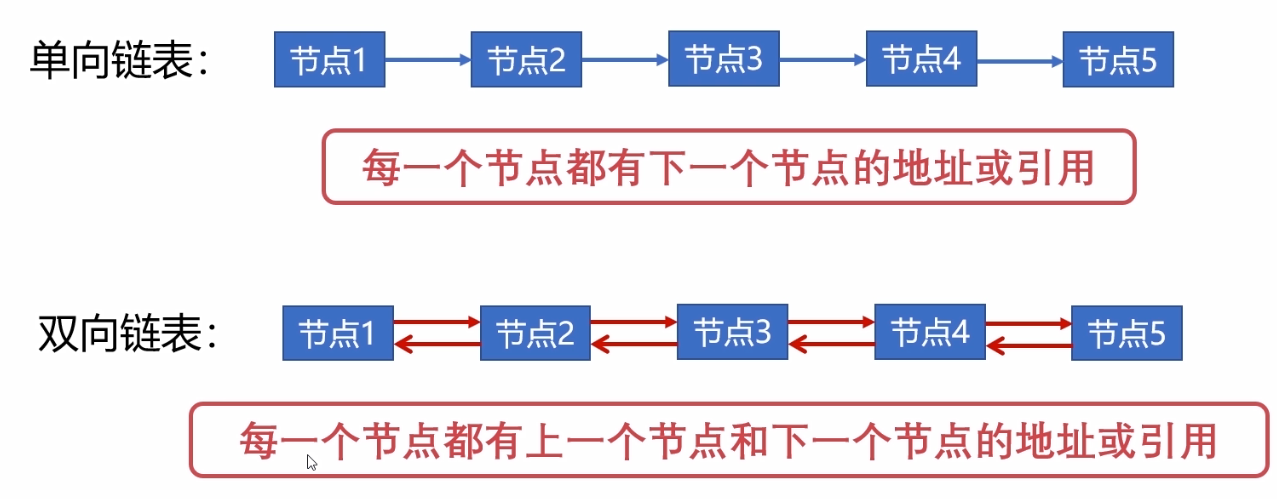
**链表**

链表是一种线性数据结构，其中元素存储在不连续的内存位置中。每个元素包含数据和指向下一个元素的指针。链表的存储结构如下：

{数据1, 指针1} -> {数据2, 指针2} -> ... -> {数据n, NULL}

#### 3.1.2 数组和链表的性能比较

**访问元素**

* 数组：通过索引直接访问，时间复杂度为 O(1)。
* 链表：需要遍历链表直到找到元素，时间复杂度为 O(n)，其中 n 是链表中的元素数量。

**插入元素**

* 数组：需要移动现有元素以腾出空间，时间复杂度为 O(n)。
* 链表：只需更新指针，时间复杂度为 O(1)。

**删除元素**

* 数组：需要移动现有元素以填补空位，时间复杂度为 O(n)。
* 链表：只需更新指针，时间复杂度为 O(1)。

**其他操作**

* 数组：查找元素需要遍历整个数组，时间复杂度为 O(n)。
* 链表：查找元素需要遍历链表直到找到元素，时间复杂度为 O(n)。

**表 3.1 数组和链表性能比较**

| 操作 | 数组 | 链表 |
|---|---|---|
| 访问元素 | O(1) | O(n) |
| 插入元素 | O(n) | O(1) |
| 删除元素 | O(n) | O(1) |
| 查找元素 | O(n) | O(n) |

# 4.1 回溯算法

### 4.1.1 回溯算法的原理和应用

回溯算法是一种深度优先搜索算法，它通过系统地枚举所有可能的解空间来寻找问题的解。回溯算法的基本思想是：

1. **选择一个初始状态：**从问题的初始状态开始。
2. **探索当前状态：**生成当前状态的所有可能的后续状态。
3. **递归调用：**对每个后续状态，递归地调用回溯算法。
4. **回溯：**如果当前状态不满足约束条件，则回溯到上一个状态并尝试其他后续状态。
5. **找到解：**如果当前状态满足约束条件，则返回该状态作为解。

回溯算法广泛应用于求解组合优化问题，例如：

- **旅行商问题：**找到访问一组城市的最短路径，同时每个城市只能访问一次。
- **背包问题：**从一组物品中选择物品，使总价值最大化，同时不超过背包容量。
- **数独：**填充一个 9x9 的网格，使得每一行、每一列和每个 3x3 的子网格中都包含数字 1 到 9。

### 4.1.2 回溯算法的时间复杂度分析

回溯算法的时间复杂度取决于问题的大小和搜索空间的大小。对于一个具有 n 个状态和 b 个分支因子的问题，回溯算法的时间复杂度为 O(n^b)。

例如，对于旅行商问题，有 n 个城市，每个城市有 b 条可能的路径，因此时间复杂度为 O(n^b)。

为了优化回溯算法的时间复杂度，可以采用以下策略：

- **剪枝：**在搜索过程中，如果某个状态不满足约束条件，则直接跳过该状态的后续状态。
- **启发式：**使用启发式函数来引导搜索，优先探索更有可能包含解的状态。
- **并行化：**将搜索过程并行化，以减少整体运行时间。

**代码块：**

def backtrack(state):
    """
    回溯算法求解组合优化问题。

    参数：
        state: 当前状态。
    """

    # 如果当前状态满足约束条件，则返回解
    if is_solution(state):
        return state

    # 生成当前状态的所有后续状态
    next_states = generate_next_states(state)

    # 递归调用回溯算法
    for next_state in next_states:
        solution = backtrack(next_state)
        if solution is not None:
            return solution

    # 回溯
    return None

**代码逻辑分析：**

该代码块实现了回溯算法的基本步骤：

- 检查当前状态是否满足约束条件，如果是则返回解。
- 生成当前状态的所有后续状态。
- 对每个后续状态，递归调用回溯算法。
- 如果找到解，则返回解。
- 如果没有找到解，则回溯到上一个状态并尝试其他后续状态。

**参数说明：**

- `state`：当前状态。

# 5.1 图形路径规划

### 5.1.1 图形路径规划问题描述

图形路径规划问题是指在给定的图形中，寻找从一个起点到一个终点的最优路径。最优路径可以根据不同的标准定义，例如最短路径、最少时间路径或最少成本路径。

图形路径规划问题在现实生活中有着广泛的应用，例如：

- **导航系统：**在导航系统中，需要找到从起点到目的地的最短路径。
- **物流配送：**在物流配送中，需要找到从仓库到客户的最佳配送路径。
- **网络路由：**在网络路由中，需要找到从源节点到目标节点的最优路径。

### 5.1.2 图形路径规划算法

解决图形路径规划问题的算法有很多，常用的算法包括：

- **Dijkstra 算法：**Dijkstra 算法是一种贪心算法，它通过迭代地选择权重最小的边来构造从起点到其他所有顶点的最短路径。
- **Bellman-Ford 算法：**Bellman-Ford 算法是一种动态规划算法，它通过迭代地更新顶点的最短距离来找到从起点到所有其他顶点的最短路径。
- **Floyd-Warshall 算法：**Floyd-Warshall 算法是一种动态规划算法，它通过计算所有顶点对之间的最短路径来找到从任意起点到任意终点的最短路径。

**代码块：Dijkstra 算法**

def dijkstra(graph, start):
    """
    Dijkstra 算法求解图形最短路径

    参数：
        graph: 图形，用邻接矩阵表示
        start: 起点

    返回：
        到所有顶点的最短距离
    """

    # 初始化距离和已访问标记
    distance = [float('inf')] * len(graph)
    visited = [False] * len(graph)

    # 起点距离为 0
    distance[start] = 0

    # 循环，直到所有顶点都被访问
    while not all(visited):
        # 找到未访问顶点中距离最小的顶点
        min_distance = float('inf')
        min_vertex = -1
        for i in range(len(graph)):
            if not visited[i] and distance[i] < min_distance:
                min_distance = distance[i]
                min_vertex = i

        # 标记该顶点已访问
        visited[min_vertex] = True

        # 更新其他顶点的距离
        for i in range(len(graph)):
            if graph[min_vertex][i] > 0 and not visited[i]:
                new_distance = distance[min_vertex] + graph[min_vertex][i]
                if new_distance < distance[i]:
                    distance[i] = new_distance

    return distance

**逻辑分析：**

Dijkstra 算法使用贪心策略，每次选择权重最小的边来更新顶点的最短距离。算法从起点开始，不断迭代，直到所有顶点都被访问。在每次迭代中，算法找到未访问顶点中距离最小的顶点，并更新其他顶点的距离。

**参数说明：**

- `graph`：图形，用邻接矩阵表示。
- `start`：起点。

**返回：**

- 到所有顶点的最短距离。

**代码块：Bellman-Ford 算法**

def bellman_ford(graph, start):
    """
    Bellman-Ford 算法求解图形最短路径

    参数：
        graph: 图形，用邻接表表示
        start: 起点

    返回：
        到所有顶点的最短距离
    """

    # 初始化距离
    distance = [float('inf')] * len(graph)
    distance[start] = 0

    # 循环 |V| - 1 次
    for _ in range(len(graph) - 1):
        # 遍历所有边
        for u in graph:
            for v, weight in graph[u]:
                # 更新距离
                if distance[v] > distance[u] + weight:
                    distance[v] = distance[u] + weight

    # 检查是否存在负权重环
    for u in graph:
        for v, weight in graph[u]:
            if distance[v] > distance[u] + weight:
                raise ValueError("存在负权重环")

    return distance

**逻辑分析：**

Bellman-Ford 算法使用动态规划策略，通过迭代地更新顶点的最短距离来找到从起点到所有其他顶点的最短路径。算法循环 |V| - 1 次，在每次迭代中，算法遍历所有边，并更新顶点的最短距离。如果存在负权重环，算法将抛出异常。

**参数说明：**

- `graph`：图形，用邻接表表示。
- `start`：起点。

**返回：**

- 到所有顶点的最短距离。

**代码块：Floyd-Warshall 算法**

def floyd_warshall(graph):
    """
    Floyd-Warshall 算法求解所有顶点对之间的最短路径

    参数：
        graph: 图形，用邻接矩阵表示

    返回：
        所有顶点对之间的最短路径
    """

    # 初始化距离矩阵
    distance = [[float('inf')] * len(graph) for _ in range(len(graph))]

    # 初始化下一跳矩阵
    next_hop = [[None] * len(graph) for _ in range(len(graph))]

    # 初始化对角线元素
    for i in range(len(graph)):
        distance[i][i] = 0

    # 填充距离矩阵
    for i in range(len(graph)):
        for j in range(len(graph)):
            if graph[i][j] > 0:
                distance[i][j] = graph[i][j]
                next_hop[i][j] = j

    # Floyd-Warshall 算法
    for k in range(len(graph)):
        for i in range(len(graph)):
            for j in range(len(graph)):
                if distance[i][j] > distance[i][k] + distance[k][j]:
                    distance[i][j] = distance[i][k] + distance[k][j]
                    next_hop[i][j] = next_hop[i][k]

    return distance, next_hop

**逻辑分析：**

Floyd-Warshall 算法使用动态规划策略，通过计算所有顶点对之间的最短路径来找到从任意起点到任意终点的最短路径。算法循环 |V| 次，在每次迭代中，算法计算所有顶点对之间的最短路径。如果存在更短的路径，算法将更新距离矩阵和下一跳矩阵。

**参数说明：**

- `graph`：图形，用邻接矩阵表示。

**返回：**

- 所有顶点对之间的最短路径。

# 6. 算法数据结构学习建议**

**6.1 学习资源推荐**

* **书籍：**
* 《算法导论》（第 4 版） - Thomas H. Cormen、Charles E. Leiserson、Ronald L. Rivest、Clifford Stein
* 《数据结构与算法分析》（第 4 版） - Mark Allen Weiss
* **在线课程：**
* Coursera：算法（斯坦福大学）
* edX：数据结构和算法（麻省理工学院）
* **网站：**
* LeetCode：算法和数据结构题库
* GeeksforGeeks：算法和数据结构教程

**6.2 学习方法建议**

* **循序渐进：**从基础算法和数据结构开始，逐步深入到更高级的主题。
* **实践至上：**通过解决算法和数据结构问题来巩固理解。
* **多维度学习：**结合书籍、在线课程和网站等多种资源学习。
* **注重理解：**不要只记住算法和数据结构的实现，更要理解其原理和应用场景。
* **参加竞赛：**参加编程竞赛可以提高算法和数据结构的解决问题能力。

**6.3 常见问题解答**

* **如何选择合适的算法？**
* 考虑问题的类型、输入规模和时间/空间复杂度要求。
* **如何优化算法性能？**
* 使用更有效率的数据结构，优化算法实现，并考虑算法的并行化。
* **如何调试算法？**
* 使用调试工具，如断点和打印语句，逐步检查算法的执行。
* **如何学习算法数据结构？**
* 坚持学习，多练习，并寻求指导和支持。