字符串算法：深入理解字符串处理技术（附算法实现代码）

# 1. 字符串基础**

字符串是计算机科学中一种基本的数据类型，它由一系列字符组成。字符串处理算法是用于操作和分析字符串的算法，在各种应用程序中都有着广泛的应用。

本节将介绍字符串的基础知识，包括字符串的表示、操作和比较。我们将讨论字符串的编码方案、字符串的存储和表示方式，以及字符串的比较和排序算法。

# 2. 字符串处理算法

### 2.1 字符串匹配算法

字符串匹配算法是字符串处理中的一类重要算法，用于在给定文本中查找特定模式或子串。

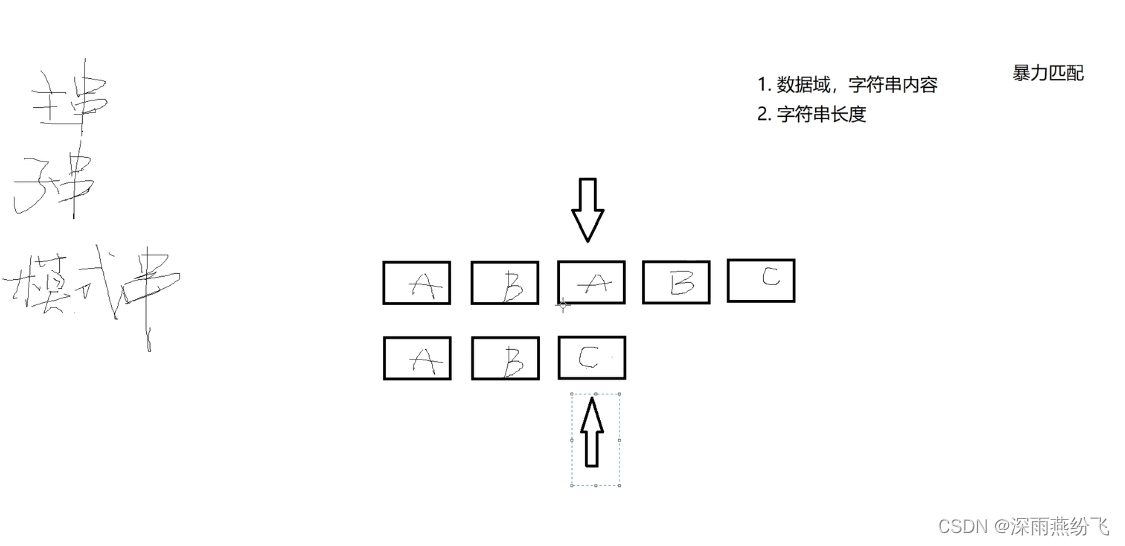
#### 2.1.1 朴素字符串匹配算法

朴素字符串匹配算法是一种简单直接的算法，通过逐个字符比较模式串和文本串来查找匹配项。

**算法流程：**

1. 初始化模式串长度 `m` 和文本串长度 `n`。
2. 对于文本串中每个字符 `i`（从 0 到 `n-m`）：
- 将模式串与文本串中从 `i` 到 `i+m-1` 的子串进行比较。
- 如果匹配成功，则返回 `i`。
3. 如果没有匹配项，则返回 -1。

**代码实现：**

def naive_string_matching(text, pattern):
    """
    朴素字符串匹配算法

    Args:
        text (str): 文本串
        pattern (str): 模式串

    Returns:
        int: 匹配位置（从 0 开始），如果没有匹配项则返回 -1
    """
    m = len(pattern)
    n = len(text)

    for i in range(n - m + 1):
        if text[i:i+m] == pattern:
            return i

    return -1

**逻辑分析：**

该算法的时间复杂度为 O(mn)，其中 m 是模式串长度，n 是文本串长度。算法逐个字符比较模式串和文本串，因此时间复杂度与文本串长度成正比。

#### 2.1.2 KMP算法

KMP算法（Knuth-Morris-Pratt算法）是一种改进的字符串匹配算法，它使用一个称为前缀函数的预处理表来提高匹配效率。

**算法流程：**

1. 预处理模式串，生成前缀函数 `pi`。
2. 初始化模式串长度 `m` 和文本串长度 `n`。
3. 初始化模式串匹配位置 `j` 为 0。
4. 对于文本串中每个字符 `i`（从 0 到 `n-1`）：
- 如果 `j` 大于 0 且文本串第 `i` 个字符与模式串第 `j` 个字符不匹配，则将 `j` 更新为 `pi[j-1]`。
- 如果文本串第 `i` 个字符与模式串第 `j` 个字符匹配，则将 `j` 加 1。
5. 如果 `j` 等于 `m`，则匹配成功，返回 `i-m+1`。
6. 如果遍历完文本串，则没有匹配项，返回 -1。

**代码实现：**

def kmp_string_matching(text, pattern):
    """
    KMP字符串匹配算法

    Args:
        text (str): 文本串
        pattern (str): 模式串

    Returns:
        int: 匹配位置（从 0 开始），如果没有匹配项则返回 -1
    """
    m = len(pattern)
    n = len(text)

    # 预处理模式串，生成前缀函数
    pi = compute_prefix_function(pattern)

    j = 0
    for i in range(n):
        while j > 0 and pattern[j] != text[i]:
            j = pi[j-1]
        if pattern[j] == text[i]:
            j += 1
        if j == m:
            return i - m + 1

    return -1

def compute_prefix_function(pattern):
    """
    计算前缀函数

    Args:
        pattern (str): 模式串

    Returns:
        list[int]: 前缀函数
    """
    m = len(pattern)
    pi = [0] * m

    j = 0
    for i in range(1, m):
        while j > 0 and pattern[j] != pattern[i]:
            j = pi[j-1]
        if pattern[j] == pattern[i]:
            j += 1
        pi[i] = j

    return pi

**逻辑分析：**

KMP算法的时间复杂度为 O(m+n)，其中 m 是模式串长度，n 是文本串长度。预处理模式串的时间复杂度为 O(m)，匹配过程的时间复杂度为 O(n)。

#### 2.1.3 Boyer-Moore算法

Boyer-Moore算法是一种基于模式串坏字符规则和好后缀规则的字符串匹配算法，它通过跳过不匹配的字符来提高匹配效率。

**算法流程：**

1. 预处理模式串，生成坏字符规则表和好后缀规则表。
2. 初始化模式串长度 `m` 和文本串长度 `n`。
3. 初始化模式串匹配位置 `j` 为 `m-1`。
4. 对于文本串中每个字符 `i`（从 `m-1` 到 `n-1`）：
- 如果文本串第 `i` 个字符与模式串第 `j` 个字符匹配，则将 `j` 减 1。
- 如果文本串第 `i` 个字符与模式串第 `j` 个字符不匹配：
- 如果文本串第 `i` 个字符在坏字符规则表中，则将 `j` 更新为坏字符规则表中对应的位置。
- 如果文本串第 `i` 个字符不在坏字符规则表中，则将 `j` 更新为好后缀规则表中对应的位置。
5. 如果 `j` 等于 0，则匹配成功，返回 `i-m+1`。
6. 如果遍历完文本串，则没有匹配项，返回 -1。

**代码实现：**

def boyer_moore_string_matching(text, pattern):
    """
    Boyer-Moore字符串匹配算法

    Args:
        text (str): 文本串
        pattern (str): 模式串

    Returns:
        int: 匹配位置（从 0 开始），如果没有匹配项则返回 -1
    """
    m = len(pattern)
    n = len(text)

    # 预处理模式串，生成坏字符规则表和好后缀规则表
    bad_char_table, good_suffix_table = prepr