树形结构算法：理解树形结构，高效处理层次数据（附算法性能分析）

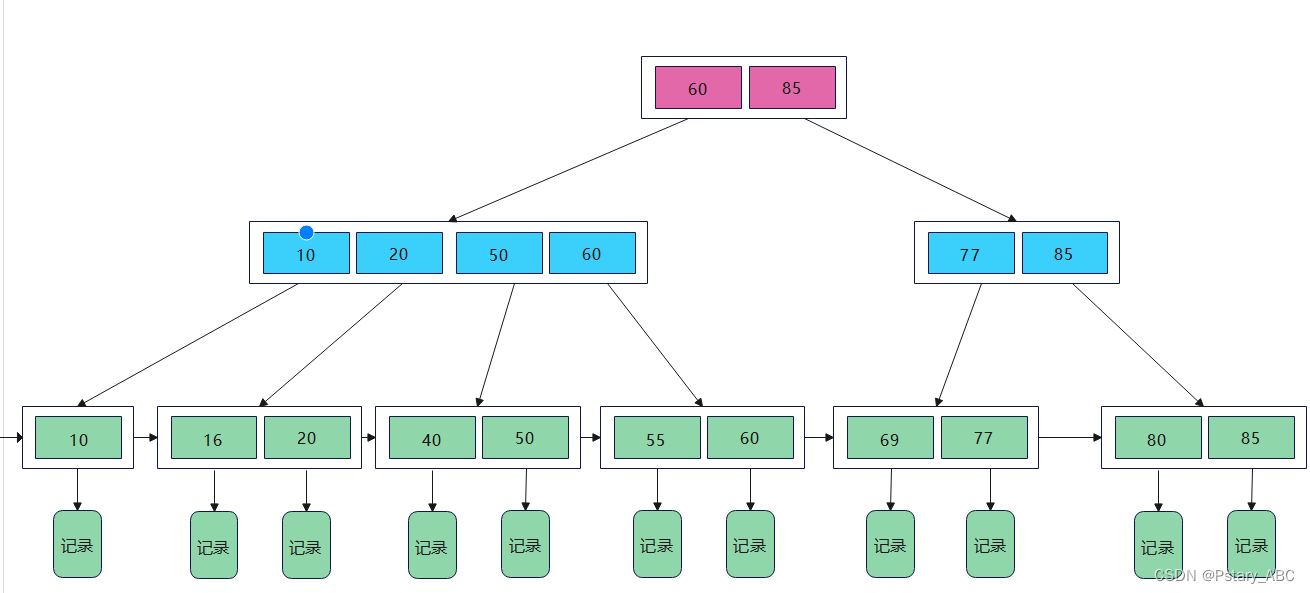
# 1. 树形结构基础**

树形结构是一种非线性数据结构，它具有以下特点：

- 每个节点最多只有一个父节点。
- 每个节点可以有多个子节点。
- 除了根节点外，每个节点都有一个唯一的父节点。

树形结构可以用来表示具有层次关系的数据，例如文件系统、数据库索引和组织结构图。

# 2. 树形结构算法**

**2.1 树的遍历算法**

树的遍历算法是一种系统地访问树中所有节点的方法。有两种主要的遍历算法：深度优先遍历和广度优先遍历。

**2.1.1 深度优先遍历**

深度优先遍历（DFS）从树的根节点开始，并沿着一条路径一直向下遍历，直到到达叶节点。然后，它会回溯到最近未访问过的节点，并继续沿着另一条路径向下遍历。

**代码块：**

def dfs(node):
    """
    深度优先遍历树
    参数：
        node：当前节点
    """
    if node is None:
        return

    # 访问当前节点
    print(node.data)

    # 递归遍历左子树
    dfs(node.left)

    # 递归遍历右子树
    dfs(node.right)

**逻辑分析：**

该代码块实现了深度优先遍历算法。它从当前节点开始，访问该节点，然后递归地遍历左子树和右子树。

**2.1.2 广度优先遍历**

广度优先遍历（BFS）从树的根节点开始，并按层级访问所有节点。它首先访问根节点，然后访问根节点的所有子节点，再访问子节点的所有子节点，依此类推。

**代码块：**

def bfs(node):
    """
    广度优先遍历树
    参数：
        node：当前节点
    """
    if node is None:
        return

    # 创建一个队列，并把根节点入队
    queue = [node]

    # 循环遍历队列
    while queue:
        # 取出队列中的第一个节点
        node = queue.pop(0)

        # 访问当前节点
        print(node.data)

        # 把当前节点的子节点入队
        if node.left:
            queue.append(node.left)
        if node.right:
            queue.append(node.right)

**逻辑分析：**

该代码块实现了广度优先遍历算法。它使用一个队列来存储要访问的节点。它从根节点开始，并把根节点入队。然后，它循环遍历队列，访问队列中的第一个节点，并把该节点的子节点入队。

**2.2 树的搜索算法**

树的搜索算法是一种在树中查找特定节点的方法。有两种主要的搜索算法：二叉查找树的查找算法和平衡树的插入和删除算法。

**2.2.1 二叉查找树的查找算法**

二叉查找树（BST）是一种特殊的二叉树，其中每个节点的值都比其左子树中的所有值大，比其右子树中的所有值小。这使得在 BST 中查找特定值非常高效。

**代码块：**

def search_bst(node, value):
    """
    在二叉查找树中查找特定值
    参数：
        node：当前节点
        value：要查找的值
    返回：
        如果找到，返回节点；否则返回 None
    """
    if node is None:
        return None

    if node.data == value:
        return node

    if value < node.data:
        r