图像识别算法的多尺度处理技巧

# 1. 图像识别算法概述

在现代信息技术飞速发展的今天，图像识别技术已经广泛应用于人工智能、安防监控、医疗诊断、自动驾驶等多个领域。图像识别的核心任务是从图像中提取有价值的信息，完成诸如目标检测、图像分类、特征匹配等任务。

图像识别算法的发展历程伴随着从手工特征提取到深度学习的演进。早期算法依赖于专家精心设计的特征描述符，如SIFT、HOG等，但它们在面对复杂场景时表现往往不尽如人意。随着计算能力的提高和大数据的普及，以卷积神经网络（CNN）为代表的深度学习方法凭借其出色的特征学习能力，在图像识别领域取得了革命性的进展。

深度学习的兴起虽然带来了许多成功案例，但也对算法的计算资源提出了更高要求。因此，如何在保持识别精度的同时减少计算负担，成为研究人员关注的热点。多尺度处理技术，作为实现这一目标的重要手段，通过在不同的尺度空间处理图像信息，有效提升了图像识别的准确率和鲁棒性。在后续章节中，我们将深入探讨多尺度处理的理论基础及其在图像识别领域的应用实践。

# 2. 多尺度处理的基础理论

## 2.1 多尺度表示的数学基础

### 2.1.1 尺度空间理论

尺度空间理论是多尺度图像处理的核心数学基础之一，它提供了一种系统地分析图像在不同尺度下的特性的方式。尺度空间的概念最早由Iijima提出，而后由Witkin、Lindeberg等人进一步发展。在图像处理中，尺度空间理论主要用于定义和构造图像的不同尺度的表示，以便在这些表示上进行特征提取和分析。

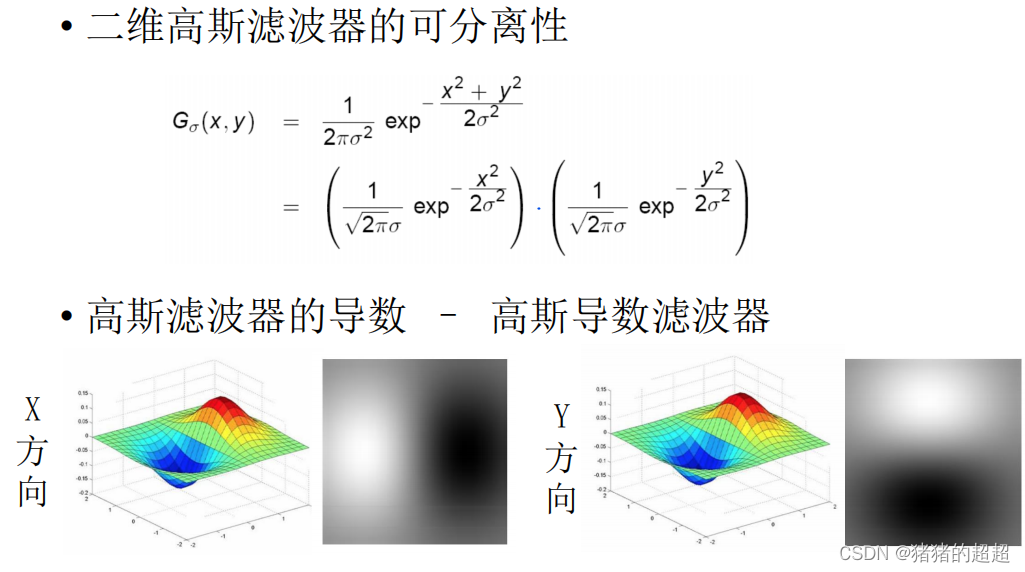
尺度空间表示通常通过在图像的每个像素位置上应用一个线性尺度空间核函数来获得。一个常见的尺度空间核是高斯核，而尺度空间表示可以通过将图像与不同尺度的高斯核进行卷积来构建。对于一个图像函数 \( I(x,y) \)，其在尺度 \( \sigma \) 下的尺度空间表示 \( L(x,y,\sigma) \) 可以表示为：

\[ L(x,y,\sigma) = G(x,y,\sigma) * I(x,y) \]

其中，\( G(x,y,\sigma) \) 是尺度为 \( \sigma \) 的二维高斯函数，\( * \) 表示卷积运算。

在高维尺度空间中，图像可以通过一个由高斯核生成的多尺度核函数来观察，这种表示捕捉了从粗到细的图像结构。因此，尺度空间理论为多尺度图像分析提供了一个坚实的数学框架。

### 2.1.2 小波变换与多分辨率分析

小波变换是一种多分辨率分析方法，它可以对信号进行时间和频率的局部化分析。在图像处理中，小波变换用于多尺度分解，能够有效地提取图像的局部特征，并保持对图像全局特征的理解。

小波变换通过使用一组函数，称为小波基，来分析信号。这些小波基是通过平移和缩放一个母小波函数获得的。对于二维图像，离散小波变换（DWT）会生成多个子带图像，每个子带都对应于不同的空间频率和方向。这些子带图像可以视为图像在不同尺度和方向上的表示。

小波变换的多分辨率特性允许我们从粗略到精细地分析图像内容，类似于在尺度空间理论中使用高斯核的方法。然而，与尺度空间理论不同的是，小波变换能够提供空间频率上的详细信息，这对于多尺度特征的精细分析尤为重要。

多尺度处理的基础理论为图像识别算法提供了必要的数学工具和理论支持。接下来，我们将探讨这些理论在图像识别中的实际应用。

## 2.2 多尺度分析在图像识别中的作用

### 2.2.1 特征提取中的多尺度策略

在图像识别中，特征提取是将原始图像转换为可用于分类或检测的有意义的信息的过程。多尺度策略在特征提取中的应用可以显著提高算法的性能，尤其是在处理具有复杂结构的图像时。

多尺度特征提取通常涉及在不同尺度空间上提取特征，并将这些特征组合起来形成一个完整的特征向量。通过在多个尺度上分析图像，可以同时捕捉到图像的粗略和精细特征，这对于提高识别算法的鲁棒性至关重要。

例如，SIFT（尺度不变特征变换）算法是一种广泛使用的特征提取方法，它在多个尺度上检测关键点，并为每个关键点提取一个包含方向和尺度信息的描述子。SIFT特征具有尺度不变性和旋转不变性，使其在许多图像识别任务中都非常有用。

### 2.2.2 对抗噪声和光照变化的优势

多尺度分析在图像识别中的另一个重要作用是提供对噪声和光照变化的鲁棒性。在现实世界中，图像经常受到噪声和光照变化的影响，这可能会干扰图像识别算法的准确性。

使用多尺度分析，可以在图像的不同尺度级别上考虑这些变化，并通过分析不同尺度下的特征来缓解这些问题。由于噪声和光照变化的影响通常在较小的尺度上更为显著，而更粗糙的尺度则对这些变化不敏感，因此，结合多个尺度的特征可以提高算法的鲁棒性。

例如，在进行面部识别时，如果只使用单一尺度的特征，面部的一些关键部分可能会因为光照的局部变化而变得难以辨认。然而，通过在多尺度上分析面部图像，算法可以利用不同尺度上稳定存在的特征，从而提高识别的准确性。

多尺度处理的基础理论为我们理解和应用多尺度图像识别技术奠定了基础。下一章将介绍多尺度处理技术的实践应用。

# 3. 多尺度处理技术的实践应用

多尺度处理技术广泛应用于图像识别领域，它能够通过不同的尺度变化来处理图像，增强特征的表达能力。本章节将从实际的技术应用出发，深入讨论多尺度处理技术在构建尺度空间与特征检测、多尺度融合技术，以及在实际应用案例中的运用。

## 3.1 尺度空间的构建与特征检测

尺度空间是多尺度图像处理的基础，它能够表征图像特征在不同尺度下的变化。尺度空间的构建对于特征检测算法至关重要。

### 3.1.1 高斯金字塔与特征尺度选择

高斯金字塔是一种多尺度图像表示方法，通过低通滤波和降采样实现图像的多尺度分解。高斯金字塔在多尺度特征提取中占据重要地位，因为它能够在不同的尺度上保持图像的结构信息。

import cv2
import numpy as np

# 构建高斯金字塔
def build_gaussian_pyramid(image, levels):
    pyramid = [image]
    for i in range(levels):
        image = cv2.pyrDown(image)
        pyramid.append(image)
    return pyramid

# 假设有一个输入图像
input_image = cv2.imread('input_image.jpg')
levels = 4
gaussian_pyramid = build_gaussian_pyramid(