揭秘NP完全问题：算法复杂度中的终极难题

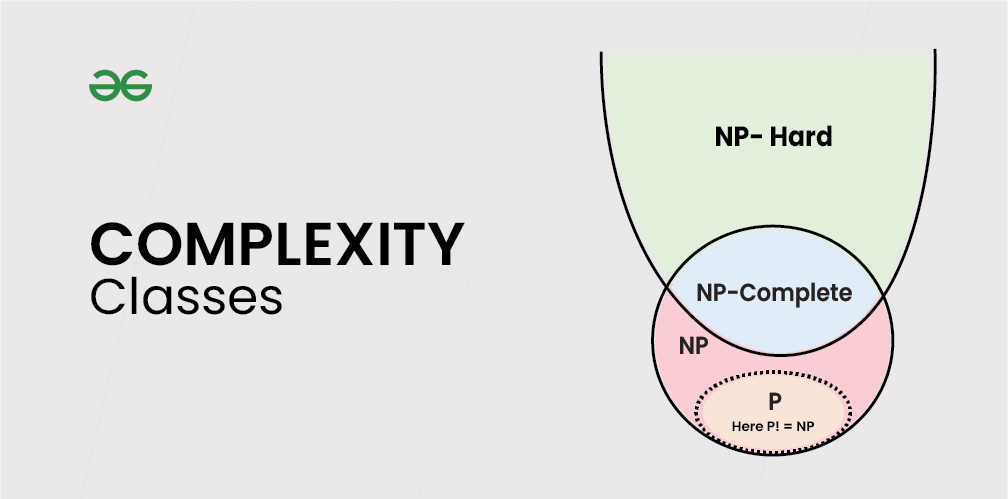
# 1. NP完全问题的定义与性质

**1.1 定义**

NP完全问题是指在多项式时间内可以验证解的正确性，但不能在多项式时间内找到解的一类问题。换句话说，对于NP完全问题，我们可以快速检查一个给定的解是否正确，但找到一个正确的解却非常困难。

**1.2 性质**

NP完全问题具有以下性质：

- **多项式时间可验证：**对于任何给定的解，都可以使用多项式时间算法验证其正确性。
- **多项式时间归约：**任何NP问题都可以通过多项式时间归约转化为NP完全问题。
- **NP-hard：**NP完全问题至少与所有NP问题一样难。
- **NP-complete：**NP完全问题既是NP问题，又是NP-hard问题。

# 2. NP完全问题的求解方法

NP完全问题是计算机科学中一类重要的优化问题，由于其计算复杂度极高，目前尚无高效的算法能够在多项式时间内求解。因此，针对NP完全问题的求解，研究人员提出了多种近似求解方法。

### 2.1 暴力穷举法

#### 2.1.1 基本原理

暴力穷举法是一种最直接的求解NP完全问题的方法，其基本原理是枚举问题的所有可能解，并逐一计算每个解的代价，最终选择代价最小的解作为问题的近似解。

#### 2.1.2 优化策略

暴力穷举法虽然简单易懂，但其计算复杂度极高，随着问题规模的增大，其求解时间将呈指数级增长。为了提高暴力穷举法的效率，可以采用以下优化策略：

- **剪枝策略：**在枚举过程中，如果发现某个解的代价已经超过了当前已知最优解的代价，则可以剪枝，不再枚举该解的后继解。
- **启发式策略：**在枚举过程中，可以根据问题的特点，采用一些启发式规则来指导枚举顺序，从而优先枚举可能包含最优解的解空间。

### 2.2 近似算法

近似算法是一种针对NP完全问题的近似求解方法，其目标是找到一个解，使得该解的代价与最优解的代价之差在一定范围内。近似算法的计算复杂度通常较低，并且能够在多项式时间内求解问题。

#### 2.2.1 贪心算法

贪心算法是一种近似算法，其基本原理是每次从当前可行的解中选择一个局部最优解，并将其加入到最终解中。贪心算法的计算复杂度通常较低，但其求解质量可能受到局部最优解的影响。

#### 2.2.2 局部搜索算法

局部搜索算法是一种近似算法，其基本原理是在当前解的基础上，通过局部扰动的方式生成新的解，并不断迭代，直至找到一个局部最优解。局部搜索算法的计算复杂度通常较高，但其求解质量往往优于贪心算法。

#### 2.2.3 遗传算法

遗传算法是一种近似算法，其基本原理是模拟生物的进化过程，通过选择、交叉和变异等操作，不断生成新的解，并选择适应度最高的解作为问题的近似解。遗传算法的计算复杂度通常较高，但其求解质量往往优于贪心算法和局部搜索算法。

### 2.2.4 比较

下表比较了暴力穷举法、贪心算法、局部搜索算法和遗传算法的优缺点：

| 算法 | 优点 | 缺点 |
|---|---|---|
| 暴力穷举法 | 能够找到最优解 | 计算复杂度极高 |
| 贪心算法 | 计算复杂度低 | 求解质量受局部最优解影响 |
| 局部搜索算法 | 求解质量优于贪心算法 | 计算复杂度较高 |
| 遗传算法 | 求解质量优于贪心算法和局部搜索算法 | 计算复杂度最高 |

# 3. NP完全问题的实际应用

NP完全问题在实际应用中具有广泛的应用，尤其是在组合优化和图论领域。

### 3.1 组合优化问题

组合优化问题是指在有限的可行解集合中找到一个最优解的问题。NP完全问题在组合优化问题中有着广泛的应用，其中最具代表性的两个问题是旅行商问题和背包问题。

#### 3.1.1 旅行商问题

旅行商问题是一个经典的NP完全问题，描述如下：给定一个城市列表和城市之间的距离，找到一条最短的路径，访问所有城市并返回起点。

旅行商问题在现实世界中有着广泛的应用，例如：

- 物流和运输：优化车辆路线以减少配送成本。
- 制造业：优化生产线顺序以提高效率。
- 旅游业：规划最优的旅游路线以节省时间和成本。

#### 3.1.2 背包问题

背包问题是一个NP完全问题，描述如下：给定一个背包容量和一系列物品，每个物品都有其重量和价值，在不超过背包容量的情况下，选择一个物品集合，使总价值最大化。

背包问题在现实世界中也有着广泛的应用，例如：

- 资源分配：在有限的预算下，优化资源分配以获得最大的收益。
- 项目选择：从一系列项目中选择一个项目组合，以最大化总收益或最小化总成本。
- 库存管理：优化库存水平以满足需求，同时最大化利润。

### 3.2 图论问题

图论问题是与图相关的数学问题。NP完全问题在图论问题中也有着广泛的应用，其中最具代表性的两个问题是最小生成树问题和最大匹配问题。

#### 3.2.1 最小生成树问题

最小生成树问题是一个NP完全问题，描述如下：给定一个加权无向图，找到一个生成树，使总权重最小。

最小生成树问题在现实世界中有着广泛的应用，例如：

- 网络设计：设计一个网络，以最小的成本连接所有节点。
- 电路设计：设计一个电路，以最小的电阻连接所有组件。
- 数据传输：优化数据传输网络，以最小的带宽连接所有节点。

#### 3.2.2 最大匹配问题

最大匹配问题是一个NP完全问题，描述如下：给定一个二分图，找到一个匹配，使匹配的边数最大。

最大匹配问题在现实世界中有着广泛的应用，例如：

- 分配问题：将一组任务分配给一组人员，以最大化匹配度。
- 稳定婚姻问题：将一组男性和女性配对，以最大化匹配的稳定性。
- 资源分配：在有限的资源下，优化资源分配以最大化匹配度。

# 4. NP完全问题的理论研究

### 4.1 NP完全性的证明

NP完全性的证明是NP完全问题理论研究的核心内容。目前，主要有两种证明方法：归约法和对角线论证法。

**4.1.1 归约法**

归约法是证明一个问题NP完全性的最常用方法。其基本思想是将一个已知NP完全的问题（称为源问题）归约到待证明的问题（称为目标问题）。如果目标问题可以通过多项式时间算法从源问题推导出来，则目标问题也是NP完全的。

**归约法的步骤：**

1. 选择一个已知的NP完全问题作为源问题。
2. 设计一个多项式时间算法，将源问题实例转换为目标问题实例。
3. 证明转换后的目标问题实例与源问题实例具有相同的结果。

**例如：**证明旅行商问题（TSP）是NP完全的。

* **源问题：**哈密顿回路问题（HCP）
* **归约算法：**给定一个HCP实例（一个带权图G），构造一个TSP实例（一个带权图G'），其中G'的权重与G的权重相同，并且G'中存在一条哈密顿回路当且仅当G中存在一条哈密顿回路。
* **证明：**转换后的TSP实例与HCP实例具有相同的结果，因为TSP中找到最短哈密顿回路等价于HCP中找到哈密顿回路。

**4.1.2 对角线论证法**

对角线论证法是一种间接证明方法，用于证明一个问题NP完全的。其基本思想是构造一个NP完全问题集合，并证明待证明的问题属于该集合。

**对角线论证法的步骤：**

1. 定义一个NP完全问题集合C。
2. 构造一个问题P，其输入是一个图灵机M和一个输入字符串x。
3. 证明P属于集合C。
4. 证明如果P不是NP完全的，则C中存在一个问题不是NP完全的。

**例如：**证明SAT问题（求解布尔可满足性问题）是NP完全的。

* **集合C：**所有NP完全问题
* **问题P：**给定一个图灵机M和一个输入字符串x，确定M在x上的运行是否会停止。
* **证明：**P属于集合C，因为P可以归约到HCP。如果P不是NP完全的，则C中存在一个问题不是NP完全的，这与C的定义矛盾。

### 4.2 NP难问题的性质

NP难问题是指至少与某个NP完全问题一样难的问题。NP难问题具有以下性质：

**4.2.1 NP-hard问题**

NP-hard问题是至少与某个NP完全问题一样难的问题。换句话说，如果存在一个多项式时间算法可以解决某个NP-hard问题，则所有NP完全问题都可以通过多项式时间算法解决。

**4.2.2 NP-complete问题**

NP-complete问题是NP-hard问题，且本身也是NP问题。换句话说，NP-complete问题是NP问题中最难的问题。

**NP-hard问题和NP-complete问题的区别：**

* NP-hard问题可能不是NP问题，而NP-complete问题一定是NP问题。
* NP-complete问题比NP-hard问题更难，因为它们不仅难解，而且是NP问题中最难解的。

# 5. NP完全问题的挑战与展望

### 5.1 量子计算对NP完全问题的潜在影响

量子计算的兴起为解决NP完全问题带来了新的希望。量子计算机利用量子力学的叠加和纠缠特性，可以并行处理大量可能的状态，从而大幅提升计算效率。

对于某些NP完全问题，量子算法已被证明具有指数级的加速效果。例如，Shor算法可以高效分解大整数，这对于基于整数分解的密码算法（如RSA）构成了重大威胁。

然而，量子计算目前仍处于早期发展阶段，其稳定性和可扩展性还有待提高。此外，量子算法的实现需要专门的硬件和软件支持，这增加了其应用的难度。

### 5.2 新算法和技术的探索

除了量子计算，研究人员也在不断探索新的算法和技术来解决NP完全问题。这些方法包括：

* **近似算法的改进：**近似算法可以提供问题的近似解，虽然不能保证最优解，但可以大幅降低计算复杂度。研究人员正在开发新的近似算法，以提高其近似质量和效率。
* **启发式算法：**启发式算法是一种基于经验和直觉的算法，不保证最优解，但往往可以在实际应用中获得较好的效果。近年来，蚁群算法、粒子群算法等启发式算法在解决NP完全问题方面取得了显著进展。
* **并行算法：**并行算法利用多核处理器或分布式计算来同时处理多个子问题，从而提高计算效率。研究人员正在开发新的并行算法，以充分利用现代计算机的并行能力。

### 5.3 NP完全问题的应用拓展

随着计算技术的不断发展，NP完全问题在各领域的应用范围也在不断拓展。除了传统应用领域（如组合优化、图论），NP完全问题还被应用于：

* **人工智能：**NP完全问题在人工智能中扮演着重要角色，例如在机器学习中用于模型选择和超参数优化。
* **大数据分析：**NP完全问题可用于处理海量数据，例如在数据挖掘中用于模式识别和异常检测。
* **金融建模：**NP完全问题在金融建模中用于优化投资组合和风险管理。

NP完全问题的广泛应用表明，解决这些问题的挑战和机遇并存。通过不断探索新的算法和技术，以及拓展其应用领域，NP完全问题将继续在科学、工程和商业等领域发挥重要作用。

# 6. NP完全问题在其他领域的应用

### 6.1 密码学

NP完全问题在密码学中有着广泛的应用，特别是在设计和破解密码算法方面。

**应用场景：**

* **密钥生成：**NP完全问题可用于生成难以破解的加密密钥。例如，基于素数分解的RSA算法利用了大整数分解的NP完全性。
* **密码分析：**NP完全问题可用于破解密码。例如，基于子集和问题的密码分析技术可以破解某些类型的加密算法。

**优化策略：**

* **启发式算法：**由于NP完全问题通常难以直接求解，因此可以使用启发式算法来寻找近似解。例如，遗传算法可用于优化密钥生成和密码分析过程。
* **并行计算：**利用并行计算技术可以加速NP完全问题的求解。例如，通过分布式计算，可以并行搜索密钥空间或破解密码。

### 6.2 生物信息学

NP完全问题在生物信息学中也得到了应用，特别是在基因组分析和序列比对方面。

**应用场景：**

* **基因组组装：**NP完全问题可用于将来自不同来源的DNA片段组装成完整的基因组。例如，贪心算法可用于优化片段重叠和对齐过程。
* **序列比对：**NP完全问题可用于比较不同的生物序列，以识别相似性或差异性。例如，基于动态规划的算法可用于优化序列比对过程。

**优化策略：**

* **启发式算法：**启发式算法可用于寻找近似解，从而提高基因组组装和序列比对的效率。例如，局部搜索算法可用于优化片段对齐和序列比对过程。
* **并行计算：**并行计算可用于加速生物信息学中NP完全问题的求解。例如，通过云计算，可以并行执行基因组组装和序列比对任务。

### 6.3 经济学

NP完全问题在经济学中也有应用，特别是在优化资源分配和决策制定方面。

**应用场景：**

* **资源分配：**NP完全问题可用于优化资源分配，例如在供应链管理和生产计划中。例如，基于整数规划的算法可用于优化资源分配和调度过程。
* **决策制定：**NP完全问题可用于辅助决策制定，例如在投资组合优化和风险管理中。例如，基于分支定界法的算法可用于优化投资组合选择和风险管理策略。

**优化策略：**

* **启发式算法：**启发式算法可用于寻找近似解，从而提高经济学中NP完全问题的求解效率。例如，贪心算法可用于优化资源分配和决策制定过程。
* **并行计算：**并行计算可用于加速经济学中NP完全问题的求解。例如，通过分布式计算，可以并行执行资源分配和决策制定任务。