NP完全问题实战指南：破解组合优化难题的利器

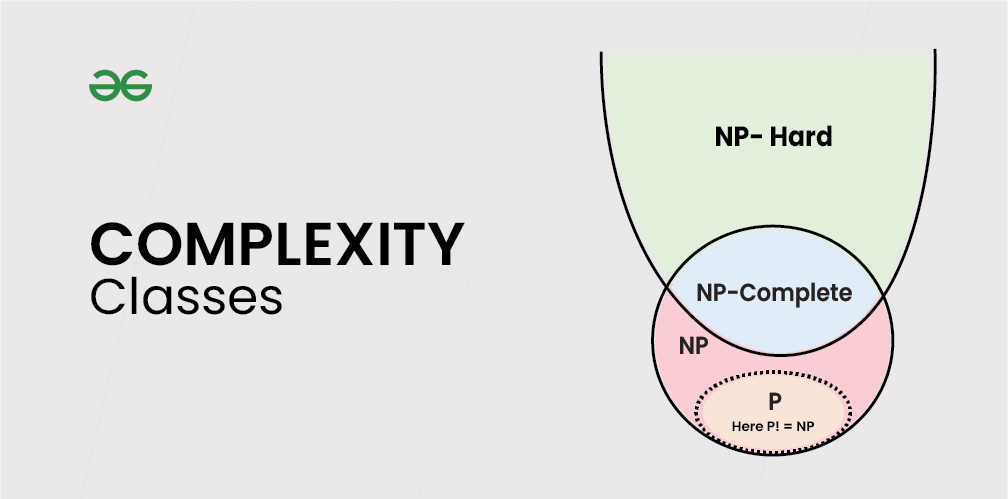
# 1. NP完全问题概述**

NP完全问题是计算机科学中一类特殊的优化问题，它们具有以下特点：

* **非确定性多项式时间 (NP)：**可以在多项式时间内验证给定的解决方案是否正确。
* **完全性：**任何其他NP问题都可以通过多项式时间归约转换为该问题。

NP完全问题之所以重要，是因为它们代表了一类难以求解的优化问题。如果一个问题是NP完全的，则意味着不可能在合理的时间内找到最优解。因此，对于NP完全问题，研究人员通常会采用近似算法或启发式算法来寻找近似最优解。

# 2. NP完全问题求解理论

### 2.1 复杂性理论基础

**复杂性理论**研究计算问题的难度，将问题分为不同的复杂度类。最常见的复杂度类是：

* **P (多项式时间)：**可以在多项式时间内解决的问题。
* **NP (非确定性多项式时间)：**可以在非确定性多项式时间内验证解决方案的问题。

**非确定性**是指问题存在一个“猜测”机制，允许算法对某些输入做出猜测，然后验证猜测的正确性。

### 2.2 NP完全性的定义和性质

**NP完全问题**是NP问题中的一类特殊问题，具有以下性质：

* **NP：**属于NP问题，即可以在非确定性多项式时间内验证解决方案。
* **完全：**任何NP问题都可以归约到该问题。

归约是指将一个问题转化为另一个问题，使得后者的解决方案可以解决前者的解决方案。

### 2.3 NP完全问题的分类和典型案例

NP完全问题可以分为以下几类：

* **组合优化问题：**寻找最优解的问题，如旅行商问题、背包问题。
* **逻辑问题：**确定命题公式是否可满足的问题，如布尔可满足性问题。
* **图论问题：**涉及图结构的问题，如顶点覆盖问题、团问题。

**典型案例：**

* **旅行商问题：**给定一组城市和两城市之间的距离，找到一条访问所有城市并返回起点的最短路径。
* **背包问题：**给定一组物品及其重量和价值，在背包容量限制下，选择物品组合以获得最大价值。
* **布尔可满足性问题：**给定一个布尔公式，确定是否存在一组真值分配使得公式为真。

**代码块：**

def is_satisfiable(formula):
    """
    检查布尔公式是否可满足。

    参数：
        formula (str): 布尔公式，由逻辑运算符和变量组成。

    返回：
        bool: True 如果公式可满足，False 否则。
    """

    # 将公式转换为 CNF 形式
    cnf_formula = convert_to_cnf(formula)

    # 使用回溯法搜索满足赋值
    return backtrack(cnf_formula, {})

def backtrack(formula, assignment):
    """
    使用回溯法搜索满足赋值。

    参数：
        formula (dict): CNF 形式的布尔公式。
        assignment (dict): 当前变量赋值。

    返回：
        bool: True 如果找到满足赋值，False 否则。
    """

    # 如果公式为空，则找到了满足赋值
    if not formula:
        return True

    # 选择一个未赋值的变量
    variable = next(iter(set(formula) - set(assignment)))

    # 尝试为变量赋值为 True
    if backtrack(formula - {variable: True}, assignment | {variable: True}):
        return True

    # 尝试为变量赋值为 False
    if backtrack(formula - {variable: False}, assignment | {variable: False}):
        return True

    # 两种赋值都失败，返回 False
    return False

**逻辑分析：**

`is_satisfiable()` 函数首先将公式转换为 CNF 形式，然后使用回溯法搜索满足赋值。回溯法从一个空赋值开始，逐个变量地进行赋值，并检查是否满足公式。如果找到满足赋值，则返回 `True`；否则，返回 `False`。

**参数说明：**

* `formula`：要检查的布尔公式。
* `assignment`：当前变量赋值。

**mermaid流程图：**

graph LR
subgraph Backtrack
    start[开始] --> check_formula[检查公式]
    check_formula --> assign_variable[赋值变量]
    assign_variable --> backtrack_true[回溯赋值为 True]
    backtrack_true --> check_formula
    assign_variable --> backtrack_false[回溯赋值为 False]
    backtrack_false --> check_formula
    check_formula --> found_solution[找到解决方案]
    check_formula --> no_solution[没有解决方案]
end

# 3. NP完全问题求解实践**

### 3.1 贪心算法和启发式算法

#### 贪心算法

贪心算法是一种基于局部最优选择策略的算法，其主要思想是：在每个决策点上，选择当前看来最优的选项，而无需考虑其对未来决策的影响。贪心算法简单易懂，计算效率较高，但其缺点是不能保证得到全局最优解。

**例子：**

* **背包问题：**在背包容量有限的情况下，选择价值最高的物品装入背包，直到背包装满。

**代码块：**

def greedy_knapsack(items, capacity):
    """
    贪心算法求解背包问题

    Args:
        items: 物品列表，每个物品包含价值和重量
        capacity: 背包容量

    Returns:
        装入背包的物品列表
    """

    # 按价值密度（价值/重量）降序排列物品
    items.sort(key=lambda item: item.value / item.weight, reverse=True)

    # 初始化背包
    backpack = []
    total_value = 0
    total_weight = 0

    # 遍历物品列表
    for item in items:
        # 如果物品重量不超过剩余容量
        if item.weight <= capacity - total_weight:
            # 将物品装入背包
            backpack.append(item)
            total_value += item.value
            total_weight += item.weight

    return backpack

**逻辑分析：**

该代码块实现了背包问题的贪心算法。首先，将物品按价值密度降序排列，然后依次遍历物品列表，将重量不超过剩余容量的物品装入背包。该算法的复杂度为 O(n log n)，其中 n 为物品数量。

#### 启发式算法

启发式算法是一种基于经验和直觉的算法，其主要思想是：利用某些启发式规则来指导搜索过程，以提高找到较优解的概率。启发式算法不能保证得到最优解，但其往往能够在较短时间内得到较好的解。

**例子：**

* **模拟退火：**模拟金属退火过程，通过逐渐降低温度来搜索解空间，以提高找到全局最优解的概率。
* **遗传算法：**模拟生物进化过程，通过选择、交叉和变异等操作来优化解。

**代码块：**

import random

def simulated_annealing(problem, initial_temperature, cooling_rate):
    """
    模拟退火算法求解问题

    Args:
        problem: 问题实例
        initial_temperature: 初始温度
        cooling_rate: 降温速率

    Returns:
        最优解
    """

    # 初始化当前解和最优解
    current_solution = problem.random_solution()
    best_solution = current_solution

    # 循环退火过程
    while initial_temperature > 0:
        # 产生邻域解
        neighbor_solution = problem.neighbor(current_solution)

        # 计算邻域解的能量差
        delta_energy = neighbor_solution.energy() - current_solution.energy()

        # 如果邻域解的能量更低，则接受该解
        if delta_energy < 0 or random.random() < math.exp(-delta_energy / initial_temperature):
            current_solution = neighbor_solution

        # 如果邻域解的能量更高，则以一定概率接受该解
        else:
            current_solution = neighbor_solution

        # 更新最优解
        if current_solution.energy() < best_solution.energy():
            best_solution = current_solution

        # 降低温度
        initial_temperature *= cooling_rate

    return best_solution

**逻辑分析：**

该代码块实现了模拟退火算法。首先，初始化当前解和最优解。然后，循环退火过程，产生邻域解，计算邻域解的能量差，并根据能量差和当前温度决定是否接受该解。最后，返回最优解。该算法的复杂度取决于问题规模和降温速率。

# 4. NP完全问题应用场景

NP完全问题在现实世界中有着广泛的应用，涵盖了从组合优化到密码学等各个领域。本章将探讨NP完全问题在以下三个方面的应用场景：

### 4.1 组合优化问题

组合优化问题是寻求一组可行解中具有最佳目标函数值的解的问题。NP完全问题在组合优化领域有着重要的应用，以下列出一些典型的例子：

#### 4.1.1 旅行商问题

旅行商问题（TSP）是一个经典的NP完全问题，它要求找到一个最短的哈密顿回路，即访问给定城市集中的所有城市并返回到起点。TSP在物流、调度和规划等领域有着广泛的应用。

#### 4.1.2 背包问题

背包问题是一个NP完全问题，它要求在给定的背包容量限制下，从一组物品中选择一个子集，以最大化背包中物品的总价值。背包问题在资源分配、投资组合优化和库存管理等领域有着应用。

#### 4.1.3 排班问题

排班问题是一个NP完全问题，它要求为一组任务分配时间和资源，以满足各种约束条件，例如任务依赖关系、资源可用性和时间限制。排班问题在生产调度、人员调度和项目管理等领域有着应用。

### 4.2 密码学和信息安全

NP完全问题在密码学和信息安全中也扮演着重要的角色。以下是一些例子：

#### 4.2.1 素数分解

素数分解是一个NP完全问题，它要求将一个给定的整数分解成其质因数。素数分解在密码学中用于生成密钥和验证数字签名。

#### 4.2.2 离散对数

离散对数是一个NP完全问题，它要求找到一个整数x，使得g^x = h，其中g和h是给定的整数。离散对数在密码学中用于生成密钥和验证数字签名。

### 4.3 生物信息学和计算化学

NP完全问题在生物信息学和计算化学中也有着应用。以下是一些例子：

#### 4.3.1 DNA序列比对

DNA序列比对是一个NP完全问题，它要求找到两个DNA序列之间的最佳比对，即最大化匹配的碱基对数量。DNA序列比对在基因组学、进化生物学和医学诊断等领域有着应用。

#### 4.3.2 蛋白质折叠

蛋白质折叠是一个NP完全问题，它要求预测一个蛋白质分子的三维结构。蛋白质折叠在药物设计、生物技术和材料科学等领域有着应用。

# 5. NP完全问题研究前沿

### 5.1 量子计算和NP完全问题

近年来，量子计算技术的飞速发展为NP完全问题的求解带来了新的曙光。量子计算机利用量子力学的叠加和纠缠特性，可以并行处理大量数据，从而大幅提升计算效率。对于某些NP完全问题，量子算法已被证明具有指数级的加速能力。

例如，在旅行商问题中，量子算法可以通过叠加态表示所有可能的路径，并利用纠缠操作同时探索这些路径，从而找到最优解。这种方法比经典算法的复杂度降低了指数级。

### 5.2 理论计算机科学和NP完全问题

NP完全问题在理论计算机科学中占据着重要地位。研究者们不断探索NP完全性的本质和边界，寻求新的分类方法和求解技术。

一个活跃的研究方向是NP中间性的问题。NP中间性是指一个问题既不是NP完全的，也不是NP难的。对于NP中间性问题的性质和分布，目前仍存在许多未解之谜。

### 5.3 NP完全问题与人工智能

NP完全问题与人工智能领域有着密切的联系。许多人工智能问题，如规划、调度和博弈，都本质上是NP完全的。

研究者们探索利用人工智能技术，如机器学习和深度学习，来近似求解NP完全问题。通过训练神经网络或强化学习模型，可以获得在特定问题实例上表现良好的近似解。