NP完全问题的实际应用：从理论到现实的跨越

# 1. NP完全问题的理论基础**

NP完全问题是计算机科学中一个重要的概念，它描述了一类具有内在计算复杂性的问题。这些问题即使对于相对较小的输入规模，也需要指数级的时间才能求解。

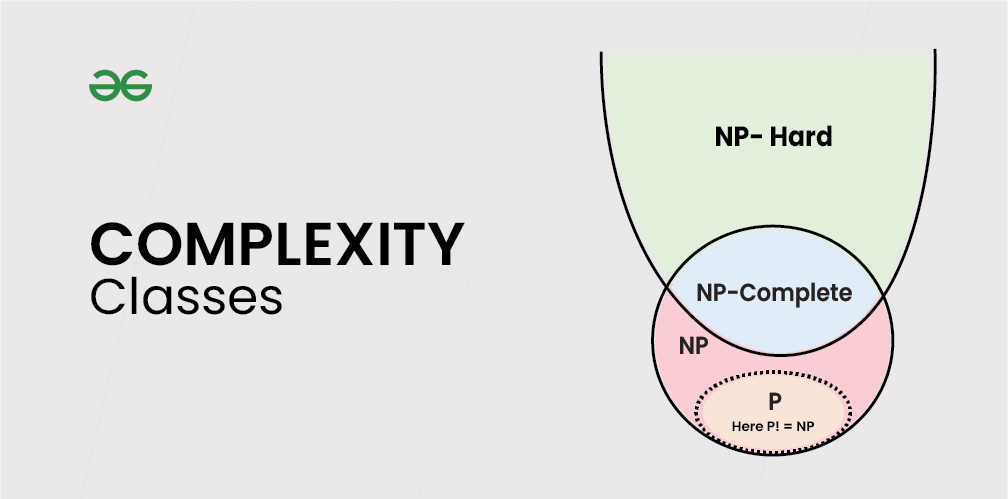
NP完全问题与NP问题密切相关，后者是一类可以在多项式时间内验证其解的问题。然而，对于NP完全问题，即使在已知解的情况下，也无法在多项式时间内找到该解。这种内在的复杂性使得NP完全问题对于许多实际应用来说具有挑战性。

NP完全问题的理论基础建立在计算复杂性理论之上，该理论研究不同问题类型的计算资源需求。通过证明一个问题是NP完全的，我们可以推断它与其他已知的NP完全问题具有同等的计算复杂性。这使得我们能够将解决一个NP完全问题的方法应用到其他类似问题上，从而简化了求解过程。

# 2. NP完全问题的实际应用**

NP完全问题在现实世界中有着广泛的应用，特别是在算法优化和决策支持领域。

**2.1 算法优化：从理论到实践**

NP完全问题在算法优化中扮演着至关重要的角色。通过将复杂问题转化为NP完全问题，我们可以利用现有的算法技术来寻找近似最优解。

**2.1.1 遗传算法的应用**

遗传算法是一种受生物进化启发的优化算法。它通过模拟自然选择过程，在候选解的群体中进行迭代搜索，以寻找最优解。

import random

# 遗传算法伪代码
def genetic_algorithm(population_size, generations, crossover_rate, mutation_rate):
    population = initialize_population(population_size)
    for generation in range(generations):
        # 选择
        parents = select_parents(population)
        # 交叉
        offspring = crossover(parents, crossover_rate)
        # 变异
        offspring = mutate(offspring, mutation_rate)
        # 评估
        population = evaluate(offspring)
    return population[0]  # 返回最优个体

**参数说明：**

* population_size：种群规模
* generations：迭代次数
* crossover_rate：交叉率
* mutation_rate：变异率

**代码逻辑：**

1. 初始化种群，即随机生成一组候选解。
2. 对于每一代，选择种群中的个体作为父母。
3. 对父母进行交叉操作，产生新的后代。
4. 对后代进行变异操作，引入随机性。
5. 评估后代的适应度，并保留最优个体。
6. 重复步骤 2-5，直到达到最大迭代次数。

**2.1.2 模拟退火算法的应用**

模拟退火算法是一种受热力学退火过程启发的优化算法。它通过逐渐降低温度，在候选解的空间中进行搜索，以寻找最优解。

import math

# 模拟退火算法伪代码
def simulated_annealing(initial_temperature, cooling_rate, iterations):
    current_solution = initialize_solution()
    best_solution = current_solution
    temperature = initial_temperature
    for iteration in range(iterations):
        # 产生邻域解
        neighbor = generate_neighbor(current_solution)
        # 计算能量差
        delta_energy = evaluate(neighbor) - evaluate(current_solution)
        # 接受邻域解的概率
        probability = math.exp(-delta_energy / temperature)
        # 根据概率接受或拒绝邻域解
        if random.random() < probability:
            current_solution = neighbor
        # 更新最优解
        if evaluate(current_solution) > evaluate(best_solution):
            best_solution = current_solution
        # 降低温度
        temperature *= cooling_rate
    return best_solution

**参数说明：**

* initial_temperature：初始温度
* cooling_rate：冷却率
* iterations：迭代次数

**代码逻辑：**

1. 初始化解，即随机生成一个候选解。
2. 对于每一代，产生邻域解，即对当前解