NP完全问题与算法复杂度：深入剖析计算极限

# 1. 计算复杂度的基础**

计算复杂度是计算机科学中衡量算法效率的重要指标。它描述了算法在输入规模增长时所需的时间和空间资源。计算复杂度通常用大 O 符号表示，它表示算法在最坏情况下所需资源的渐近增长率。

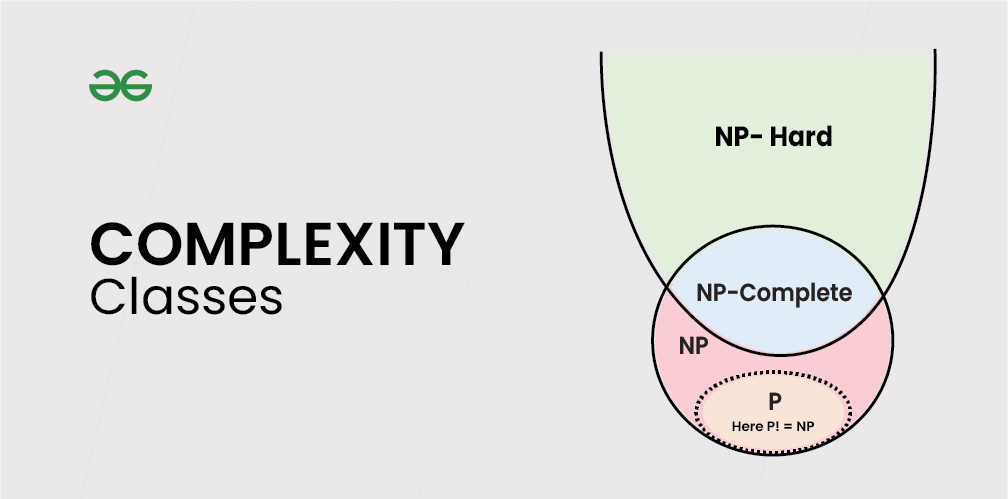
常见的复杂度类包括：

- **多项式时间复杂度（P）：**算法在输入规模 n 的多项式时间内完成，即 O(n^k)，其中 k 是常数。
- **指数时间复杂度（EXP）：**算法在输入规模 n 的指数时间内完成，即 O(2^n)。
- **线性时间复杂度（O(n))：**算法在输入规模 n 的线性时间内完成，即所需时间与输入规模成正比。

# 2. NP完全问题的理论基础

### 2.1 NP问题和NP完全问题的定义

**NP问题：**

* **定义：**NP（非确定性多项式时间）问题是指可以在多项式时间内通过非确定性图灵机解决的问题。
* **特征：**
* 问题可以快速验证解决方案。
* 问题本身难以解决。

**NP完全问题：**

* **定义：**NP完全问题是NP问题中最难的问题，它具有以下特性：
* 属于NP问题。
* 任何NP问题都可以通过多项式时间约简归约到该问题。

### 2.2 NP完全问题的性质和特征

**性质：**

* **多项式时间验证：**NP完全问题可以通过多项式时间算法验证解决方案的正确性。
* **多项式时间归约：**任何NP问题都可以通过多项式时间约简归约到NP完全问题。
* **NP困难：**NP完全问题至少与NP问题一样难。

**特征：**

* **组合优化问题：**NP完全问题通常涉及组合优化问题，例如旅行商问题、背包问题等。
* **搜索空间巨大：**NP完全问题的搜索空间通常非常大，使得暴力穷举法不可行。
* **启发式算法：**解决NP完全问题通常需要使用启发式算法或近似算法。

### 代码示例：

考虑以下旅行商问题：

import numpy as np

def tsp(cities):
  """
  旅行商问题：给定一组城市，求出最短的环路，访问所有城市一次并返回起点。

  参数：
    cities：城市列表，每个城市用其坐标表示。

  返回：
    最短环路的距离。
  """

  # 计算城市之间的距离矩阵
  distances = np.zeros((len(cities), len(cities)))
  for i in range(len(cities)):
    for j in range(len(cities)):
      distances[i, j] = np.linalg.norm(cities[i] - cities[j])

  # 初始化最短距离和路径
  min_distance = float('inf')
  min_path = []

  # 暴力穷举所有可能的环路
  for i in range(len(cities)):
    for j in range(len(cities)):
      if i == j:
        continue

      # 计算环路的距离
      distance = distances[i, j]
      for k in range(len(cities)):
        if k == i or k == j:
          continue
        distance += distances[j, k]

      # 更新最短距离和路径
      if distance < min_distance:
        min_distance = distance
        min_path = [i, j]

  # 返回最短距离
  return min_distance

**代码逻辑分析：**