NP完全问题：从理论到实战，全面解析其本质

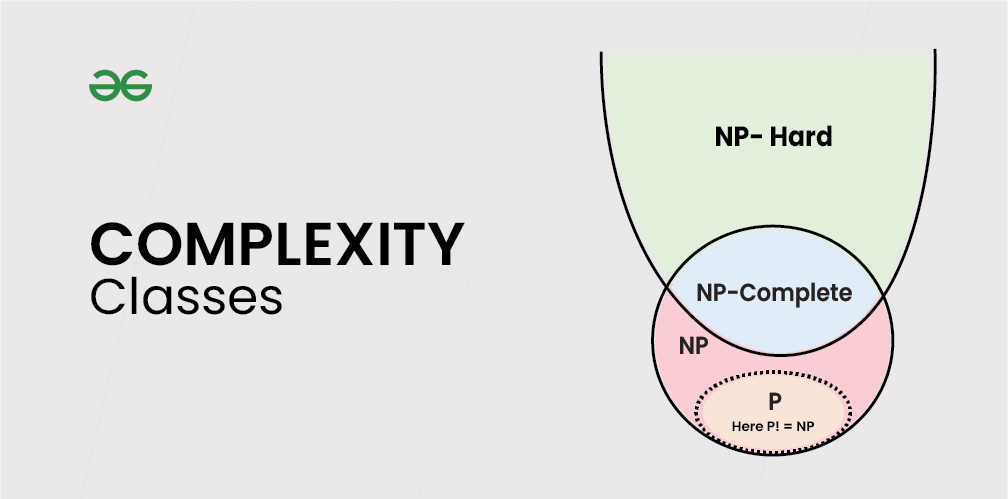
# 1. NP完全问题的理论基础**

NP完全问题是计算机科学中一个重要的概念，它描述了一类具有固有计算难度的优化问题。这些问题具有以下特点：

- **非确定性多项式时间 (NP)**：问题可以在多项式时间内验证，但不能在多项式时间内求解。
- **完全性**：所有其他NP问题都可以多项式时间归约到该问题。

NP完全问题的理论基础建立在图灵机模型和计算复杂性理论之上。图灵机是一种抽象的计算模型，它可以模拟任何算法。计算复杂性理论研究算法的资源消耗，例如时间和空间。通过分析图灵机对NP完全问题的模拟，可以证明这些问题具有固有的计算难度。

# 2. NP完全问题的求解技巧

NP完全问题因其计算复杂性而闻名，求解此类问题需要巧妙的技巧和算法。本章节将深入探讨三种广泛使用的NP完全问题求解技巧：暴力搜索、分支限界法和近似算法。

### 2.1 暴力搜索

暴力搜索是一种朴素而直接的求解方法，它遍历所有可能的解，并选择满足约束条件且目标函数最优的解。对于较小的NP完全问题，暴力搜索可能是一种可行的选择。

**代码块：**

def brute_force(problem):
    """暴力搜索求解NP完全问题。

    参数：
        problem: NP完全问题实例。

    返回：
        最优解。
    """
    best_solution = None
    best_score = float('-inf')

    for solution in problem.generate_all_solutions():
        if problem.is_valid(solution):
            score = problem.evaluate(solution)
            if score > best_score:
                best_solution = solution
                best_score = score

    return best_solution

**逻辑分析：**

* `brute_force` 函数接受一个NP完全问题实例 `problem` 作为参数。
* 它遍历所有可能的解，调用 `problem.generate_all_solutions()` 方法生成解。
* 对于每个解，它检查其有效性（`problem.is_valid()`）并计算其目标函数值（`problem.evaluate()`）。
* 它更新最佳解和最佳分数，直到遍历所有解。
* 最终返回最优解。

### 2.2 分支限界法

分支限界法是一种启发式搜索算法，它通过系统地探索解空间来缩小搜索范围。它维护一个候选解列表，并根据启发式函数对列表进行排序。

**代码块：**

def branch_and_bound(problem):
    """分支限界法求解NP完全问题。

    参数：
        problem: NP完全问题实例。

    返回：
        最优解。
    """
    best_solution = None
    best_score = float('-inf')
    candidates = [problem.initial_solution()]

    while candidates:
        candidate = candidates.pop(0)
        score = problem.evaluate(candidate)
        if score > best_score:
            best_solution = candidate
            best_score = score

        if problem.is_valid(candidate):
            for child in problem.generate_children(candidate):
                candidates.append(child)

    return best_solution

**逻辑分析：**

* `branch_and_bound` 函数接受一个NP完全问题实例 `problem` 作为参数。
* 它从初始解开始，并将其放入候选解列表 `candidates` 中。
* 它从列表中弹出候选解，计算其目标函数值，并更新最佳解和最佳分数。
* 如果候选解有效，它将生成其子解并将其添加到 `candidates` 中。
* 算法重复此过程，直到候选解列表为空。
* 最终返回最优解。

### 2.3 近似算法

近似算法是一种求解NP完全问题的启发式方法，它提供一个目标函数值与最优解值之间的近似保证。近似算法通常比暴力搜索或分支限界法更快，但它们可能不会产生最优解。

**代码块：**

def approximation_algorithm(problem):
    """近似算法求解NP完全问题。

    参数：
        problem: NP完全问题实例。

    返回：
        近似解。
    """
    solution = problem.greedy_solution()
    score = problem.evaluate(solution)
    return solution, score

**逻辑分析：**

* `approximation_algorithm` 函数接受一个NP完全问题实例 `problem` 作为参数。
* 它使用贪婪算法生成一个近似解 `solution`。
* 它计算近似解的目标函数值 `score`。
* 最终返回近似解和目标函数值。

# 3. NP完全问题的实际应用

### 3.1 组合优化问题

组合优化问题是指在给定的约束条件下，从有限的候选解中找到最优解的问题。NP完全问题在组合优化领域有着广泛的应用，包括：

- **旅行商问题 (TSP)**：给定一组城市和两城市之间的距离，找到一条最短的路径，访问所有城市并返回起点。
- **背包问题**：给定一组物品，每个物品有其重量和价值，以及一个背包容量，在不超过背包容量的情况下，找到一个物品集合，其总价值最大。
- **调度问题**：给定一组任务，每个任务有其处理时间和截止时间，在不违反截止时间的情况下，找到一个任务调度，使所有任务都完成。

### 3.2 规划问题

规划问题是指在给定的状态空间中，从初始状态到目标状态找到一条最优路径的问题。NP完全问题在规划领域也有着重要的应用，包括：

- **路径规划**：给定一个地图和起点和终点，找到一条从起点到终点的最短路径，同时避开障碍物。
- **机器人导航**：给定一个机器人和一个环境，找到一条从机器人当前位置到目标位置的最优路径，同时避免碰撞。
- **物流规划**：给定一组货物和一个仓库，找到一个最优的货物运输计划，使所有货物都能及时运送到目的地。

### 3.3 游戏问题

游戏问题是指在给定的游戏规则下，找到一个最优的策略或行动序列的问题。NP完全问题在游戏领域也有着广泛的应用，包括：

- **棋盘游戏**：例如国际象棋和围棋，找到一个最优的走法，以赢得比赛。
- **纸牌游戏**：例如扑克和桥牌，找到一个最优的出牌策略，以获得最大的收益。
- **电子游戏**：例如星际争霸和英雄联盟，找到一个最优的战术或战略，以击败对手。

# 4.1 多项式时间归约

**定义**

多项式时间归约（polynomial-time reduction）是NP完全性证明中至关重要的概念。它是一种将一个问题归约为另一个问题的技术，使得如果归约后的问题是NP完全的，那么原始问题也是NP完全的。

**形式化定义**

问题A多项式时间归约到问题B，记作A ≤_p B，当且仅当存在一个多项式时间算法f，使得对于任何输入x：

* x是A的一个实例
* f(x)是B的一个实例
* x是A的一个解当且仅当f(x)是B的一个解

**证明NP完全性的作用**

多项式时间归约在NP完全性证明中发挥着关键作用。通过将一个已知是NP完全的问题归约到一个新的问题，我们可以证明新问题也是NP完全的。

**具体步骤**

证明问题A是NP完全的步骤如下：

1. 证明A是NP问题。
2. 选择一个已知的NP完全问题B。
3. 构建一个多项式时间算法f，使得对于任何输入x：
* x是A的一个实例
* f(x)是B的一个实例
* x是A的一个解当且仅当f(x)是B的一个解

如果上述步骤都成立，则A是NP完全的。

**示例**

考虑以下问题：

* **问题A：**给定一个集合S和一个整数k，是否存在S的k个元素之和为0？
* **问题B：**给定一个集合S和一个整数k，是否存在S的k个元素之和大于0？

问题B已知是NP完全的。我们可以通过以下多项式时间算法f将问题A归约到问题B：

def f(S, k):
    S' = {-x for x in S}
    return S' + [1] * k

对于任何输入(S, k)，f(S, k)都是一个集合，其元素之和大于0当且仅当S的k个元素之和为0。因此，A ≤_p B，并且A也是NP完全的。

## 4.2 NP完全性的证明

**证明方法**

NP完全性的证明通常遵循以下步骤：

1. 证明问题是NP问题。
2. 将一个已知的NP完全问题归约到该问题。

如果上述步骤都成立，则该问题是NP完全的。

**示例**

考虑以下问题：

* **问题：**给定一个图G和一个整数k，是否存在G的一个k个顶点的团？

我们可以通过将问题“3-SAT”归约到该问题来证明其NP完全性。3-SAT是一个已知的NP完全问题，其定义如下：

* **3-SAT：**给定一个布尔公式，其中每个子句包含3个文字，是否存在一组真值分配，使得该公式为真？

**归约算法**

def f(F):
    G = Graph()
    for clause in F:
        for literal in clause:
            G.add_vertex(literal)
        for i in range(len(clause)):
            for j in range(i + 1, len(clause)):
                G.add_edge(clause[i], clause[j])
    return G, len(F)

对于任何3-SAT公式F，f(F)都是一个图G和一个整数k，使得G中存在一个k个顶点的团当且仅当F可满足。因此，3-SAT ≤_p 团问题，并且团问题也是NP完全的。

## 4.3 NP难问题的判定

**定义**

NP难问题（NP-hard problem）是指至少与某个NP完全问题一样难的问题。

**判定方法**

判定一个问题是否为NP难问题的步骤如下：

1. 选择一个已知的NP完全问题B。
2. 将B归约到该问题。

如果上述步骤成立，则该问题是NP难的。

**示例**

考虑以下问题：

* **问题：**给定一个集合S和一个整数k，是否存在S的k个元素之和为1？

我们可以通过将问题“3-SAT”归约到该问题来证明其NP难性。

**归约算法**

def f(F):
    S = set()
    for clause in F:
        for literal in clause:
            S.add(literal)
    S.add(1)
    return S, len(F)

对于任何3-SAT公式F，f(F)都是一个集合S和一个整数k，使得S的k个元素之和为1当且仅当F可满足。因此，3-SAT ≤_p 1-SUM问题，并且1-SUM问题是NP难的。

# 5. NP完全问题的前沿研究

### 5.1 量子计算在NP完全问题中的应用

量子计算是一种利用量子力学的原理进行计算的新型计算范式。与传统计算机相比，量子计算机具有并行性和叠加性等特性，这使其在求解某些复杂问题上具有潜在优势。

对于NP完全问题，量子计算提供了以下几个潜在的突破口：

- **量子并行性：**量子计算机可以同时对多个状态进行操作，这可以大幅提升暴力搜索和分支限界法等求解NP完全问题的效率。
- **量子叠加性：**量子比特可以处于多个状态的叠加，这使得量子计算机可以同时探索多个解决方案，从而提高求解效率。

目前，量子计算在NP完全问题求解中的应用还处于早期探索阶段，但已经取得了一些有前景的研究成果。例如，谷歌的研究人员利用量子计算机成功求解了一个小规模的旅行商问题，证明了量子计算在该领域的潜力。

### 5.2 启发式算法的优化

启发式算法是一种通过迭代搜索来求解NP完全问题的算法。与精确算法不同，启发式算法不能保证找到最优解，但通常可以在较短时间内找到一个接近最优的解。

为了进一步提高启发式算法的性能，研究人员一直在探索各种优化技术，包括：

- **自适应搜索：**调整搜索策略以适应问题的特点，提高搜索效率。
- **混合算法：**将启发式算法与其他算法（如精确算法或近似算法）结合，取长补短。
- **参数优化：**通过优化启发式算法的参数，提高算法的性能。

### 5.3 分布式计算的探索

分布式计算是一种利用多台计算机协同工作来求解复杂问题的计算方法。对于NP完全问题，分布式计算可以大幅提升求解效率，尤其是对于规模较大的问题。

分布式计算在NP完全问题求解中的应用主要包括：

- **并行搜索：**将搜索任务分配给多台计算机并行执行，提高搜索效率。
- **负载均衡：**根据计算机的性能动态分配任务，优化计算资源利用率。
- **容错机制：**设计容错机制以应对计算机故障，确保计算过程的稳定性。

分布式计算在NP完全问题求解中的应用已经取得了一些成功的案例。例如，分布式计算平台Folding@home利用数百万台计算机协同工作，成功求解了蛋白质折叠等复杂问题。

# 6. NP完全问题的社会影响

NP完全问题不仅在理论计算机科学领域具有深远的影响，其对社会各方面也产生了广泛的影响，包括：

### 6.1 算法设计与复杂度理论

NP完全问题对算法设计和复杂度理论产生了深远的影响。通过研究NP完全问题，计算机科学家对算法的复杂度有了更深入的理解。这促进了算法设计和分析技术的发展，从而提高了算法的效率和可靠性。

### 6.2 人工智能与机器学习

NP完全问题在人工智能和机器学习领域也扮演着重要的角色。许多人工智能和机器学习算法都涉及到NP完全问题的求解。例如，在机器学习中，训练一个深度神经网络通常需要解决一个NP完全的优化问题。因此，NP完全问题的求解技术对于人工智能和机器学习的发展至关重要。

### 6.3 计算科学与工程

NP完全问题在计算科学和工程领域也得到了广泛的应用。例如，在计算化学中，预测分子的结构通常需要解决一个NP完全的组合优化问题。在工程设计中，优化设计参数以满足特定要求也经常涉及到NP完全问题。因此，NP完全问题的求解技术对于解决计算科学和工程中的复杂问题具有重要的意义。