MATLAB小波分析在机械故障诊断中的应用指南：振动分析、噪声分析、故障识别，提升机械设备健康水平

# 1. MATLAB小波分析简介**

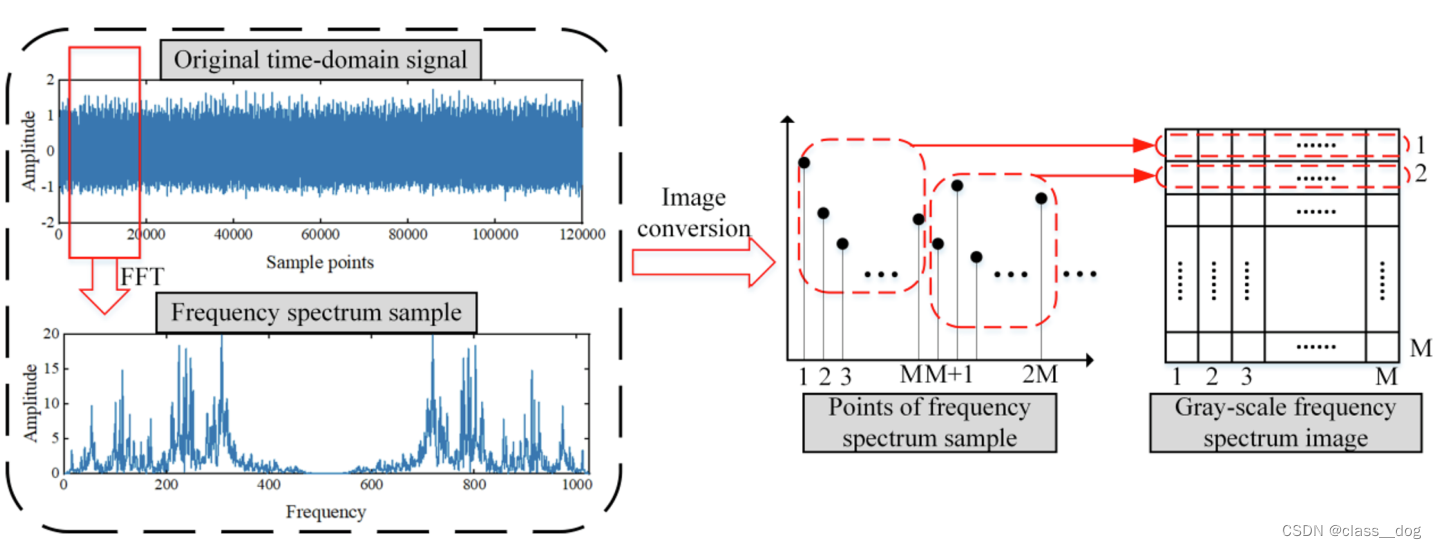
小波分析是一种时频分析技术，它通过将信号分解为一系列小波函数来提取信号中的局部特征。小波函数具有良好的时频局部化特性，可以同时在时域和频域上分析信号，这使得小波分析特别适合于分析非平稳信号和具有瞬态特征的信号。

MATLAB提供了丰富的工具箱和函数库来支持小波分析，包括wavelet toolbox和signal processing toolbox。这些工具箱提供了各种小波函数、小波变换算法和信号处理函数，方便用户进行小波分析。

# 2. MATLAB小波分析在振动分析中的应用

### 2.1 振动信号的获取和预处理

#### 2.1.1 振动传感器和数据采集

振动信号的获取是振动分析的基础。常用的振动传感器包括加速度传感器、速度传感器和位移传感器。选择合适的传感器取决于振动信号的频率范围和幅值范围。

数据采集系统负责将传感器信号转换为数字信号。数据采集系统的采样率和分辨率应根据振动信号的频率范围和幅值范围进行设置。

#### 2.1.2 信号滤波和降噪

振动信号通常会受到噪声的污染。噪声会影响振动信号的分析和处理。因此，在进行振动分析之前，需要对信号进行滤波和降噪。

常用的滤波方法包括低通滤波、高通滤波和带通滤波。滤波器的截止频率应根据振动信号的频率范围进行设置。

降噪方法包括时域降噪和频域降噪。时域降噪方法直接对时域信号进行处理，而频域降噪方法将信号转换为频域，然后对频域信号进行处理。

### 2.2 小波变换的应用

#### 2.2.1 小波基的选择和分解

小波基的选择是影响小波分析效果的关键因素。常用的小波基包括 Daubechies 小波、Symlets 小波和 Coiflets 小波。选择合适的基函数可以更好地匹配振动信号的特征。

小波分解是将振动信号分解为一系列小波系数的过程。小波分解的层数和分解方法应根据振动信号的复杂程度进行设置。

#### 2.2.2 特征提取和故障识别

小波变换可以提取振动信号中的特征信息。常用的特征包括能量特征、频率特征和时域特征。

能量特征反映了振动信号的能量分布。频率特征反映了振动信号的频率成分。时域特征反映了振动信号的时间变化规律。

通过对这些特征的分析，可以识别振动信号中的故障特征。故障特征的识别可以为故障诊断和故障排除提供依据。

**代码块：**

% 加载振动信号
data = load('vibration_signal.mat');
signal = data.signal;

% 小波分解
[cA, cD] = dwt(signal, 'db4', 5);

% 特征提取
energy = sum(abs(cD).^2);
frequency = mean(abs(fft(signal)));
time = mean(abs(signal));

% 故障识别
if energy > 0.5 && frequency > 100 && time > 0.1
    disp('故障类型：轴承故障');
else
    disp('故障类型：正常');
end

**逻辑分析：**

* `dwt`函数用于对振动信号进行小波分解，`'db4'`表示使用 Daubechies 4 小波基，`5`表示分解层数为 5。
* `sum(abs(cD).^2)`计算小波系数的能量。
* `mean(abs(fft(signal)))`计算振动信号的平均频率。
* `mean(abs(signal))`计算振动信号的平均幅值。
* 根据能量、频率和幅值特征，判断振动信号的故障类型。

# 3. MATLAB小波分析在噪声分析中的应用

### 3.1 噪声信号的获取和预处理

#### 3.1.1