集成方法模型评估：Boosting与Bagging性能大比拼

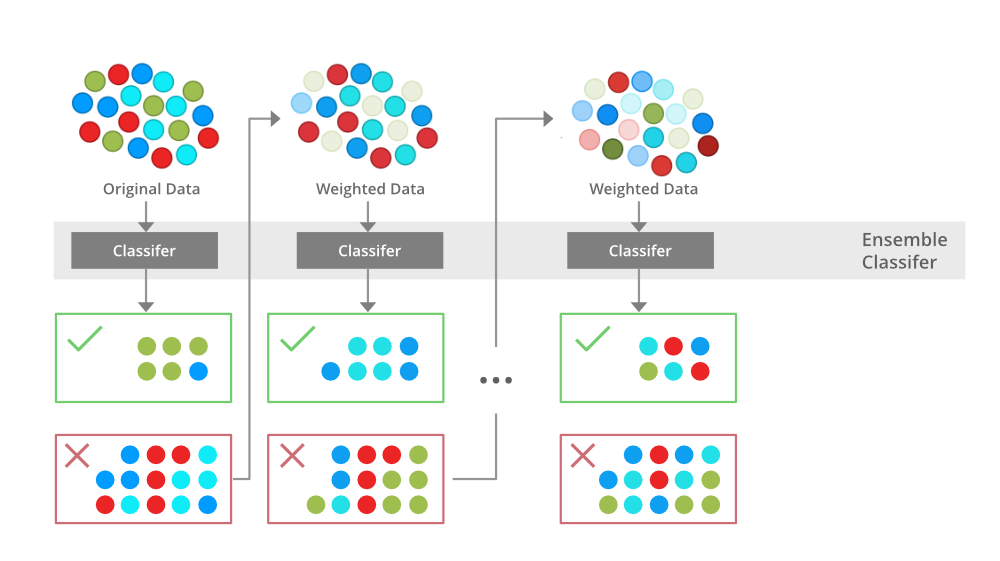
# 1. 集成方法模型概述

集成方法模型是一种将多个模型集成在一起以提高预测准确率和稳定性的方式。它起源于20世纪90年代初，已成为机器学习和数据分析中的核心研究领域之一。集成方法模型的核心思想是“众人拾柴火焰高”，即通过结合多个模型的预测结果，能够得到比单一模型更加准确和鲁棒的总体预测。

## 1.1 集成方法模型的原理

简单来说，集成方法模型是利用“分而治之”的策略，将复杂问题划分为一系列较小的、易于处理的问题，然后单独训练多个学习器来解决这些子问题。在预测阶段，通过一定的策略将各个学习器的预测结果进行组合，以期获得更好的总体性能。

## 1.2 集成方法模型的分类

集成方法模型大致可以分为两大类：Bagging和Boosting。Bagging方法如随机森林，通过减少方差提高模型的稳定性和准确性；而Boosting方法如AdaBoost和XGBoost，通过顺序地训练不同的模型并聚焦于前一个模型预测错误的样本，从而提高模型的准确率。

集成方法模型不仅在机器学习竞赛中得到广泛应用，在现实世界的数据分析中也占据重要地位，因其能够有效提升模型的性能和稳健性。后续章节将分别详细探讨Boosting和Bagging的理论基础、实现步骤及其性能优化策略。

# 2. Boosting算法的原理与实现

### 2.1 Boosting算法理论基础

#### 2.1.1 Boosting的基本概念和分类

Boosting是一类能够将多个弱学习器提升为强学习器的算法。在机器学习中，弱学习器指的是那些性能略优于随机猜测的分类器，而强学习器则是指性能显著高于随机猜测的分类器。Boosting通过组合多个弱学习器来构建一个强学习器，每个弱学习器都侧重于前一个学习器的错误。

Boosting算法主要可以分为两类：数值型Boosting算法和分类型Boosting算法。其中，数值型Boosting算法的代表是AdaBoost（Adaptive Boosting），而分类型Boosting算法的代表则是Gradient Boosting。

#### 2.1.2 Boosting算法的工作原理

Boosting算法的核心思想在于迭代，通过反复训练多个模型，并根据前一个模型的错误来调整后续模型的训练。具体来说，它为每个样本分配一个权重，并在训练过程中不断更新这些权重。错误分类的样本的权重会增加，而正确分类的样本的权重会减少。这样，后续的弱学习器会更加关注那些难以分类的样本。

以下是Boosting算法的工作原理的简化伪代码：

初始化样本权重D_1(i) = 1/n, 对所有样本i
for t = 1, ..., T:
    训练出第t个弱学习器h_t
    计算h_t的错误率ε_t
    计算第t个弱学习器的权重α_t = log((1-ε_t)/ε_t)
    更新样本权重D_t+1(i) = D_t(i) * exp(α_t * y_i * h_t(x_i)) / Z_t
    其中Z_t是归一化常量，用于保证D_t+1是概率分布
最终强学习器H(x) = sign(∑(α_t * h_t(x)))

### 2.2 Boosting算法的实现步骤

#### 2.2.1 算法的初始化过程

初始化阶段，为每个样本分配相同的权重。通常情况下，权重初始化为`1/n`，其中`n`是样本数量。这意味着所有样本在训练初始阶段具有相等的重要性。

#### 2.2.2 弱学习器的构建

弱学习器可以是任何类型的简单模型，如决策树、线性分类器等。在Boosting框架下，每一轮迭代都会训练一个新的弱学习器。算法会根据当前样本权重分配给弱学习器的训练数据。

#### 2.2.3 权重更新与模型集成

每一轮迭代结束后，对于那些被正确分类的样本，其权重会下降；而对于那些被错误分类的样本，其权重则会上升。随着算法的进行，那些难以分类的样本会被赋予更大的关注。最终，所有的弱学习器通过加权求和的方式集成成为最终的强学习器。

### 2.3 Boosting算法的性能优化

#### 2.3.1 超参数调优

Boosting算法中包含多个超参数，例如学习率、弱学习器数量、树的深度等。超参数的选择对模型的性能影响很大。通过交叉验证、网格搜索或随机搜索等方法，可以找到最佳的超参数组合。

#### 2.3.2 防止过拟合的策略

Boosting算法容易过拟合，因为模型会过分关注那些难以分类的样本。为了避免过拟合，可以使用早停（early stopping），即当验证集上的性能不再提升时停止训练。此外，引入正则化项或限制弱学习器的复杂度也能有效防止过拟合。

本章节介绍了Boosting算法的基础理论、实现步骤以及性能优化方法。通过这些内容，我们可以深入了解Boosting的工作机制和实际应用中如何提升其性能，使其在各种机器学习任务中发挥出色的表现。接下来，我们将继续探索另一类集成方法：Bagging算法。

# 3. Bagging算法的原理与实现

## 3.1 Bagging算法理论基础
### 3.1.1 Bagging的基本概念和特性

Bagging（Bootstrap Aggregating）算法是一种通过构建多个模型，并将它们的预测结果进行聚合，以达到降低方差、提高整体模型稳定性和预测准确度的集成学习方法。在Bagging算法中，每个基学习器（base learner）通常是相同的算法，但是在不同的数据子集上进行训练。这些数据子集通过Bootstrap抽样从原始数据集中有放回地随机抽样得到。

具体而言，Bagging算法的特性包括：

- **多样性（Diversity）**：由于每个基学习器是基于不同子集训练的，因此它们之间具有一定程度的差异性，这种差异性使得模型在遇到新数据时能够具有更好的泛化能力。
- **稳定性（Stability）**：聚合多个模型的预测结果，可以有效地减少模型预测的方差，使得整体模型表现更加稳定。
- **独立性（Independence）**：每个基学习器独立训练，互不干扰，这使得Bagging算法易于并行化。

### 3.1.2 Bagging与Bootstrap抽样的关系

Bagging算法的核心是Bootstrap抽样技术，这是一种统计方法，可以对总体样本进行有放回的随机抽样，每次可以重复抽取相同的样本，这样就能生成多个不同的样本子集。通过Bootstrap抽样，我们可以获得含有一定数量重复元素的子集，这些子集的大小与原始数据集相同。

因为抽样是有放回的，所以某些样本可能在一次抽样中被重复选择，而其他一些样本可能一次都未被选中。这种方法产生了高度随机化的样本子集，有助于提高基学习器的差异性，从而使得集成模型在面对数据变化时能保持较好的适应性。

## 3.2 Bagging算法的实现步骤

### 3.2.1 抽样与自助聚合方法

在实现Bagging算法时，首先需要进行Bootstrap抽样，以获取多个数据子集。对于每个子集，执行以下步骤：

1. 从原始数据集中有放回地随机选择N个样本，创建一个新的数据子集。通常N等于原始数据集的大小。
2. 对这个新的数据子集重复上述过程K次，得到K个不同的训练数据子集。

接下来，对每个数据子集训练一个基学习器。这些基学习器可以是决策树、神经网络或任何其他的监督学习模型。因为这些基学习器在不同的数据子集上进行训练，所以它们各自学习到的