贝叶斯分类模型评估：概率视角下的模型表现解析

# 1. 贝叶斯分类模型概述

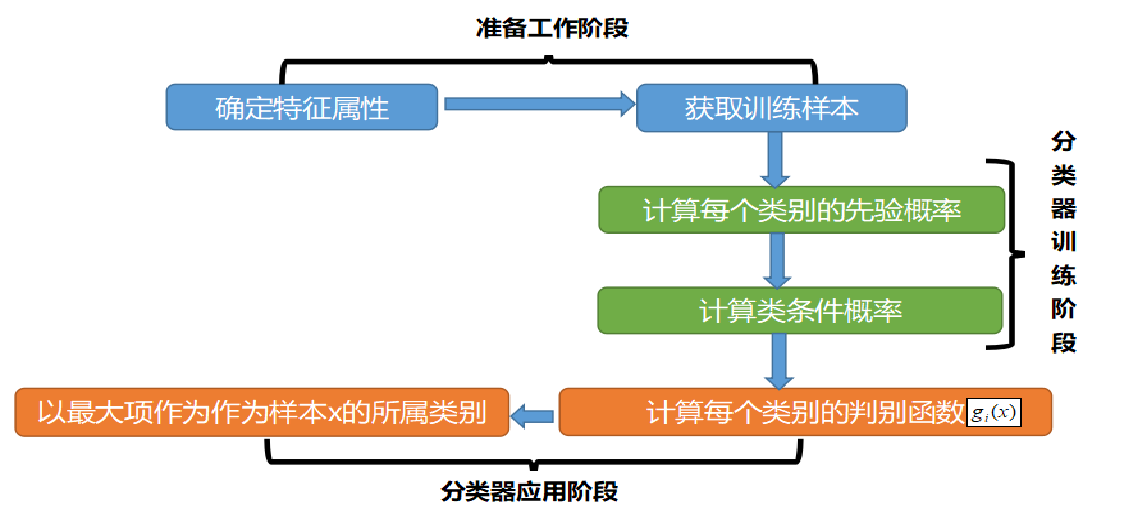
贝叶斯分类模型是一种基于贝叶斯定理的统计分类模型，广泛应用于数据挖掘和机器学习领域。它利用已知的数据信息，通过统计推断来预测未知类别的概率。贝叶斯分类模型的核心思想是：在已知一些条件下，利用贝叶斯定理对类别的概率进行更新，从而预测出最有可能的结果。

贝叶斯分类模型的主要优点是其能够在有限数据的情况下进行有效学习，具有较好的泛化能力。此外，它还可以结合先验知识，提供直观的解释性。然而，选择合适的先验分布和处理高维数据时面临诸多挑战，这些问题将在后续章节中详细讨论。

在实际应用中，贝叶斯分类模型已经被应用于各种场景，包括垃圾邮件识别、疾病诊断、信用评分等。随着计算能力的提高和算法的优化，贝叶斯分类模型在未来有着广阔的应用前景。

# 2. 贝叶斯分类的理论基础

### 2.1 概率论基础

贝叶斯分类方法的理论基础根植于概率论。为了深入理解贝叶斯分类器，首先需要掌握几个关键的概率论概念。

#### 2.1.1 条件概率与独立性

在贝叶斯分类中，条件概率是一个核心概念。条件概率描述了一个事件在另一个事件发生的条件下发生的概率。例如，P(A|B)代表事件B发生时，事件A发生的概率。贝叶斯定理正是在这种条件概率的基础上构建的。

独立性是概率论中的另一个基础概念，指的是两个事件的发生互不影响。如果事件A和事件B独立，则P(A|B) = P(A)。但在现实世界中，往往很难找到完全独立的事件，更多的是存在某种相关性。

#### 2.1.2 全概率公式与贝叶斯定理

全概率公式允许我们通过对一些互斥事件的集合求和来计算一个事件的总概率。如果有事件B1, B2, ..., Bn构成一个完整的事件空间，且它们两两互斥，则全概率公式可表示为：

P(A) = Σ P(A|Bi)P(Bi)

贝叶斯定理则是从全概率公式中发展而来，用于在已知部分条件概率的情况下求解其他条件概率。它将条件概率的顺序颠倒过来，贝叶斯定理公式如下：

P(A|B) = P(B|A)P(A) / P(B)

在贝叶斯分类中，我们通常将待分类的数据点看作事件A，而将已知的数据类别看作事件B，然后利用贝叶斯定理来计算数据点属于每个类别的概率，再将数据点分配到具有最高概率的类别。

### 2.2 贝叶斯决策理论

贝叶斯决策理论是统计决策论中的一类方法，它提供了一个规范的框架来做出最优决策。

#### 2.2.1 贝叶斯最优分类器

贝叶斯最优分类器是一种理论上的最优分类器，它基于贝叶斯定理，对于给定的观测数据，选择具有最高后验概率的类别作为预测结果。它使得分类错误的概率达到最小。

#### 2.2.2 损失函数与后验风险

在决策理论中，损失函数用来量化决策错误的代价，常见的损失函数包括0-1损失函数和平方损失函数。后验风险是在贝叶斯决策框架下，基于给定的损失函数和概率模型来评估决策规则的平均损失。

通过对不同决策结果的风险进行评估，贝叶斯分类器可以优化决策过程，从而达到降低风险的目的。损失函数的选择直接影响了分类器的决策边界，因此在实际应用中需要仔细选择合适的损失函数来符合实际问题的需求。

以上内容构成了贝叶斯分类理论的核心，而在实际应用中，还需要对数据进行深入分析并应用到模型构建中去。下一章，我们将探讨贝叶斯分类模型的评估指标，以确保模型的预测质量和决策准确性。

# 3. 贝叶斯分类模型的评估指标

## 3.1 概率预测的准确性评估

### 3.1.1 概率评分方法

在贝叶斯分类模型中，概率预测的准确性至关重要，因为它直接关系到分类决策的质量。概率评分方法是通过计算模型对样本类别概率预测与实际类别之间差异的评分。该评分方法的一个典型例子是对数似然评分。对数似然评分是对每个类别的概率预测值取自然对数，然后计算所有样本的对数似然的平均值。

import numpy as np

def log_likelihood_score(y_true, y_pred):
    return np.mean(np.log(y_pred[y_true]))

# 假设y_true是真实标签数组，y_pred是预测概率数组
# 例子中的y_pred应是一个二维数组，每个样本的概率预测应对应一行

在上述的代码块中，`log_likelihood_score` 函数通过计算真实标签为正例时的概率的对数，以及真实标签为负例时的概率的对数，来评估模型预测的准确性。最终的评分是对所有样本的对数似然值求平均数。需要注意的是，该函数假设 `y_true` 是由 0 和 1 组成的数组，而 `y_pred` 是一个二维数组，其中每行对应一个样本的概率预测。

### 3.1.2 对数损失与Brier分数

除了对数似然评分之外，对数损失（也称为交叉熵损失）和Brier分数也是常用的概率预测准确性评分方法。对数损失用于衡量模型预测的概率分布与真实分布之间的差异。Brier分数则衡量的是预测概率与实际标签之间差异的平方，它给出了一个介于0和1之间的评分，其中0表示完全准确。

from sklearn.metrics import log_loss, brier_score_loss

# 假设y_true是真实标签数组，y_pred是预测概率数组
# y_pred需要是一个二维数组，每行代表一个样本的预测概率

log_loss_score = log_loss(y_true, y_pred)
brier_score = brier_score_loss(y_true, y_pred)

在上述代码块中，`log_loss` 和 `brier_score_loss` 函数分别计算了对数损失和Brier分数。对数损失适用于多分类问题，而Brier分数可用于二分类或多分类问题。这些评分方法能够给出量化模型预测概率质量的数值，从而可以用来比较不同模型或模型的不同配置之间的性能。

## 3.2 分类性能的评价指标

### 3.2.1 准确率、精确率、召回率和F1分数

准确率、精确率、召回率和F1分数是四个广泛用于分类模型性能评