MATLAB 高斯滤波图像边缘检测应用：原理与实战，精准识别

# 1. 高斯滤波的理论基础**

高斯滤波是一种广泛用于图像处理中的线性平滑滤波器。它基于高斯分布函数，该函数以钟形曲线为特征，中心值最高，向两侧逐渐衰减。

高斯核是高斯滤波器的核心，它是一个二维矩阵，其元素的值与高斯分布函数成正比。高斯核的大小和标准差决定了滤波器的平滑程度。标准差越大，滤波器越平滑。

高斯滤波的数学表达如下：

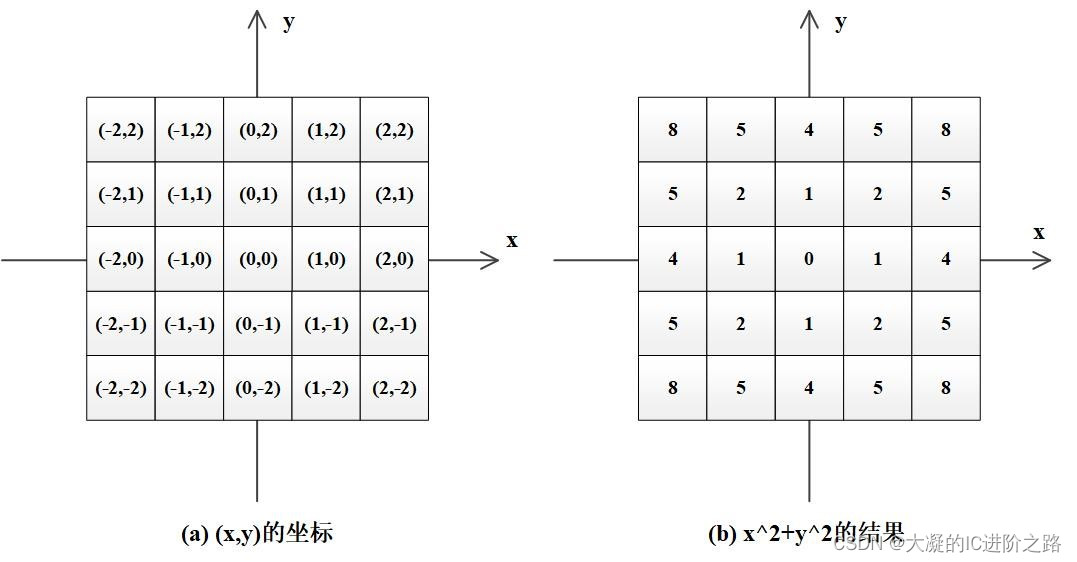
G(x, y) = (1 / (2πσ^2)) * e^(-(x^2 + y^2) / (2σ^2))

其中，G(x, y) 是高斯核的元素值，σ 是标准差，x 和 y 是图像中的坐标。

# 2. 高斯滤波在图像边缘检测中的应用

### 2.1 高斯滤波的原理

#### 2.1.1 高斯核的构造

高斯滤波是一种线性滤波技术，其核心是使用高斯核对图像进行卷积运算。高斯核是一个对称的钟形函数，其权重随着与中心的距离呈指数衰减。

G(x, y) = (1 / (2πσ^2)) * e^(-(x^2 + y^2) / (2σ^2))

其中，σ 为高斯核的标准差，控制着高斯核的形状和大小。

#### 2.1.2 高斯滤波的数学表达

高斯滤波的数学表达为：

F'(x, y) = G(x, y) * F(x, y)

其中，F(x, y) 为原始图像，F'(x, y) 为高斯滤波后的图像。

### 2.2 高斯滤波对图像边缘的影响

#### 2.2.1 边缘模糊化

高斯滤波的主要作用是模糊图像，这包括图像中的边缘。由于高斯核的权重随着与中心的距离呈指数衰减，因此靠近图像边缘的像素受到的权重较小，从而导致边缘模糊化。

#### 2.2.2 噪声抑制

高斯滤波还具有噪声抑制的效果。由于高斯核的权重呈指数衰减，因此噪声像素（通常分布在图像中较小的区域）受到的权重较小，从而被抑制。

### 2.3 高斯滤波在边缘检测中的作用

在图像边缘检测中，高斯滤波通常作为预处理步骤，用于模糊图像并抑制噪声。通过模糊图像，可以减少边缘检测算法对噪声的敏感性，从而提高边缘检测的准确性。

# 3. MATLAB 中的高斯滤波实战

### 3.1 高斯滤波函数的使用

在 MATLAB 中，提供了两种常用的高斯滤波函数：`imgaussfilt` 和 `fspecial`。

#### 3.1.1 imgaussfilt 函数

`imgaussfilt` 函数用于对图像进行高斯滤波。其语法如下：

``