深入理解MATLAB 高斯滤波：数学基础与原理详解

# 1. 高斯滤波的数学基础**

**1.1 高斯分布的特性**

高斯分布，又称正态分布，是一种连续概率分布，其概率密度函数为：

f(x) = (1 / (σ√(2π))) * e^(-(x - μ)² / (2σ²))

其中，μ 为均值，σ 为标准差。高斯分布具有钟形曲线形状，其中心点为 μ，两侧呈对称分布。

**1.2 高斯核的生成**

高斯核是一个二维矩阵，其元素的值与高斯分布的概率密度函数成正比。高斯核的生成通常使用以下公式：

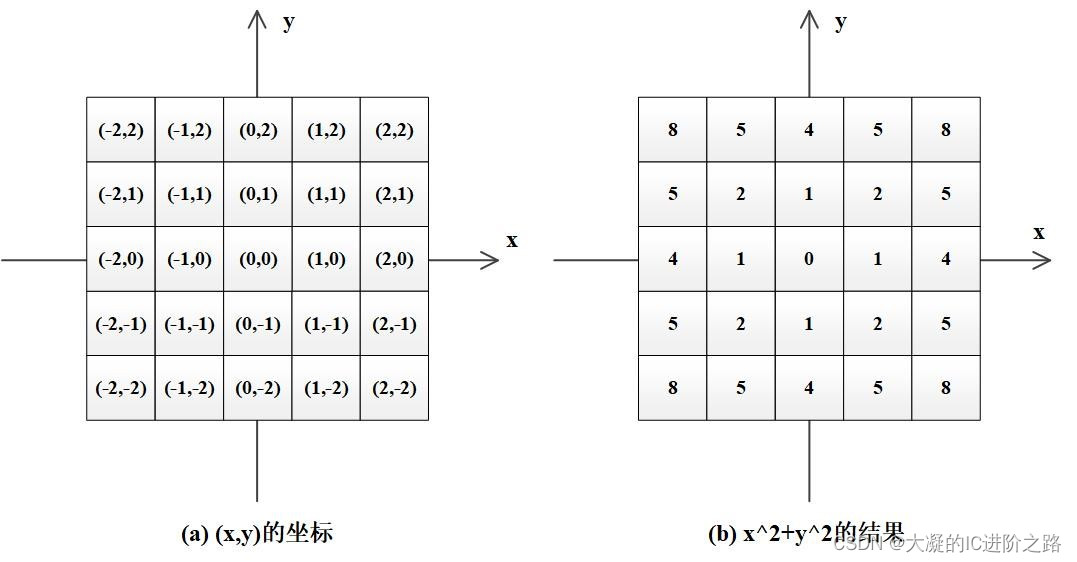
G(x, y) = (1 / (2πσ²)) * e^(-(x² + y²) / (2σ²))

其中，σ 为高斯核的标准差，控制着高斯核的平滑程度。

# 2.1 卷积运算的原理

### 卷积运算的概念

卷积运算是一种数学运算，用于将两个函数（或信号）相乘，然后将其中一个函数反转并沿另一个函数滑动。卷积运算的目的是将输入信号与卷积核（一个权重矩阵）相结合，以提取信号中的特定特征。

### 卷积运算的数学表示

卷积运算可以用数学公式表示为：

f(x) ∗ g(x) = ∫f(t)g(x - t)dt

其中：

* f(x) 是输入信号
* g(x) 是卷积核
* ∗ 表示卷积运算

### 卷积运算的直观解释

直观地，卷积运算可以理解为将卷积核在输入信号上滑动，在每个位置将卷积核与输入信号相乘，然后将结果相加。卷积核的形状和大小决定了提取的特征类型。

### 卷积运算的性质

卷积运算具有以下性质：

* **交换律：** f(x) ∗ g(x) = g(x) ∗ f(x)
* **结合律：** (f(x) ∗ g(x)) ∗ h(x) = f(x) ∗ (g(x) ∗ h(x))
* **分配律：** f(x) ∗ (g(x) + h(x)) = f(x) ∗ g(x) + f(x) ∗ h(x)

## 2.2 高斯滤波的卷积过程

### 高斯滤波的卷积核

高斯滤波使用一个高斯核作为卷积核。高斯核是一个对称的钟形曲线，其形状由标准差 σ 控制。标准差越小，高斯核越窄，提取的特征越精细。

### 高斯滤波的卷积过程

高斯滤波的卷积过程如下：

1. 将高斯核与输入图像相乘。
2. 将高斯核反转并沿输入图像滑动。
3. 在每个位置，将反转的高斯核与输入图像相乘，并将结果相加。
4. 重复步骤 1-3，直到高斯核覆盖整个输入图像。

### 卷积过程的代码实现

以下 MATLAB 代码展示了高斯滤波的卷积过程：

% 定义输入图像
image = imread('image.jpg');

% 生成高斯核
sigma = 2;
kernel = fspecial('gaussian', [5 5], sigma);

% 进行卷积运算
filtered_image = conv2(image, kernel, 'same');

% 显示结果
imshow(filtered_image);

### 卷积过程的逻辑分析

* `conv2` 函数执行卷积运算。
* `'same'` 参数指定输出图像的大小与输入图像相同。
* 卷积运算的结果存储在 `filtered_image` 中。

## 2.3 高斯滤波的平滑效果

### 高斯滤波的平滑作用

高斯滤波的主要作用是平滑图像，去除图像中的噪声和细节。高斯核的形状决定了平滑的程度。标准差越小，平滑效果越明显。

### 平滑效果的数学解释

卷积运算的数学表达式表明，高斯滤波的平滑效果是由高斯核的加权平均引起的。高斯核的中心权重最高，随着距离中心的增加，权重逐渐减小。因此，当高斯核与输入图像