揭秘MATLAB 高斯滤波：原理、实现与实战应用，一站式掌握

# 1. MATLAB 高斯滤波的理论基础

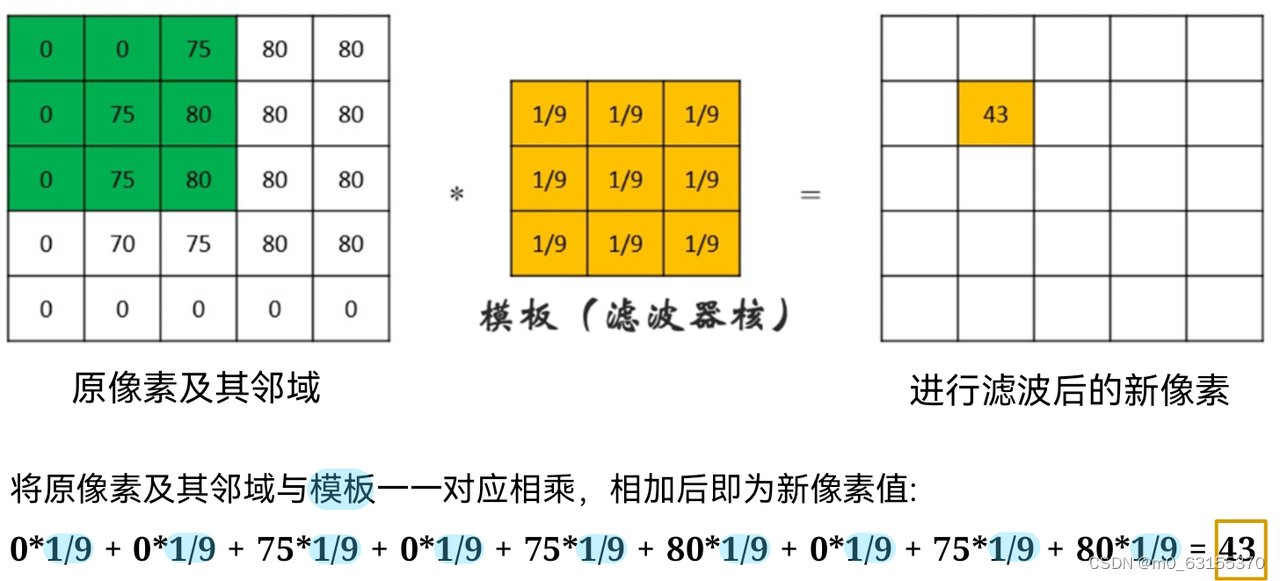
高斯滤波是一种广泛应用于图像处理中的平滑滤波技术，其原理是使用高斯核对图像进行卷积运算。高斯核是一个对称的钟形函数，其形状由标准差 σ 控制。

在数学上，高斯核的公式为：

G(x, y) = (1 / (2πσ^2)) * exp(-(x^2 + y^2) / (2σ^2))

其中，(x, y) 是高斯核中的坐标，σ 是标准差。

卷积运算是一种数学运算，它将图像中的每个像素与高斯核进行加权平均。通过这种运算，高斯滤波可以有效地消除图像中的噪声和模糊边缘，同时保留图像的重要特征。

# 2. MATLAB 高斯滤波的实现技巧

### 2.1 高斯核的生成和选择

#### 2.1.1 高斯核的数学原理

高斯核是一个对称的钟形曲线，其数学表达式为：

G(x, y) = (1 / (2πσ^2)) * exp(-(x^2 + y^2) / (2σ^2))

其中，σ 是高斯核的标准差，控制着核的宽度和形状。

#### 2.1.2 高斯核的生成方法

MATLAB 中提供了 `fspecial('gaussian', [m, n], sigma)` 函数来生成高斯核。其中，`[m, n]` 指定核的大小，`sigma` 指定标准差。

### 2.2 图像卷积操作

#### 2.2.1 卷积的数学定义

卷积是一种数学运算，用于将两个函数（图像和核）相乘并求和，得到一个新的函数。在图像处理中，卷积用于应用核的权重对图像进行平滑、锐化或其他操作。

#### 2.2.2 MATLAB 中的卷积函数

MATLAB 中提供了 `conv2(image, kernel)` 函数来执行图像卷积。其中，`image` 是输入图像，`kernel` 是卷积核。

### 2.3 边界处理策略

在进行图像卷积时，需要考虑图像边界的问题。边界处理策略决定了核在图像边缘如何应用。

#### 2.3.1 零填充

零填充策略将图像边界填充为零值。这会导致图像边缘出现伪影。

#### 2.3.2 对称填充

对称填充策略将图像边界填充为图像本身的镜像。这可以减少伪影，但可能会引入边缘重复。

#### 2.3.3 镜像填充

镜像填充策略将图像边界填充为图像本身的镜像，但镜像是翻转的。这可以进一步减少伪影，但可能会引入边缘失真。

% 图像
image = imread('image.jpg');

% 高斯核
sigma = 2;
kernel = fspecial('gaussian', [5, 5], sigma);

% 卷积操作
blurred_image = conv2(image, kernel, 'same');

% 显示结果
figure;
subplot(1, 2, 1);
imshow(image);
title('原始图像');
subplot(1, 2, 2);
imshow(blurred_image);
title('高斯滤波后的图像');

# 3. MATLAB 高斯滤波的实战应用

### 3.1 图像降噪

#### 3.1.1 高斯滤波在图像降噪中的原理

图像降噪是图像处理中一项基本任务，其目的是去除图像中的噪声，提高图像质量。高斯滤波是一种有效的图像降噪技术，其原理是利用高斯核对图像进行卷积操作。

高斯核是一个对称的钟形曲线，其权重从中心向外逐渐减小。当高斯核与图像卷积时，图像中的噪声成分会被平滑，而图像中的重要特征（如边缘和纹理）则会被保留。

#### 3.1.2 MATLAB 中的图像降噪示例

在 MATLAB 中，可以使用 `imnoise` 函数向图像添加噪声，并使用 `imgaussfilt` 函数进行高斯滤波降噪。以下代码演示了如何使用 MATLAB 对图像进行高斯滤波降噪：

% 读取图像
image = imread('image.jpg');

% 添加噪声
noisy_image = imnoise(image, 'gaussian', 0.05);

% 高斯滤波降噪
filtered_image = imgaussfilt(noisy_image, 2);

% 显示结果
subplot(1, 3, 1);
imshow(image);
title('原始图像');

subplot(1, 3, 2);
imshow(noisy_image);
title('带噪声图像');

subplot(1, 3, 3);
imshow(filtered_image);
title('高斯滤波降噪后图像');

### 3.2 图像模糊

#### 3.2.1 高斯滤波在图像模糊中的原理

图像模糊是图像处理中另一种常见操作，其目的是使图像变得模糊或柔和。高斯滤波也可以用于图像模糊，其原理与图像降噪类似。

当高斯核的标准差较大时，高斯滤波的平滑效果更明显，图像会变得更加模糊。通过调整高斯核的标准差，可以控制图像模糊的程度。

#### 3.2.2 MATLAB 中的图像模糊示例

以下代码演示了如何使用 MATLAB 对图像进行高斯滤波模糊：

% 读取图像
image = imread('image.jpg');

% 高斯滤波模糊
blurred_image = imgaussfilt(image, 5);

% 显示结果
subplot(1, 2, 1);
imshow(image);
title('原始图像');

subplot(1, 2, 2);
imshow(blurred_image);
title('高斯滤波模糊后图像');

### 3.3 图像边缘检测

#### 3.3.1 高斯滤波在图像边缘检测中的原理

图像边缘检测是图像处理中的一项重要技术，其目的是检测图像中的边缘和轮廓。高斯滤波可以作为图像边缘检测的预处理步骤，其作用是平滑图像，去除噪声，从而提高边缘检测的准确性。

#### 3.3.2 MATLAB 中的图像边缘检测示例

以下代码演示了如何使用 MATLAB 对图像进行高斯滤波预处理，然后进行边缘检测：

% 读取图像
image = imread('image.jpg');

% 高斯滤波预处理
filtered_image = imgaussfilt(image, 2);

% 边缘检测
edges = edge(filtered_image, 'canny');

% 显示结果
subplot(1, 2, 1);
imshow(image);
title('原始图像');

subplot(1, 2, 2);
imshow(edges);
title('高斯滤波预处理后边缘检测结果');

# 4. MATLAB 高斯滤波的进阶应用

### 4.1 多尺度高斯滤波

**4.1.1 多尺度高斯滤波的原理**

多尺度高斯滤波是一种通过使用不同尺度的多个高斯核对图像进行卷积来处理图像的技术。它可以帮助提取图像中不同尺度的特征，从而实现更鲁棒和准确的图像处理结果。

**4.1.2 MATLAB 中的多尺度高斯滤波实现**

% 定义图像
image = imread('image.jpg');

% 定义不同尺度的标准差
scales = [1, 2, 4, 8, 16];

% 存储多尺度滤波后的图像
filteredImages = cell(1, length(scales));

% 遍历不同尺度
for i = 1:length(scales)
    % 生成高斯核
    kernel = fspecial('gaussian', 5, scales(i));
    % 进行卷积操作
    filteredImage = imfilter(image, kernel);
    % 存储滤波后的图像
    filteredImages{i} = filteredImage;
end

### 4.2 高斯混合模型

**4.2.1 高斯混合模型的数学基础**

高斯混合模型 (GMM) 是一种概率模型，它假设数据是由多个高斯分布的混合组成。它可以用于对数据进行聚类、分类和密度估计。

**4.2.2 MATLAB 中的高斯混合模型实现**

% 加载数据
data = load('data.mat');

% 创建高斯混合模型对象
gm = fitgmdist(data, 3);

% 预测数据所属的类别
labels = cluster(gm, data);

% 可视化聚类结果
figure;
scatter(data(:,1), data(:,2), 50, labels, 'filled');

### 4.3 图像分割

**4.3.1 高斯滤波在图像分割中的原理**

高斯滤波可以用于图像分割，因为它可以平滑图像并消除噪声，从而使分割算法更容易识别图像中的不同区域。

**4.3.2 MATLAB 中的图像分割示例**

% 加载图像
image = imread('image.jpg');

% 转换为灰度图像
grayImage = rgb2gray(image);

% 高斯滤波
filteredImage = imgaussfilt(grayImage, 2);

% 使用阈值分割
segmentedImage = im2bw(filteredImage, 0.5);

% 显示分割结果
figure;
imshow(segmentedImage);

# 5. MATLAB 高斯滤波的性能优化

### 5.1 并行化处理

**5.1.1 MATLAB 中的并行化编程**

MATLAB 提供了并行计算工具箱，支持多核处理器和分布式计算。并行化处理可以将任务分解为多个子任务，并行执行，从而提高计算效率。

**5.1.2 高斯滤波的并行化实现**

高斯滤波是一个计算密集型操作，可以并行化以提高性能。MATLAB 中可以使用 `parfor` 循环来实现并行化：

% 创建高斯核
h = fspecial('gaussian', [5, 5], 1);

% 获取图像数据
I = imread('image.jpg');

% 创建并行池
parpool;

% 并行执行高斯滤波
I_filtered = zeros(size(I));
parfor i = 1:size(I, 1)
    for j = 1:size(I, 2)
        I_filtered(i, j) = sum(sum(h .* I(i-2:i+2, j-2:j+2)));
    end
end

% 关闭并行池
delete(gcp);

### 5.2 算法优化

**5.2.1 快速傅里叶变换**

快速傅里叶变换 (FFT) 是一种快速计算离散傅里叶变换 (DFT) 的算法。FFT 可以将图像卷积操作转换为频域，从而提高计算效率。

**5.2.2 分离卷积**

分离卷积是一种将二维卷积分解为两个一维卷积的算法。分离卷积可以减少计算量，提高性能。

% 使用 FFT 进行高斯滤波
I_filtered = real(ifft2(fft2(I) .* fft2(h)));

% 使用分离卷积进行高斯滤波
h_x = h(:, 1);
h_y = h(1, :);
I_filtered = conv2(I, h_x, 'same');
I_filtered = conv2(I_filtered, h_y', 'same');