MATLAB 高斯滤波图像增强应用：提升图像质量，一招制胜

# 1. 图像增强概述**

图像增强是一种图像处理技术，旨在改善图像的视觉质量，使其更易于理解和分析。图像增强通常用于以下目的：

* 提高对比度和亮度，使图像更清晰
* 去除噪声，改善图像质量
* 锐化图像，突出细节
* 调整色彩平衡，使图像更自然

图像增强技术有很多种，每种技术都有其独特的优点和缺点。在选择图像增强技术时，需要考虑图像的具体需求和应用。

# 2. 高斯滤波原理与应用

### 2.1 高斯滤波的数学基础

高斯滤波是一种线性滤波器，其核心思想是使用高斯函数作为滤波器核，对图像进行卷积运算。高斯函数是一个钟形曲线，其数学表达式为：

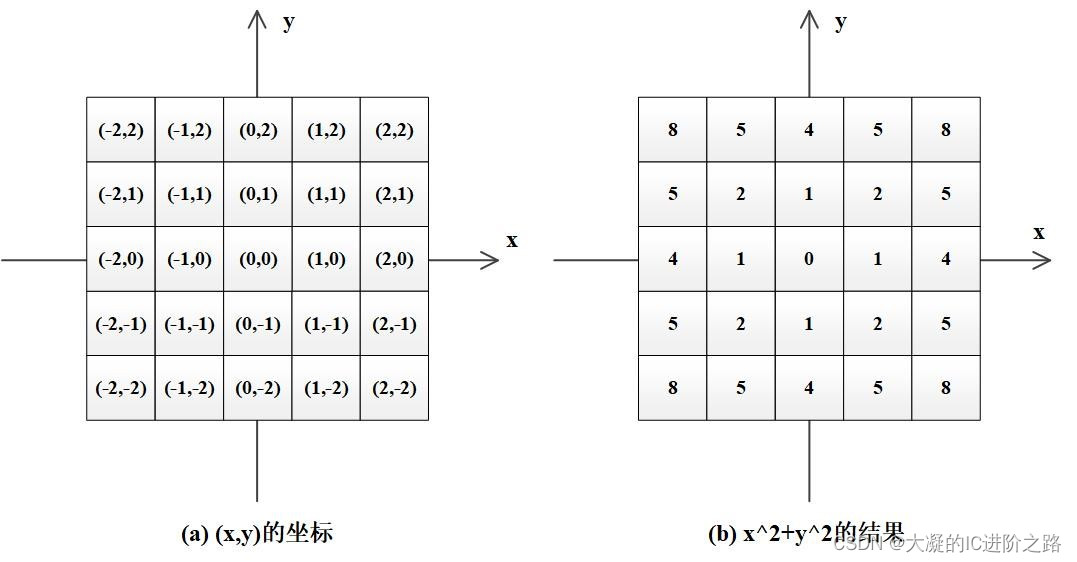
G(x, y) = (1 / (2πσ^2)) * e^(-(x^2 + y^2) / (2σ^2))

其中，σ 是高斯函数的标准差，控制着滤波器的平滑程度。σ 值越大，滤波效果越平滑；σ 值越小，滤波效果越锐利。

### 2.2 高斯滤波的图像增强效果

高斯滤波在图像增强中主要用于图像去噪和图像锐化。

**图像去噪：**高斯滤波可以有效去除图像中的高频噪声，同时保留图像的边缘和纹理信息。这是因为高斯函数的平滑特性可以抑制噪声信号，而边缘和纹理信息通常具有较高的频率。

**图像锐化：**高斯滤波也可以用于图像锐化，但需要对滤波器核进行反转。反转后的高斯函数具有一个中心凸起，可以增强图像的边缘和纹理信息。

### 2.2.1 高斯滤波的数学推导

高斯滤波的数学推导过程如下：

1. **卷积运算：**高斯滤波本质上是一个卷积运算，即输入图像与高斯函数的卷积。卷积运算的数学表达式为：

f(x, y) * G(x, y) = ∫∫ f(u, v) * G(x - u, y - v) du dv

其中，f(x, y) 是输入图像，G(x, y) 是高斯函数。

2. **高斯函数的离散化：**由于计算机只能处理离散数据，因此需要将高斯函数离散化。离散化的高斯函数可以表示为：

G[i, j] = (1 / (2πσ^2)) * e^(-(i^2 + j^2) / (2σ^2))

其中，i 和 j 是离散化的坐标。

3. **卷积运算的实现：**离散化的高斯函数可以与输入图像进行卷积运算，得到滤波后的图像。卷积运算的实现可以通过以下步骤：

for i = 1:width
    for j = 1:height
        filtered_image[i, j] = 0;
        for u = 1:kernel_width
            for v = 1:kernel_height
                filtered_image[i, j] += input_image[i + u - 1, j + v - 1] * G[u, v];
            end
        end
    end
end

其中，input_image 是输入图像，kernel_width 和 kernel_height 是高斯滤波器核的大小。

### 2.2.2 高斯滤波的代码示例

以下代码示例演示了如何使用 MATLAB 实现高斯滤波：

% 输入图像
input_image = imread('input.jpg');

% 高斯滤波器核的大小
kernel_size = 5;

% 高斯滤波器核的标准差
sigma = 1;

% 生成高斯滤波器核
kernel = fspecial('gaussian', kern