初识BP神经网络：概念与基本原理

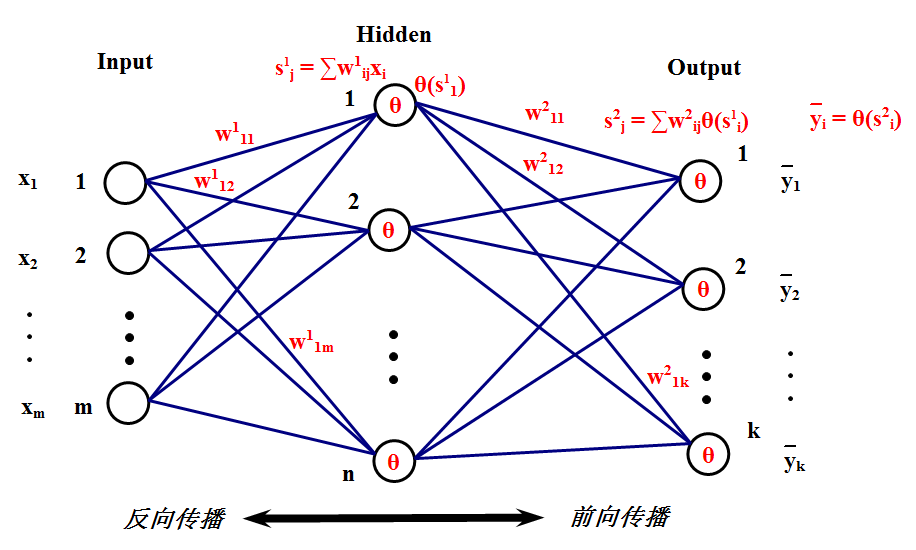
![初识BP神经网络：概念与基本原理](https://img-blog.csdn.net/20150321122210091) # 1.1 人工神经网络简介人工神经网络是一种模仿人类神经网络功能的计算模型，由大量相互连接的人工神经元组成。神经网络通过学习历史数据来建立输入和输出之间的映射关系，从而实现各种复杂的模式识别和预测任务。神经元模型是神经网络的基本单元，包括输入信号加权求和、激活函数处理和输出传递三个步骤。神经网络包括输入层、隐藏层和输出层，隐藏层可以有多层。感知器是最简单的神经网络模型，由输入层和输出层组成。神经网络的训练基于梯度下降算法，通过不断调整网络参数来最小化损失函数，实现模型的优化和更新。通过反向传播算法，可以高效地更新神经网络的权重和偏置项。 # 2. **第二章 BP神经网络的网络结构** ### **2.1 多层感知器（MLP）** 多层感知器（Multilayer Perceptron, MLP）是一种常见的前馈神经网络模型，由一个输入层、一个或多个隐藏层和一个输出层组成。在神经网络中，每个神经元与前一层所有神经元相连，信息单向传播。 #### **2.1.1 输入层** 在多层感知器中，输入层负责接收外部输入，传递给下一层。激活函数用于计算神经元的输出值，常用的激活函数有 Sigmoid、ReLU 等。输入特征是神经网络的输入数据，如图像像素值、文本特征等。 ```python # 示例：Sigmoid 激活函数实现 import numpy as np def sigmoid(x): return 1 / (1 + np.exp(-x)) ``` #### **2.1.2 隐藏层** 隐藏层用于提取数据中的高级特征，进行非线性变换。激活函数的选择对网络性能影响显著，如使用ReLU可解决梯度消失问题。隐藏层包括多个神经元，神经元数量的确定需根据具体问题和计算资源进行选择。 #### **2.1.3 输出层** 输出层负责将隐藏层学到的特征通过一定的方式转换为最终输出。输出编码是指对输出值的编码方式，如分类问题可使用 One-Hot 编码，回归问题可直接输出数值。选择合适的损失函数有助于网络学习目标。 ```python # 示例：交叉熵损失函数实现 def cross_entropy_loss(y_pred, y_true): epsilon = 1e-9 y_pred = np.clip(y_pred, epsilon, 1. - epsilon) return -np.sum(y_true * np.log(y_pred)) ``` ### **2.2 优化方法** 神经网络的训练过程离不开优化算法，其中最常用的是梯度下降法。梯度下降通过反向传播更新网络参数，使损失函数最小化。学习率是梯度下降算法的重要超参数，它决定了参数更新的步长。 ```python # 示例：梯度下降参数更新 def gradient_descent_update(parameters, gradients, learning_rate): for param, grad in zip(parameters, gradients): param -= learning_rate * grad ``` #### **2.2.1 小批量随机梯度下降** 小批量随机梯度下降（Mini-batch Stochastic Gradient Descent）是梯度下降算法的改进版，每次更新参数时不再使用全部数据，而是随机选取一小部分样本计算梯度。 ```python # 示例：小批量随机梯度下降 def mini_batch_sgd(X, y, batch_size, learning_rate, epochs): for epoch in range(epochs): for i in range(0, len(X), batch_size): X_batch = X[i:i+batch_size] y_batch = y[i:i+batch_size] # 计算梯度并更新参数 ``` #### **2.2.2 Adam 优化算法** Adam 是一种自适应学习率的优化算法，结合了动量梯度下降和RMSProp算法。它可以根据历史梯度自适应地调整每个参数的学习率。 ```python # 示例：Adam 优化算法 def adam_optimizer(parameters, gradients, v, s, t, beta1=0.9, beta2=0.999, epsilon=1e-8): for i in range(len(parameters)): v[i] = beta1 * v[i] + (1 - beta1) * gradients[i] s[i] = beta2 * s[i] + (1 - beta2) * (gradients[i] ** 2) v_corrected = v[i] / (1 - beta1**t) s_corrected = s[i] / (1 - beta2**t) parameters[i] -= learning_rate * v_corrected / (np.sqrt(s_corrected) + epsilon) ``` # 3. 第三章反向传播算法的详解 #### 3.1 反向传播的前向计算在神经网络的学习过程中，反向传播算法是十分关键的一环。其中的前向计算是整个算法的起点，通过前向计算，神经网络能够逐层计算并传递输入数据，最终得到输出值。这一过程包含了输入特征的传递和隐藏层的计算两个阶段。 ##### 3.1.1 前向传播过程在前向传播过程中，输入数据从输入层逐层传递至输出层，经过激活函数的作用，最终得到输出值。这个过程包含了输入特征的传递和隐藏层中神经元的计算。 - 3.1.1.1 输入特征传递神经网络的输入层接收外部输入的特征，然后将这些特征传递给下一层。输入特征的传递是神经网络中信息流动的起始点。 - 3.1.1.2 隐藏层计算隐藏层是神经网络中用于提取特征的部分，隐藏层中的神经元计算接收到的输入，并通过激活函数将结果传递给下一层。 ##### 3.1.2 输出层计算输出层的计算是前向传播过程的最后一步，通过输出层的计算得到最终的输出值。这一阶段主要包括了输出值的计算和损失函数的计算。 - 3.1.2.1 输出值计算输出值的计算是根据隐藏层传递过来的值，经过输出层的激活函数后得到的结果。这个结果将被用来计算损失函数。 - 3.1.2.2 损失函数计算损失函数是用来评估模型输出值与实际标签之间的差距，计算损失函数有助于调整神经网络的参数，以提升模型性能。 #### 3.2 反向传播的反向计算在神经网络的训练过程中，反向传播算法通过反向计算来更新神经网络的参数，不断优化模型以提高性能。反向计算阶段涵盖了梯度下降算法和权重调整两个重要部分。 ##### 3.2.1 梯度下降算法梯度下降是一种通过调整模型参数来最小化损失函数的方法，它是反向传播算法中的核心部分。其中包括了权重更新和学习率等重要概念。 - 3.2.1.1 权重更新权重更新是梯度下降算法的关键步骤，通过计算损失函数对权重的偏导数来更新权重值，使模型朝着损失最小化的方向调整。 - 3.2.1.2 学习率学习率是梯度下降算法中控制参数更新步长的重要超参数，合适的学习率可以加快收敛速度，而过大或过小的学习率都会影响模型训练效果。 ##### 3.2.2 权重调整在反向传播算法中，权重调整是根据梯度下降算法计算得到的梯度信息，通过更新权重值来提升神经网络的性能。 - 3.2.2.1 权重调整公式权重调整的公式基于损失函数对权重的梯度计算，包括了权重更新的公式和更新规则，确保模型参数向着降低损失的方向调整。 - 3.2.2.2 偏置项更新除了权重的更新，偏置项也是神经网络中需要调整的参数之一，通过更新偏置项，可以更好地拟合数据，提高模型的泛化能力。 # 4. BP神经网络的训练与调优在构建和训练神经网络模型时，数据预处理是至关重要的一环。良好的数据预处理可以提高模型的训练效果，加快收敛速度，并提高泛化能力。 #### 4.1 数据预处理在神经网络训练之前，数据预处理是必不可少的步骤，可以减少数据中的噪音，提高模型的准确性和效率。 1. **特征缩放** 特征缩放是将数据特征按比例缩放，使其落入一个特定的范围。常用的特征缩放方法包括最小-最大缩放和标准化。最小-最大缩放将特征缩放到\[0, 1\]的范围内，而标准化则通过均值和标准差来缩放数据。 2. **数据标准化** 数据标准化是指对数据进行零均值化处理，使数据分布接近标准正态分布。标准化可以加速神经网络的训练过程，提高模型的预测性能。 3. **数据集划分** 将数据集划分为训练集、验证集和测试集是为了评估模型的泛化能力。通常采用的比例是70%的数据用于训练，10%用于验证，20%用于测试。 #### 4.2 神经网络训练过程在进行神经网络训练时，需要注意模型的过拟合和欠拟合问题，以及如何调优模型参数，以达到最佳的训练效果。 1. **训练集、验证集与测试集** 训练集用于模型参数的学习，验证集用于调整模型的超参数，测试集用于评估模型的性能。交叉验证是一种常用的评估模型性能的方法，可以有效避免过拟合。 2. **过拟合与欠拟合** 过拟合指模型在训练集上表现很好，但在测试集上表现很差；欠拟合则是模型无法在训练集上达到理想的性能。为了解决过拟合问题，可以采用正则化方法或者Dropout技术来减少模型的复杂度。 3. **正则化方法** 正则化是通过在损失函数中加入正则项，限制模型的复杂度，防止过拟合。常见的正则化方法包括L1正则化和L2正则化，可以有效地提高模型的泛化能力。在神经网络的训练和调优过程中，数据预处理和模型优化是非常关键的步骤。合适的数据预处理可以提高模型的训练速度和精度，而有效的调优方法可以优化模型的泛化能力和性能。通过不断优化数据预处理和模型训练过程，可以构建出更加准确和稳健的神经网络模型。 # 5.1 BP神经网络在图像识别中的应用在图像识别领域，BP神经网络作为一种监督学习算法，已经取得了许多成果。下面将详细介绍BP神经网络在图像识别中的应用，主要包括图像特征提取和深度学习与卷积神经网络。 #### 5.1.1 图像特征提取图像识别的关键在于有效地提取图像的特征，传统的方法主要基于人工设计的特征提取器，如HOG、SIFT等。而BP神经网络通过多层隐藏层的组合学习，可以在一定程度上自动提取图像中的特征，无需手动设计。在实际应用中，可以使用预训练的卷积神经网络（CNN）作为特征提取器，将最后一个全连接层之前的输出作为图像的特征表示，然后连接一个BP神经网络用于分类任务。 #### 5.1.2 深度学习与卷积神经网络卷积神经网络（CNN）作为深度学习领域的重要分支，在图像识别任务中表现出色。它通过卷积层和池化层提取图像的局部特征，并通过多层神经网络学习高级特征。下面是一个简单的卷积神经网络示例代码，用于图像分类任务： ```python import tensorflow as tf # 构建卷积神经网络模型 model = tf.keras.models.Sequential([ tf.keras.layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)), tf.keras.layers.MaxPooling2D((2, 2)), tf.keras.layers.Flatten(), tf.keras.layers.Dense(128, activation='relu'), tf.keras.layers.Dense(10, activation='softmax') ]) # 编译模型 model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy']) # 训练模型 model.fit(train_images, train_labels, epochs=10) ``` 在以上示例中，我们使用了一个简单的卷积神经网络模型，通过多次迭代训练（epochs=10）来提高模型的准确性。通过不断优化网络结构和训练参数，BP神经网络在图像识别应用中有着广阔的发展前景。 ### 流程图示例 ```mermaid graph TD A[图像输入] --> B{BP神经网络} B --> |特征提取| C[隐藏层] C --> |特征融合| D[输出层] ``` 综上所述，BP神经网络在图像识别中的应用为我们提供了一种强大而灵活的工具，通过不断迭代和优化，可以实现更加准确和高效的图像识别任务。