贪心算法在 Huffman 编码中的应用：高效数据压缩技术的揭秘

# 1. 数据压缩技术概述**

数据压缩是一种将数据表示为更紧凑形式的技术，以减少存储或传输所需的比特数。它在计算机科学中广泛应用，例如存储、通信和多媒体处理。数据压缩算法通常分为两大类：无损压缩和有损压缩。无损压缩可以完美地重建原始数据，而有损压缩则允许一定程度的失真以获得更高的压缩率。

# 2.1 贪心算法的定义和特点

### 定义

贪心算法是一种求解优化问题的启发式算法，它在每次决策中都选择当前看来最优的方案，而不考虑该方案对后续决策的影响。

### 特点

* **局部最优性：**贪心算法专注于当前局部最优解，而不会考虑全局最优解。
* **快速性：**贪心算法通常具有较快的运行时间，因为它只考虑当前决策，而无需回溯或枚举所有可能的情况。
* **简单性：**贪心算法易于理解和实现，因为它遵循直观的步骤，无需复杂的数学计算。

### 适用场景

贪心算法适用于以下场景：

* **子问题独立：**每个子问题的最优解不依赖于其他子问题的解。
* **最优子结构：**问题的最优解包含其子问题的最优解。
* **贪心选择性质：**每次局部最优的选择最终导致全局最优解。

**代码示例：**

def greedy_knapsack(items, capacity):
    """
    贪心算法求解背包问题。

    参数：
        items: 物品列表，每个物品有重量和价值。
        capacity: 背包容量。

    返回：
        背包中物品的价值之和。
    """
    items.sort(key=lambda item: item.value / item.weight, reverse=True)

    total_value = 0
    current_weight = 0

    for item in items:
        if current_weight + item.weight <= capacity:
            total_value += item.value
            current_weight += item.weight
        else:
            remaining_capacity = capacity - current_weight
            total_value += remaining_capacity * (item.value / item.weight)
            break

    return total_value

**逻辑分析：**

* 将物品按价值密度（价值/重量）降序排序。
* 遍历物品列表，依次将物品装入背包。
* 如果物品重量超过剩余容量，则按价值密度比例装入剩余容量。
* 返回背包中物品的价值之和。

**参数说明：**

* `items`: 物品列表，每个物品包含 `weight` 和 `value` 属性。
* `capacity`: 背包容量。

# 3.1 Huffman 树的构造原理

Huffman 树是一种二叉树，用于表示字符集中的字符及其频率。其构造原理如下：

1. **初始化：**将每个字符及其频率作为叶子节点，创建一组单节点树。
2. **选择：**从单节点树中选择两个具有最小频率的树，将其作为子树。
3. **合并：**创建新的根节点，其频率等于两个子树频率之和。将两个子树作为新根节点的左子树和右子树。
4. **重复：**重复步骤 2 和 3，直到所有单节点树合并为一棵二叉树。

**示例：**

给定字符集 {A, B, C, D, E} 及其频率 {4, 2, 6, 3, 1}，构造 Huffman 树：

1. 初始化：创建 5 个单节点树：

   A: 4
   B: 2
   C: 6
   D: 3
   E: 1

2. 选择：选择频率最小的两个树，即 E 和 B。

3. 合并：创建新根节点，频率为 3（E 和 B 的频率之和）。将 E 和 B 分别作为新根节点的左子树和右子树。

4. 重复：重复步骤 2 和 3，直到所有单节点树合并。

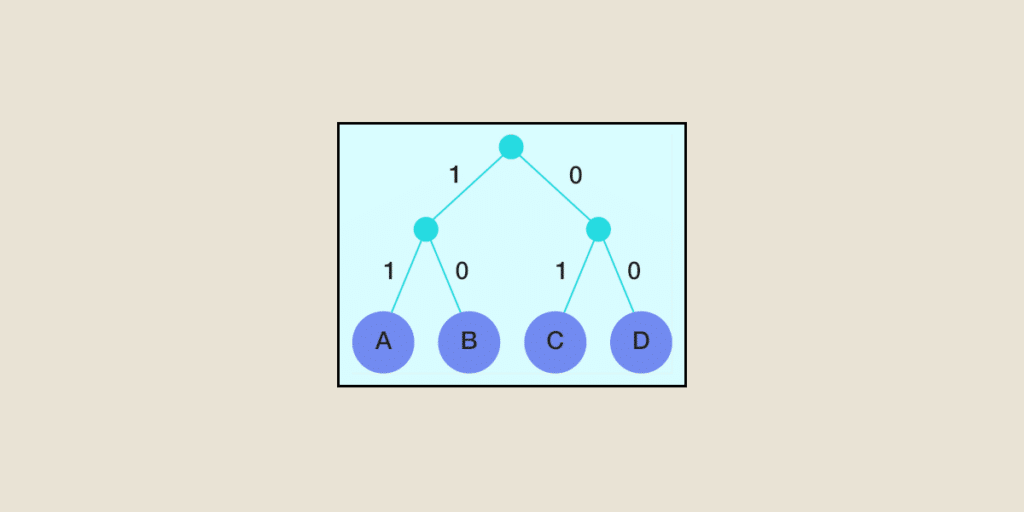
最终得到的 Huffman 树如下：

          (13)
         /    \
       (9)    4
      /   \
     (5)   2
    /   \