贪心算法在 Kruskal 算法中的应用：构建最小生成树的技巧

# 1. 贪心算法概述

贪心算法是一种启发式算法，它通过在每一步中做出局部最优的选择来解决优化问题。这种算法的优点是简单易懂，实现成本低，并且在某些情况下可以获得较好的近似解。

贪心算法的思想是：在解决问题时，总是做出当前看来最好的选择，而不考虑这个选择对未来可能产生的影响。这种算法的优点是简单易懂，实现成本低，并且在某些情况下可以获得较好的近似解。但是，贪心算法也存在一定的局限性，它可能无法得到全局最优解。

# 2. Kruskal 算法的理论基础

### 2.1 Kruskal 算法的原理

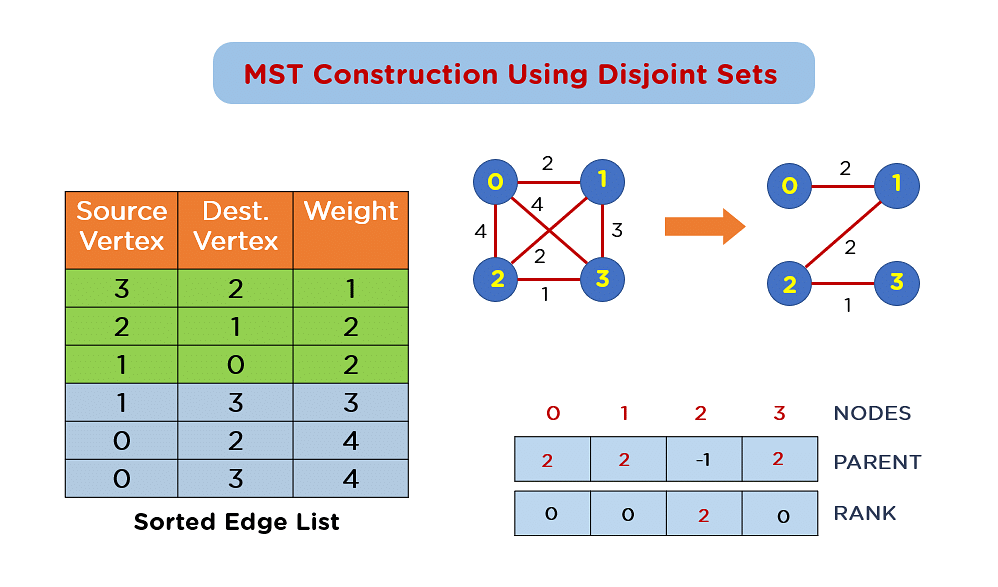
Kruskal 算法是一种贪心算法，用于求解加权无向连通图的最小生成树。它的基本原理是：从图中所有边中，每次选择权值最小的边加入到生成树中，直到生成树包含图中所有顶点。

### 2.2 Kruskal 算法的实现步骤

Kruskal 算法的实现步骤如下：

1. 将图中的所有边按权值从小到大排序。
2. 创建一个并查集数据结构，其中每个顶点最初属于一个单独的集合。
3. 遍历排序后的边：
- 如果边的两个端点属于不同的集合，则将边加入生成树中，并使用并查集将两个集合合并。
- 如果边的两个端点属于同一个集合，则忽略该边。
4. 重复步骤 3，直到生成树包含图中所有顶点。

### 2.3 Kruskal 算法的复杂度分析

Kruskal 算法的时间复杂度为 O(E log E)，其中 E 是图中的边数。

**代码块：**

def kruskal(graph):
  """
  Kruskal 算法求解加权无向连通图的最小生成树。

  参数：
    graph: 加权无向连通图，以邻接表的形式表示。

  返回：
    最小生成树的边集。
  """

  # 初始化并查集
  disjoint_set = DisjointSet()
  for vertex in graph:
    disjoint_set.make_set(vertex)

  # 将边按权值从小到大排序
  edges = sorted(graph.edges(), key=lambda edge: edge.weight)

  # 遍历排序后的边
  mst = set()
  for edge in edges:
    if disjoint_set.find(edge.source) != disjoint_set.find(edge.destination):
      mst.add(edge)
      disjoint_set.union(edge.source, edge.destination)

  return mst

**逻辑分析：**

* `make_set(vertex)` 函数将顶点 `vertex` 初始化为一个单独的集合。
* `find(vertex)` 函数返回包含顶点 `vertex` 的集合的代表元素。
* `union(vertex1, vertex2)` 函数将包含顶点 `vertex1` 和 `vertex2` 的集合合并。
* `sorted(graph.edges(), key=lambda edge: edge.weight)` 将图中的边按权值从小到大排序。
* `mst.add(edge)` 将边 `edge` 加入到最小生成树中。
* `disjoint_set.union(edge.source, edge.destination)` 将包含边 `edge` 两个端点的集合合并。

**参数说明：**

* `graph`：加权无向连通图，以邻接表的形式表示。
* `edge`：图中的边，包含源顶点、目标顶点和权值。

**代码块：**

class DisjointSet:
  """
  并查集数据结构。
  """

  def __init__(self):
    self.parent = {}
    self.rank = {}

  def make_set(self, vertex):
    """
    初始化一个新的集合，包含顶点 `vertex`。

    参数：
      vertex: 顶点。
    """

    self.parent[vertex] = vertex
    self.rank[vertex] = 0

  def find(self, vertex):
    """
    返回包含顶点 `vertex` 的集合的代表元素。

    参数：
      vertex: 顶点。

    返回：
      集合的代表元素。
    """

    if self.parent[vertex] != vertex:
      self.parent[vertex] = self.find(self.parent[vertex])

    return self.parent[vertex]

  def union(self, vertex1, vertex2):
    """
    将包含顶点 `vertex1` 和 `vertex2` 的集合合并。

    参数：
      vertex1: 顶点 1。
      vertex2: 顶点 2。
    """

    root1 = self.find(vertex1)
    root2 = self.find(vertex2)

    if root1 != root2:
      if self.rank[root1] > self.rank[root2]:
        self.parent[root2] = root1
      else:
        self.parent[root1] = root2
        if self.rank[root1] == self.rank[root2]:
          self.rank[root2] += 1

**逻辑分析：**

* `make_set(vertex)` 函数将顶点 `vertex` 初始化为一个单独的集合，其代表元素和秩都为 `vertex`。
* `find(vertex)` 函数使用路径压缩技术递归地查找包含顶点 `vertex` 的集合的代表元素。
* `union(vertex1, vertex2)` 函数使用按秩合并技术将包含顶点