【贪心算法宝典】：原理、应用、实战、陷阱全解析

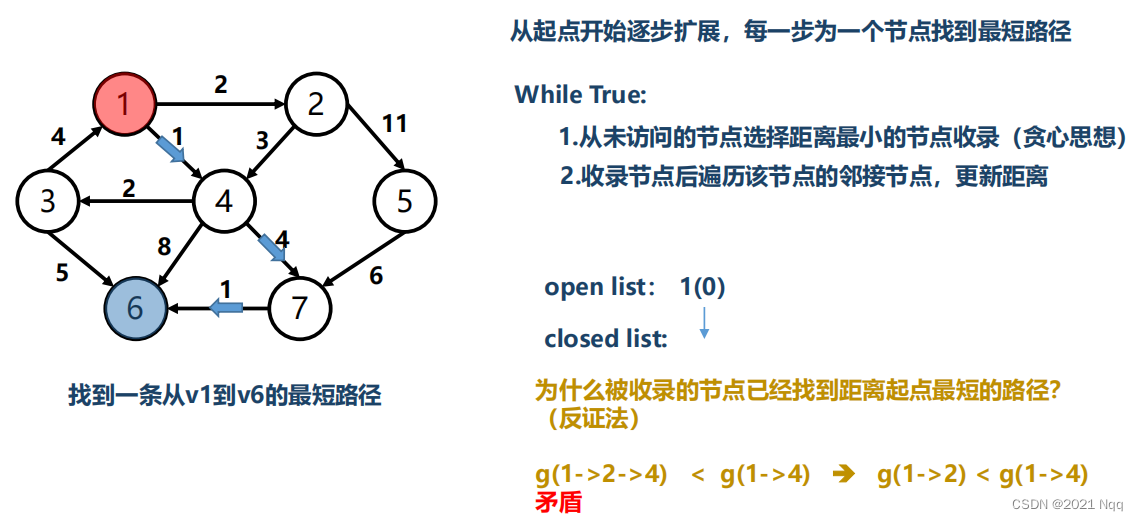
# 1. 贪心算法的理论基础

贪心算法是一种自顶向下的启发式算法，它通过在每个步骤中做出局部最优选择来解决优化问题。其核心思想是：**在当前情况下做出最优选择，而不考虑未来可能的影响。**

贪心算法的优点在于其简单性和效率。它易于理解和实现，并且在许多实际问题中可以快速找到近似最优解。然而，贪心算法也存在局限性，即它可能无法保证找到全局最优解，特别是当问题涉及到负权边或其他特殊情况时。

# 2. 贪心算法的应用场景

贪心算法在实际应用中有着广泛的应用场景，以下列举一些经典的贪心算法实例。

### 2.1 经典贪心算法实例

#### 2.1.1 活动选择问题

**问题描述：**
给定一组活动，每个活动都有一个开始时间和结束时间，要求选择一个不相交的活动子集，使得总活动时间最长。

**贪心算法：**
按照活动结束时间排序，依次选择当前结束时间最早的活动，直到没有活动可选为止。

**代码块：**

def activity_selection(activities):
    """
    贪心算法解决活动选择问题

    Args:
        activities: 活动列表，每个活动是一个元组(start_time, end_time)

    Returns:
        不相交活动子集
    """
    activities.sort(key=lambda x: x[1])  # 按结束时间排序
    selected_activities = []
    last_activity_end_time = -1
    for start_time, end_time in activities:
        if start_time >= last_activity_end_time:
            selected_activities.append((start_time, end_time))
            last_activity_end_time = end_time
    return selected_activities

**逻辑分析：**
1. 将活动按结束时间排序，目的是选择结束时间最早的活动，这样可以最大化后续可选活动的范围。
2. 遍历排序后的活动，如果当前活动的开始时间大于或等于上一个选择的活动的结束时间，则将其加入选择的活动子集中。
3. 每次选择一个活动后，更新上一个选择的活动的结束时间，以避免选择相交的活动。

#### 2.1.2 背包问题

**问题描述：**
给定一个背包容量和一组物品，每个物品都有一个重量和价值，要求选择一个物品子集，使得总重量不超过背包容量，且总价值最大。

**贪心算法：**
按照价值重量比排序，依次选择价值重量比最大的物品，直到背包装满或没有物品可选为止。

**代码块：**

def knapsack(items, capacity):
    """
    贪心算法解决背包问题

    Args:
        items: 物品列表，每个物品是一个元组(weight, value)
        capacity: 背包容量

    Returns:
        选择的物品子集
    """
    items.sort(key=lambda x: x[1] / x[0], reverse=True)  # 按价值重量比排序
    selected_items = []
    current_weight = 0
    for weight, value in items:
        if current_weight + weight <= capacity:
            selected_items.append((weight, value))
            current_weight += weight
        else:
            break
    return selected_items

**逻辑分析：**
1. 将物品按价值重量比排序，目的是选择价值重量比最大的物品，这样可以最大化背包的价值。
2. 遍历排序后的物品，如果当前物品的重量加上背包中已有的重量不超过背包容量，则将其加入选择的物品子集中。
3. 每次选择一个物品后，更新背包中已有的重量，以避免超过背包容量。

#### 2.1.3 最小生成树问题

**问题描述：**
给定一个无向连通图，要求找到一个生成树，使得生成树的边权和最小。

**贪心算法：**
普里姆算法：从一个顶点出发，依次选择权重最小的边，直到生成树包含所有顶点。

**代码块：**

def prim(graph):
    """
    贪心算法解决最小生成树问题（普里姆算法）

    Args:
        graph: 无向连通图，用邻接矩阵表示

    Returns:
        最小生成树的边集
    """
    n = len(graph)
    visited = [False] * n
    visited[0] = True
    edges = []
    while sum(visited) < n:
        min_weight = float('inf')
        min_edge = None
        for i in range(n):
            if visited[i]:
                for j in range(n):
                    if not visited[j] and graph[i][j] > 0 and graph[i][j] < min_weight:
                        min_weight = graph[i][j]
                        min_edge = (i, j)
        if min_edge is not None:
            edges.append(min_edge)
            visited[min_edge[1]] = True
    return edges

**逻辑分析：**
1. 从一个顶点出发，将其标记为已访问。
2. 遍历所有已访问顶点的邻接边，选择权重最小的边，并将其加入生成树中。
3. 将新加入顶点的邻接顶点标记为已访问，重复步骤 2 和 3，直到生成树包含所有顶点。

### 2.2 贪心算法的适用条件

#### 2.2.1 贪心选择性质

贪心算法的本质是每次做出局部最优的选择，即在当前决策下选择最优的选项。如果一个问题满足贪心选择性质，那么贪心算法就有可能找到全局最优解。

#### 2.2.2 最优子结构性质

最优子结构性质是指一个问题的最优解包含其子问题的最优解。如果一个问题满足最优子结构性质，那么贪心算法就有可能找到全局最优解。

# 3.1 贪心算法在调度中的应用

#### 3.1.1 作业调度问题

作业调度问题是指在给定一组作业和一台机器的情况下，如何安排作业的执行顺序，以最小化某种目标函数，如总完成时间或平均等待时间。

**贪心算法的应用：**

贪心算法可以用于解决作业调度问题，其基本思想是每次选择当前最优的作业执行，直到所有作业完成。具体步骤如下：

1. 将作业按某种优先级排序，如最短作业时间优先（SJF）、最短剩余时间优先（SRTF）或最高响应比优先（HRRN）。
2. 从排序后的作业中选择优先级最高的作业执行。
3. 执行该作业，并更新其他作业的剩余时间和等待时间。
4. 重复步骤 2 和 3，直到所有作业完成。

**代码块：**

def greedy_job_scheduling(jobs):
    """
    使用贪心算法解决作业调度问题。

    参数：
        jobs: 作业列表，每个作业包含执行时间和优先级。

    返回：
        总完成时间。
    """

    # 对作业按优先级排序
    jobs.sort(key=lambda job: job.priority, reverse=True)

    # 初始化总完成时间和当前时间
    total_completion_time = 0
    current_time = 0

    # 遍历作业列表
    for job in jobs:
        # 计算作业完成时间
        completion_time = current_time + job.execution_time

        # 更新总完成时间和当前时间
        total_completion_time += completion_time
        current_time = completion_time

    return total_completion_time

**逻辑分析：**

* `greedy_job_scheduling` 函数接收一个作业列表作为输入，每个作业包含执行时间和优先级。
* 函数首先对作业按优先级排序，优先级高的作业排在前面。
* 然后，函数遍历作业列表，每次选择优先级最高的作业执行。
* 函数计算作业的完成时间，并更新总完成时间和当前时间。
* 函数重复执行上述步骤，直到所有作业完成。
* 最后，函数返回总完成时间。

#### 3.1.2 资源分配问题

资源分配问题是指在给定一组资源和一组请求的情况下，如何分配资源以满足请求，同时优化某种目标函数，如总等待时间或资源利用率。

**贪心算法的应用：**

贪心算法可以用于解决资源分配问题，其基本思想是每次分配最能满足当前请求的资源。具体步骤如下：

1. 将请求按某种优先级排序，如最紧急的请求优先或最需要资源的请求优先。
2. 从排序后的请求中选择优先级最高的请求。
3. 为该请求分配最能满足其需求的资源。
4. 更新其他请求的剩余资源需求。
5. 重复步骤 2 和 3，直到所有请求得到满足。

**代码块：**

def greedy_resource_allocation(requests, resources):
    """
    使用贪心算法解决资源分配问题。

    参数：
        requests: 请求列表，每个请求包含所需的资源量。
        resources: 资源列表，每个资源包含可用的资源量。

    返回：
        满足请求所需的总资源量。
    """

    # 对请求按优先级排序
    requests.sort(key=lambda request: request.priority, reverse=True)

    # 初始化总资源量和当前资源量
    total_resources = 0
    current_resources = resources

    # 遍历请求列表
    for request in requests:
        # 计算满足请求所需的资源量
        required_resources = min(request.resources, current_resources)

        # 更新总资源量和当前资源量
        total_resources += required_resources
        current_resources -= required_resources

    return total_resources

**逻辑分析：**

* `greedy_resource_allocation` 函数接收一个请求列表和一个资源列表作为输入，每个请求包含所需的资源量，每个资源包含可用的资源量。
* 函数首先对请求按优先级排序，优先级高的请求排在前面。
* 然后，函数遍历请求列表，每次选择优先级最高的请求。
* 函数计算满足请求所需的资源量，并更新总资源量和当前资源量。
* 函数重复执行上述步骤，直到所有请求得到满足。
* 最后，函数返回满足请求所需的总资源量。

# 4. 贪心算法的陷阱和应对

### 4.1 贪心算法的局限性

贪心算法虽然简单易懂，但在某些情况下，它可能会陷入陷阱，导致无法获得全局最优解。

#### 4.1.1 局部最优与全局最优

贪心算法的本质是基于局部最优选择，即在每一步选择当前最优的方案。然而，这种局部最优选择并不总是能保证全局最优。

**示例：**活动选择问题中，如果贪心选择每次选择时间段最长的活动，则可能无法得到总时间最长的活动安排。

#### 4.1.2 负权边问题

贪心算法通常假设问题中的权重都是非负的。然而，当存在负权边时，贪心算法可能会陷入死循环，无法找到最优解。

**示例：**最短路径问题中，如果存在负权边，则贪心选择每次选择权重最小的边可能无法找到最短路径。

### 4.2 应对贪心算法陷阱的方法

为了应对贪心算法的陷阱，可以采取以下方法：

#### 4.2.1 证明贪心算法的正确性

对于某些贪心算法，可以通过数学证明来证明其在特定条件下的正确性。例如，对于活动选择问题，可以通过数学归纳法证明贪心算法总是能得到最优解。

#### 4.2.2 使用其他优化算法

当贪心算法无法满足要求时，可以考虑使用其他优化算法，例如动态规划、分支限界法等。这些算法虽然复杂度更高，但可以保证找到全局最优解。

**示例：**对于背包问题，当物品价值和重量较大时，贪心算法可能无法找到最优解，可以使用动态规划算法来解决。

#### 4.2.3 负权边问题应对策略

对于负权边问题，可以采用以下策略：

- **Bellman-Ford 算法：**该算法可以处理负权边，但时间复杂度较高。
- **Dijkstra 算法：**该算法不能处理负权边，但时间复杂度较低。可以先使用 Dijkstra 算法找到最短路径，然后检查是否存在负权环，如果存在则说明没有最短路径。

#### 4.2.4 证明贪心算法的正确性示例

**活动选择问题贪心算法正确性证明：**

**引理：**如果活动 i 和 j 不冲突，则贪心算法选择活动 i 后，再选择活动 j 总是最优的。

**证明：**

假设贪心算法选择活动 i 后，再选择活动 k（k != j）。由于 i 和 j 不冲突，因此 i 和 k 也一定不冲突。

如果选择 k 比选择 j 更优，则 k 的结束时间必须晚于 j 的结束时间。但是，贪心算法在选择活动 i 后，会优先选择结束时间最早的活动，因此 k 的结束时间不可能晚于 j 的结束时间。

因此，引理成立。

**贪心算法正确性证明：**

根据引理，如果贪心算法选择活动 i，则贪心算法选择活动 i 后再选择活动 j 总是最优的。

因此，贪心算法选择活动 i，再选择活动 j，再选择活动 k，...，直到选择所有活动，总是最优的。

因此，贪心算法总是能得到最优解。

# 5.1 贪心算法的变种

### 5.1.1 近似贪心算法

近似贪心算法是一种贪心算法的变种，它允许在某些情况下做出次优选择，以获得更好的整体解决方案。与传统的贪心算法相比，近似贪心算法在某些情况下可以找到更接近全局最优解的解。

**应用场景：**

近似贪心算法常用于解决 NP 难问题，这些问题通常无法在多项式时间内找到最优解。通过允许做出次优选择，近似贪心算法可以在可接受的时间内找到近似最优解。

**代码示例：**

def approximate_greedy(problem):
    """
    近似贪心算法

    参数：
        problem：问题实例

    返回：
        近似最优解
    """

    # 初始化近似最优解
    best_solution = None

    # 遍历所有可能的解
    for solution in problem.solutions:
        # 计算解的近似值
        approximation = problem.approximate_value(solution)

        # 如果当前解的近似值优于最佳解，则更新最佳解
        if approximation > problem.approximate_value(best_solution):
            best_solution = solution

    # 返回近似最优解
    return best_solution

### 5.1.2 分治贪心算法

分治贪心算法是一种贪心算法的变种，它将问题分解为更小的子问题，然后递归地应用贪心算法解决子问题。与传统的贪心算法相比，分治贪心算法可以提高某些问题的求解效率。

**应用场景：**

分治贪心算法常用于解决具有分治结构的问题，例如区间调度问题和线段覆盖问题。通过将问题分解为更小的子问题，分治贪心算法可以有效地利用子问题的最优解来构造全局最优解。

**代码示例：**

def divide_and_conquer_greedy(problem):
    """
    分治贪心算法

    参数：
        problem：问题实例

    返回：
        最优解
    """

    # 如果问题规模较小，则直接解决
    if problem.size < threshold:
        return problem.solve()

    # 分解问题为更小的子问题
    subproblems = problem.decompose()

    # 递归地解决子问题
    subproblem_solutions = [divide_and_conquer_greedy(subproblem) for subproblem in subproblems]

    # 合并子问题的解
    return problem.combine(subproblem_solutions)

# 6.1 贪心算法的优势和劣势

贪心算法具有以下优势：

- **简单易懂：**贪心算法的思想简单易懂，实现起来也相对容易。
- **效率高：**贪心算法通常具有较高的时间复杂度，在处理大规模数据时效率较高。
- **局部最优性：**贪心算法在每次选择时都做出局部最优的选择，这使得算法在某些情况下可以快速找到近似最优解。

然而，贪心算法也存在一些劣势：

- **全局最优性：**贪心算法的局部最优性可能导致算法无法找到全局最优解。
- **负权边问题：**当权重为负时，贪心算法可能无法得到正确的结果。
- **适用场景受限：**贪心算法只适用于满足特定条件的问题，在其他情况下可能无法有效解决问题。

## 6.2 贪心算法的未来发展趋势

贪心算法在未来仍具有广阔的发展前景，主要体现在以下几个方面：

- **理论研究：**对贪心算法的理论基础进行更深入的研究，探索新的贪心算法变种和适用场景。
- **算法优化：**通过改进贪心算法的实现方式和优化策略，提高算法的效率和准确性。
- **应用拓展：**将贪心算法应用到更多领域，例如人工智能、大数据分析和运筹优化等。