探索无向图匹配问题：揭开图论配对奥秘的本质

# 1. 无向图匹配问题的基础理论

无向图匹配问题是图论中一个基本问题，它涉及在给定的无向图中寻找具有特定性质的匹配。匹配是指图中边的一个集合，其中任何两个边都不共享一个公共顶点。

无向图匹配问题的基础理论包括以下几个关键概念：

- **最大匹配：**给定一个无向图，最大匹配是指边数最多的匹配。
- **最小覆盖：**给定一个无向图，最小覆盖是指包含图中所有顶点的边数最少的边集合。
- **完美匹配：**给定一个无向图，完美匹配是指一个匹配，其中图中的每个顶点都与其他顶点相匹配。

# 2. 无向图匹配算法的实践应用

无向图匹配算法在现实世界中有着广泛的应用，从社交网络分析到资源分配问题。本章节将深入探讨两种重要的无向图匹配算法：最大匹配算法和最小覆盖算法。

### 2.1 最大匹配算法

最大匹配算法的目标是找到无向图中最大的匹配，即图中最大数量的非相交边。最大匹配算法有两种主要类型：匈牙利算法和Edmonds-Karp算法。

#### 2.1.1 匈牙利算法

匈牙利算法是一种基于增广路径的贪心算法。它从一个空匹配开始，并迭代地查找增广路径，即从未匹配的顶点到未匹配的顶点的路径，其中路径上的所有边都已匹配。如果找到增广路径，则算法将沿着该路径交替匹配和取消匹配边，直到找到最大匹配。

def hungarian_algorithm(graph):
    """
    使用匈牙利算法求解最大匹配。

    参数：
        graph: 无向图，表示为邻接矩阵。

    返回：
        最大匹配。
    """
    n = len(graph)
    matching = [None] * n

    # 初始化标签
    labels = [0] * n
    for i in range(n):
        for j in range(n):
            if graph[i][j] > labels[i]:
                labels[i] = graph[i][j]

    # 主循环
    while True:
        # 寻找增广路径
        path = find_augmenting_path(graph, matching, labels)
        if path is None:
            break

        # 沿着增广路径交替匹配和取消匹配边
        for i, j in path:
            if matching[i] is None:
                matching[i] = j
            else:
                matching[matching[i]] = None
                matching[i] = j

    return matching

#### 2.1.2 Edmonds-Karp算法

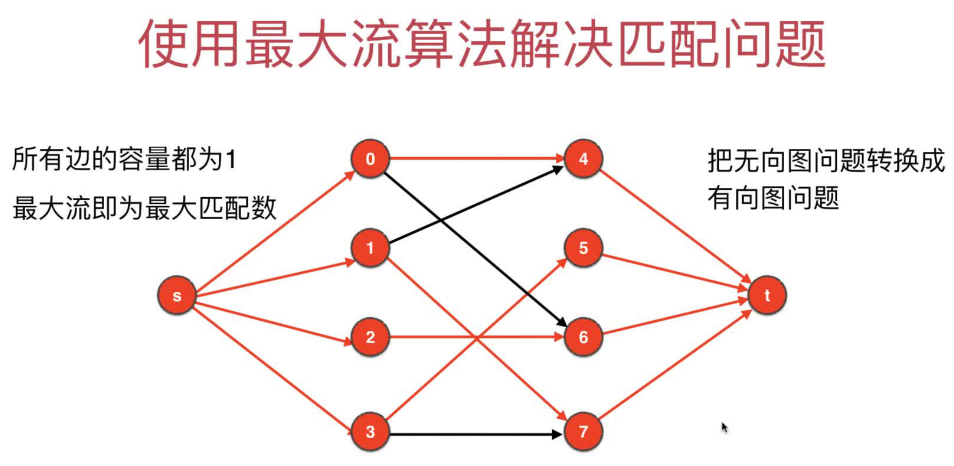
Edmonds-Karp算法是一种基于最大流的算法。它将无向图转换为一个有向图，并使用最大流算法来找到最大匹配。最大流算法的工作原理是将流量推送到网络中，直到无法再增加流量为止。

def edmonds_karp_algorithm(graph):
    """
    使用Edmonds-Karp算法求解最大匹配。

    参数：
        graph: 无向图，表示为邻接矩阵。

    返回：
        最大匹配。
    """
    n = len(graph)
    residual_graph = [[0] * n for _ in range(n)]
    for i in range(n):
        for j in range(n):
            residual_graph[i][j] = graph[i][j]

    # 寻找增广路径
    while True:
        path = find_augmenting_path(residual_graph)
        if path is None:
            break

        # 沿着增广路径增加流量
        flow = min(residual_graph[path[i]][path[i+1]] for i in range(len(path)-1))
        for i in range(len(path)-1):
            residual_graph[path[i]][path[i+1]] -= flow
            residual_graph[path[i+1]][path[i]] += flow

    # 提取最大匹配
    matching = [None] * n
    for i in range(n):
        for j in range(n):
            if residual_graph[i][j] == 0 and graph[i][j] > 0:
                matching[i] = j

    return matching

### 2.2 最小覆盖算法

最小覆盖算法的目标是找到无向图中的最小覆盖，即图中最小数量的边，使得每个顶点都与至少一条边相连。最小覆盖算法有两种主要类型：König定理和Ford-Fulkerson算法。

#### 2.2.1 König定理

König定理指出，无向图中的最小覆盖和最大匹配的大小相等。因此，可以使用最大匹配算法来求解最小覆盖。

#### 2.2.2 Ford-Fulkerson算法

Ford-Fulkerson算法是一种基于最大流的算法。它将无向图转换为一个有向图，并使用最大流算法来找到最小覆盖。最大流算法的工作原理是将流量推送到网络中，直到无法再增加流量为止。

def ford_fulkerson_algorit