探索无向图强连通分量：深入理解图论强连通性的本质

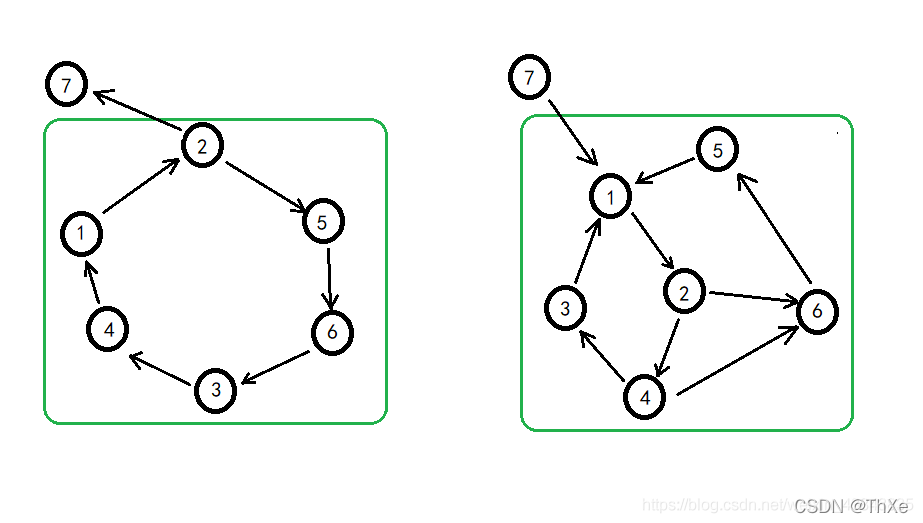
# 1. 无向图强连通分量概述

无向图中的强连通分量是指图中的一组顶点，它们之间可以相互到达。换句话说，强连通分量中的任何两个顶点之间都存在一条路径。强连通分量是无向图中一个重要的概念，它可以用于解决各种问题，例如社区划分、网络分析和数据挖掘。

# 2. 强连通分量的理论基础

### 2.1 强连通分量的定义和性质

**定义：**

无向图 G 中的强连通分量（Strongly Connected Component，简称 SCC）是指图中的一组顶点，满足以下条件：

* **强连通性：**组内任意两个顶点之间都存在一条路径。
* **极大性：**组内不存在任何其他顶点可以加入而仍保持强连通性。

**性质：**

* **等价类：**强连通分量是无向图 G 的等价类，即图中顶点的划分，使得同属一个强连通分量的顶点等价，不同强连通分量的顶点不等价。
* **唯一性：**每个顶点只属于一个强连通分量。
* **导出子图：**强连通分量形成的导出子图是一个强连通图。

### 2.2 强连通分量分解定理

**定理：**

任意一个无向图 G 可以唯一分解为若干个强连通分量，且这些强连通分量两两不相交。

**证明：**

* **存在性：**从图 G 中任选一个顶点 v，使用深度优先搜索（DFS）遍历从 v 出发的所有可达顶点，得到一个强连通分量。重复此过程，直到遍历完所有顶点，即可得到图 G 的所有强连通分量。
* **唯一性：**假设存在两个不同的强连通分量 C1 和 C2，则 C1 中存在顶点 v1，C2 中存在顶点 v2，使得 v1 可达 v2 或 v2 可达 v1。这与强连通分量的定义矛盾，因此强连通分量分解是唯一的。

### 2.3 强连通分量图的性质

强连通分量图（SCC 图）是由强连通分量组成的有向图，其中：

* **顶点：**每个顶点代表一个强连通分量。
* **边：**如果强连通分量 C1 中存在顶点 v1，强连通分量 C2 中存在顶点 v2，且 v1 可达 v2，则 SCC 图中存在一条从 C1 到 C2 的有向边。

**性质：**

* **无环：**SCC 图是一个无环图，因为强连通分量之间不存在环。
* **连通：**SCC 图是一个连通图，因为任意两个强连通分量之间都存在路径。
* **拓扑排序：**SCC 图可以进行拓扑排序，排序结果表示强连通分量的线性序。

# 3. 强连通分量的算法实现

### 3.1 Kosaraju算法

#### 3.1.1 Kosaraju算法原理

Kosaraju算法是一种基于深度优先搜索（DFS）的算法，用于计算有向图中的强连通分量。该算法分为两个阶段：

1. **逆后序DFS阶段：**从图的任意一个顶点出发，对图进行DFS，记录每个顶点的出栈顺序。
2. **正序DFS阶段：**将图中的所有边反向，从出栈顺序最大的顶点出发，对反向图进行DFS，形成的连通子图即为一个强连通分量。

#### 3.1.2 Kosaraju算法步骤

1. **逆后序DFS阶段：**
- 从图的任意一个顶点出发，进行DFS。
- 当一个顶点的所有邻接顶点都已访问过时，将该顶点压入栈中。
- 重复步骤2，直到所有顶点都已访问过。

2. **正序DFS阶段：**
- 将图中的所有边反向。
- 从出栈顺序最大的顶点出发，进行DFS。
- 形成的连通子图即为一个强连通分量。
- 重复步骤3，直到所有顶点都已访问过。

**代码块：**

def kosaraju(graph):
    """
    Kosaraju算法计算有向图中的强连通分量。

    参数：
        graph: 有向图，表示为邻接表。

    返回：
        强连通分量的列表。
    """

    # 逆后序DFS阶段
    stack = []
    visited = set()

    def dfs1(node):
        if node in visited:
            return
        visited.add(node)
        for neighbor in graph[node]:
            dfs1(neighbor)
        stack.append(node)

    for node in graph:
        d