破解无向图着色问题：解锁图论染色难题的奥秘

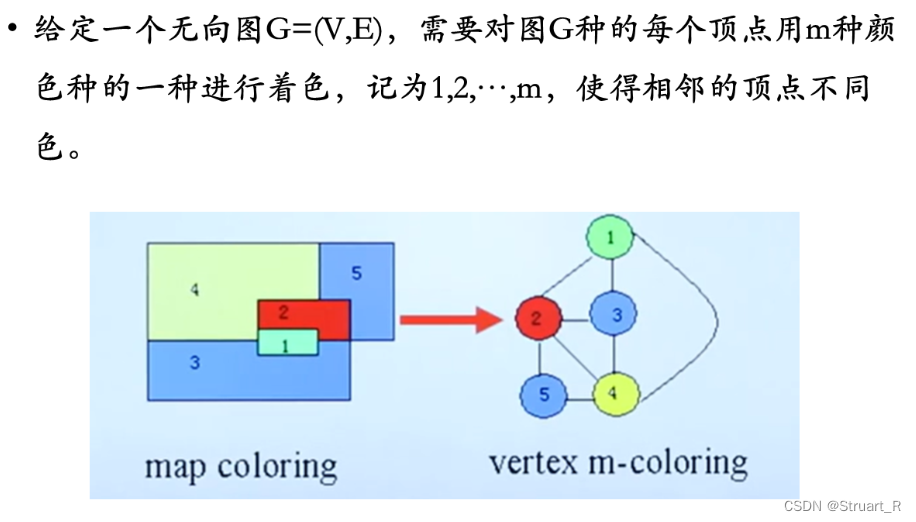
# 1. 无向图着色的基本概念**

无向图着色问题是图论中一个经典问题，其目的是为给定无向图中的每个顶点分配一种颜色，使得相邻顶点具有不同的颜色。无向图着色在现实世界中有着广泛的应用，例如冲突调度和地图着色。

**定义：**
* 无向图：一个由顶点和边组成的数学结构，其中边连接顶点，但没有方向。
* 着色：为图中每个顶点分配一种颜色，使得相邻顶点具有不同的颜色。
* 色数：为给定图着色所需的最少颜色数。
* 可染色性：一个图是否可以被着色。

# 2. 无向图着色的理论基础

### 2.1 图论染色理论

#### 2.1.1 色数和可染色性

**色数**是指给定无向图着色所需的最小颜色数。一个无向图的可染色性由其色数决定。

**可染色性定理：**一个无向图是可染色的，当且仅当它不包含奇环。

**证明：**

* **充分性：**如果一个无向图不包含奇环，则可以通过以下步骤着色：
* 从任意顶点开始，用颜色 1 着色。
* 对于每个未着色的顶点，选择一个与其相邻顶点不同的颜色着色。
* 由于没有奇环，因此总能找到一个颜色来着色每个顶点。

* **必要性：**如果一个无向图包含奇环，则它不可染色。这是因为奇环中的每个顶点都必须着色为不同的颜色，因此需要至少奇环长度的颜色。

#### 2.1.2 着色多项式

**着色多项式**是一个多项式，它表示一个无向图的所有合法着色的数量。它可以用来计算无向图的色数。

**着色多项式定理：**一个无向图 G 的着色多项式 P(G, x) 是一个 x 次多项式，其中 x 表示着色的颜色数。P(G, x) 的根是 G 的所有合法着色的色数。

### 2.2 着色算法的复杂性分析

#### 2.2.1 NP完全性

无向图着色问题是一个 **NP完全** 问题，这意味着：

* **NP：**给定一个着色方案，可以在多项式时间内验证其是否合法。
* **完全：**任何其他 NP 问题都可以通过多项式时间归约转换为无向图着色问题。

NP完全性表明无向图着色问题在计算上是困难的，对于大规模图，找到最优解可能非常耗时。

#### 2.2.2 近似算法

由于无向图着色问题的 NP完全性，研究人员开发了近似算法来找到近似最优解。近似算法保证找到的解的质量与最优解相比不会太差。

**常见的近似算法：**

* **贪心算法：**在每个步骤中，选择一个最难着色的顶点并为其分配一个颜色。
* **回溯算法：**尝试所有可能的着色方案，并保存找到的最佳方案。
* **局部搜索算法：**从一个初始着色方案开始，并逐步调整着色以改善解决方案。

# 3. 无向图着色的实践算法**

### 3.1 贪心算法

贪心算法是一种基于局部最优选择策略的算法，它在每个步骤中都做出局部最优的选择，以期得到全局最优解。在无向图着色问题中，贪心算法可以用于为图中的顶点分配颜色，使得相邻顶点具有不同的颜色。

#### 3.1.1 邻接度着色

邻接度着色算法是一种贪心算法，它按照顶点的邻接度进行着色。邻接度是指一个顶点与其他顶点相邻的边数。算法首先对顶点按照邻接度降序排序，然后依次为每个顶点分配一个颜色，使得该顶点与已着色的相邻顶点具有不同的颜色。

def adjacent_degree_coloring(graph):
    """
    邻接度着色算法

    参数：
        graph: 无向图，表示为邻接表

    返回：
        color_map: 顶点到颜色的映射
    """

    # 对顶点按照邻接度降序排序
    vertices = sorted(graph.vertices, key=lambda v: -v.degree)

    # 初始化颜色映射
    color_map = {}

    # 遍历顶点
    for vertex in vertices:
        # 获取已着色的相邻顶点的颜色集合
        used_colors = set(color_map[neighbor] for neighbor in vertex.neighbors if neighbor in color_map)

        # 为顶点分配一个未使用的颜色
        for color in range(1, graph.num_vertices + 1):
            if color not in used_colors:
                color_map[vertex] = color
                break

    return color_map

**代码逻辑分析：**

1. `sorted(graph.vertices, key=lambda v: -v.degree)`：对顶点按照邻接度降序排序。
2. `used_colors = set(color_map[neighbor] for neighbor in vertex.neighbors if neighbor in color_map)`：获取已着色的相邻顶点的颜色集合。
3. `for color in range(1, graph.num_vertices + 1):`：遍历所有可能的颜色。
4. `if color not in used_colors:`：如果当前颜色未被相邻顶点使用，则为顶点分配该颜色。

#### 3.1.2 最大度着色

最大度着色算法也是一种贪心算法，它按照顶点的最大度进行着色。最大度是指一个顶点与其他顶点相邻的边数中最大的一个。算法首先对顶点按照最大度降序排序，然后依次为每个顶点分配一个颜色，使得该顶点与已着色的相邻顶点具有不同的颜色。

def maximum_degree_coloring(graph):
    """
    最大度着色算法

    参数：
        graph: 无向图，表示