神经网络训练机制：反向传播算法的3个关键步骤

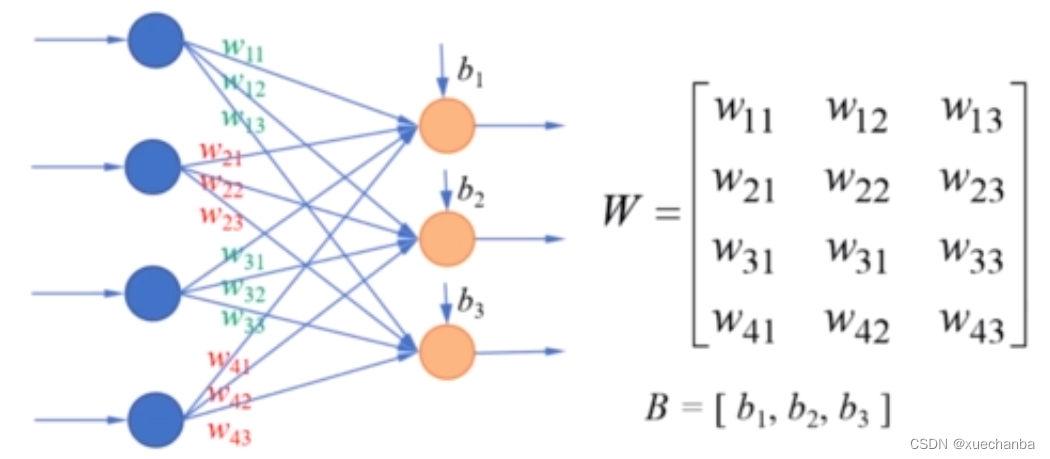
# 1. 神经网络训练概述

神经网络训练是机器学习中至关重要的一步，它通过反向传播算法来调整网络权重，以最小化损失函数并提高模型性能。反向传播算法是一种梯度下降算法，它计算损失函数相对于权重的梯度，并使用这些梯度来更新权重，从而使损失函数最小化。

反向传播算法的数学基础是链式法则，它允许我们计算复杂函数的梯度，例如神经网络的损失函数。通过应用链式法则，我们可以计算损失函数相对于每个权重的梯度，并使用这些梯度来更新权重。

# 2. 反向传播算法的理论基础

### 2.1 反向传播算法的原理和数学推导

#### 2.1.1 误差函数和梯度下降法

反向传播算法的目标是通过最小化误差函数来训练神经网络。误差函数衡量了模型预测与真实标签之间的差异。常用的误差函数包括均方误差（MSE）和交叉熵损失。

梯度下降法是一种优化算法，用于找到误差函数的最小值。它通过迭代更新模型参数的方向来实现，每次更新的方向由误差函数的梯度决定。

#### 2.1.2 反向传播算法的链式法则求导

反向传播算法使用链式法则来计算误差函数对模型参数的梯度。链式法则允许将复杂函数的梯度分解为较小函数梯度的乘积。

设 `f` 为误差函数，`x` 为模型参数，则 `f` 对 `x` 的梯度为：

∇f(x) = ∂f/∂x

如果 `f` 是由一系列函数 `g`、`h`、...、`z` 组成，即：

f = g(h(z))

则 `f` 对 `x` 的梯度可以分解为：

∇f(x) = ∂f/∂g * ∂g/∂h * ∂h/∂z * ... * ∂z/∂x

反向传播算法通过从输出层向输入层逐层反向计算每个函数的梯度，从而计算误差函数对模型参数的梯度。

### 2.2 反向传播算法的变种

#### 2.2.1 动量法和 RMSProp

动量法和 RMSProp 是反向传播算法的变种，它们通过引入动量和自适应学习率来加速训练过程。

动量法通过对梯度进行加权平均来更新模型参数，从而减少训练过程中的震荡。RMSProp 通过对历史梯度平方进行加权平均来调整学习率，从而使学习率适应不同的模型参数。

#### 2.2.2 Batch Normalization 和 Dropout

Batch Normalization 和 Dropout 是正则化技术，它们可以帮助防止神经网络过拟合。

Batch Normalization 通过将每个批次的数据归一化到均值 0 和方差 1 来减少内部协变量偏移。Dropout 通过随机丢弃神经元来减少模型对特定特征的依赖性。

# 3. 反向传播算法的实践应用

### 3.1 反向传播算法在分类任务中的应用

反向传播算法在分类任务中有着广泛的应用，例如图像分类、文本分类和语音识别。在这些任务中，模型需要学习将输入数据映射到一组离散的类别。

#### 3.1.1 训练一个多层感知机分类器

多层感知机（MLP）是一种前馈神经网络，广泛用于分类任务。MLP由输入层、隐藏层和输出层组成。输入层接收输入数据，隐藏层执行非线性变换，输出层输出预测的类别。

import numpy as np
import tensorflow as tf

# 创建一个 MLP 分类器
model = tf.keras.Sequential([
  tf.keras.layers.Dense(units=128, activation='relu', input_shape=(784,)),
  tf.keras.layers.Dense(units=10, activation='softmax')
])

# 编译模型
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])

# 训练模型
model.fit(x_train, y_train, epochs=10)

# 评估模型
model.evaluate(x_test, y_test)

**代码逻辑分析：**

* `model.compile()`：编译模型，指定优化器、损失函数和评估指标。
* `model.fit()`：训练模型，指定训练数据和训练轮数。
* `model.evaluate()`：评估模型，指定测试数据。

**参数说明：**

* `units`：隐藏层和输出层的神经元数量。
* `activation`：隐藏层和输出层的激活函数。
* `input_shape`：输入数据的形状。
* `optimizer`：优化算法。
* `loss`：损失函数。
* `metrics`：评估指标。
* `epochs`：训练轮数。

#### 3.1.2 优化超参数和评估模型性能

训练一个 MLP 分类器时，需要优化超参数，如学习率、隐藏层数量和神经元数量。可以使用交叉验证或网格搜索等技术来优化超参数。

模型性能可以通过准确率、召回率和 F1 分数等指标来评估。此外，还可以使用混淆矩阵来分析模型的预测结果。

### 3.2 反向传播算法在回归任务中的应用

反向传播算法也可用于回归任务，例如预测连续值。在回归任务中，模型需要学习将输入数据映射到一个连续的输出值。

#### 3.2.1 训练一个线性回归模型

线性回归是一种简单的回归模型，用于预测连续变量之间的线性关系。线性回归模型由一个权重向量和一个偏置项组成。

import numpy as np
import tensorflow as tf

# 创建一个线性回归模型
model = tf.keras.Sequential([
  tf.keras.layers.Dense(units=1, input_shape=(1,))
])

# 编译模型
model.compile(optimizer='adam', loss='mean_squared_error')

# 训练模型
model.fit(x_train, y_train, epochs=100)

# 评估模型
model.evaluate(x_test, y_test)

**代码逻辑分析：**

* `model.compile()`：编译模型，指定优化器和损失函数。
* `model.fit()`：训练模型，指定训练数据和训练轮数。
* `model.evaluate()`：评估模型，指定测试数据。

**参数说明：**

* `units`：输出层的节点数。
* `input_shape`：输入数据的形状。
* `optimizer`：优化算法。
* `loss`：损失函数。
* `epochs`：训练轮数。

#### 3.2.2 处理非线性回归问题

对于非线性回归问题，可以使用神经网络来拟合复杂的关系。例如，可以使用多层感知机或卷积神经网络来处理非线性回归问题。

import numpy as np
import tensorflow as tf

# 创建一个 MLP 回归模型
model = tf.keras.Sequential([
  tf.keras.layers.Dense(units=128, activation='relu', input_shape=(1,)),
  tf.keras.layers.Dense(units=1)
])

# 编译模型
model.compile(optimizer='adam', loss='mean_squared_error')

# 训练模型
model.fit(x_train, y_train, epochs=100)

# 评估模型
model.evaluate(x_test, y_test)

**代码逻辑分析：**

* `model.compile()`：编译模型，指定优化器和损失函数。
* `model.fit()`：训练模型，指定训练数据和训练轮数。
* `model.evaluate()`：评估模型，指定测试数据。

**参数说明：**

* `units`：隐藏层和输出层的节点数。
* `activation`：隐藏层的激活函数。
* `input_shape`：输入数据的形状。
* `optimizer`：优化算法。
* `loss`：损失函数。
* `epochs`：训练轮数。

# 4. 反向传播算法的进阶应用

### 4.1 反向传播算法在卷积神经网络中的应用

#### 4.1.1 卷积神经网络的结构和原理

卷积神经网络（CNN）是一种深度神经网络，专为处理具有网格状结构的数据（例如图像）而设计。CNN 的基本组成部分是卷积层和池化层。

**卷积层**应用一系列滤波器（也称为内核）对输入数据进行卷积操作。每个滤波器在输入数据上滑动，计算其元素与滤波器元素的逐元素乘积的总和。卷积操作可以检测输入数据中的局部模式和特征。

**池化层**对卷积层的输出进行降采样，以减少数据维度并提高计算效率。池化操作通常使用最大池化或平均池化。最大池化取一个局部区域中的最大值，而平均池化取平均值。

#### 4.1.2 反向传播算法在卷积层和池化层的应用

在卷积神经网络中，反向传播算法用于计算每个参数的梯度。对于卷积层，梯度计算涉及以下步骤：

1. **前向传播：**计算卷积层的输出。
2. **反向传播：**计算误差函数相对于卷积层输出的梯度。
3. **卷积反向传播：**应用链式法则，将误差梯度传播到卷积层输入和滤波器权重。

对于池化层，梯度计算涉及以下步骤：

1. **前向传播：**计算池化层的输出。
2. **反向传播：**计算误差函数相对于池化层输出的梯度。
3. **池化反向传播：**根据池化操作的类型（最大池化或平均池化），将误差梯度传播到池化层输入。

### 4.2 反向传播算法在循环神经网络中的应用

#### 4.2.1 循环神经网络的结构和原理

循环神经网络（RNN）是一种深度神经网络，专为处理序列数据（例如文本或时间序列）而设计。RNN 的基本组成部分是循环单元，它可以记住先前输入的信息。

**循环单元**在每个时间步接收输入并输出一个隐藏状态。隐藏状态包含有关序列中先前输入的信息。RNN 通过将隐藏状态馈送到下一个循环单元来处理序列数据。

#### 4.2.2 反向传播算法在 LSTM 和 GRU 中的应用

长短期记忆（LSTM）和门控循环单元（GRU）是两种流行的 RNN 单元。它们使用门控机制来控制信息流，从而提高 RNN 处理长期依赖关系的能力。

在 LSTM 和 GRU 中，反向传播算法用于计算每个参数的梯度。梯度计算涉及以下步骤：

1. **前向传播：**计算 LSTM 或 GRU 单元的输出。
2. **反向传播：**计算误差函数相对于 LSTM 或 GRU 单元输出的梯度。
3. **循环反向传播：**应用链式法则，将误差梯度传播到 LSTM 或 GRU 单元输入和门控权重。

# 5.1 反向传播算法的并行化

反向传播算法的计算量很大，尤其是对于大型神经网络。为了提高训练效率，可以采用并行化技术。

### 5.1.1 数据并行和模型并行

数据并行是一种并行化技术，它将训练数据分成多个子集，并在不同的设备（例如 GPU）上并行处理。每个设备负责计算一个子集上的梯度，然后将梯度聚合起来更新模型参数。

模型并行是一种并行化技术，它将模型分成多个子模型，并在不同的设备上并行处理。每个设备负责计算一个子模型上的梯度，然后将梯度聚合起来更新模型参数。

### 5.1.2 分布式训练和 GPU 加速

分布式训练是一种并行化技术，它将训练任务分布在多台机器上。每台机器负责计算一部分梯度，然后将梯度聚合起来更新模型参数。

GPU 加速是一种并行化技术，它利用 GPU 的并行计算能力来加速训练过程。GPU 具有大量的并行处理单元，可以同时执行大量的计算。

**代码示例：**

import torch
import torch.nn as nn
import torch.optim as optim
import torch.distributed as dist

# 初始化分布式训练环境
dist.init_process_group(backend="nccl")

# 创建模型
model = nn.Linear(100, 10)

# 将模型分布到不同的 GPU 设备上
model = nn.DataParallel(model)

# 创建优化器
optimizer = optim.SGD(model.parameters(), lr=0.01)

# 训练模型
for epoch in range(10):
    # 将数据分成子集
    data_sublists = torch.chunk(data, dist.get_world_size())

    # 在不同的设备上并行计算梯度
    for data_sublist in data_sublists:
        optimizer.zero_grad()
        output = model(data_sublist)
        loss = torch.nn.MSELoss()(output, target)
        loss.backward()

    # 聚合梯度
    dist.all_reduce(model.parameters())

    # 更新模型参数
    optimizer.step()

**逻辑分析：**

这段代码使用 PyTorch 的分布式训练功能来实现数据并行。它将数据分成子集，并在不同的 GPU 设备上并行计算梯度。然后，它将梯度聚合起来更新模型参数。

**参数说明：**

* `dist.init_process_group(backend="nccl")`：初始化分布式训练环境，使用 NCCL 后端。
* `model = nn.DataParallel(model)`：将模型分布到不同的 GPU 设备上。
* `optimizer = optim.SGD(model.parameters(), lr=0.01)`：创建优化器，使用 SGD 算法和学习率为 0.01。
* `for epoch in range(10)`：训练模型 10 个 epoch。
* `data_sublists = torch.chunk(data, dist.get_world_size())`：将数据分成子集。
* `for data_sublist in data_sublists`：在不同的设备上并行计算梯度。
* `dist.all_reduce(model.parameters())`：聚合梯度。
* `optimizer.step()`：更新模型参数。

# 6. 反向传播算法的局限性和未来发展

### 6.1 反向传播算法的局限性

反向传播算法虽然在神经网络训练中取得了巨大的成功，但它也存在一些固有的局限性：

#### 6.1.1 局部最优和鞍点问题

反向传播算法是一个基于梯度下降的优化算法，它可能会陷入局部最优或鞍点。局部最优是指一个非全局最优解，而鞍点是指一个函数值既不是最大值也不是最小值，而是介于两者之间的点。当反向传播算法遇到局部最优或鞍点时，它可能无法找到全局最优解，从而导致模型性能不佳。

#### 6.1.2 过拟合和欠拟合问题

反向传播算法容易出现过拟合和欠拟合问题。过拟合是指模型在训练数据集上表现良好，但在新数据上表现不佳，而欠拟合是指模型在训练和新数据上都表现不佳。过拟合通常是由于模型过于复杂，而欠拟合通常是由于模型过于简单。

### 6.2 反向传播算法的未来发展

为了克服反向传播算法的局限性，研究人员正在探索各种新的优化算法和超参数调优技术。这些技术包括：

#### 6.2.1 新型优化算法和超参数调优技术

* **自适应学习率优化器：**这些优化器可以自动调整学习率，从而避免陷入局部最优或鞍点。
* **正则化技术：**正则化技术可以防止模型过拟合，例如 L1 正则化、L2 正则化和 Dropout。
* **超参数调优技术：**超参数调优技术可以帮助找到最佳的超参数组合，例如学习率、批次大小和网络架构。

#### 6.2.2 可解释性和可信赖性研究

除了优化算法的改进之外，研究人员还关注反向传播算法的可解释性和可信赖性。可解释性是指了解模型如何做出决策，而可信赖性是指对模型预测的置信度。这些研究领域对于提高神经网络的可靠性和透明度至关重要。